3.1 Definition of the Derivative
We begin with two questions: What is the precise definition of a tangent line? And how can we compute its slope? To answer these questions, let’s return to the relationship between tangent and secant lines first mentioned in Section 2.1.
The secant line through distinct points \(P = (a, f(a))\) and \(Q = (x, f(x))\) on the graph of a function \(f(x)\) has slope [Figure 3.1(A)]
\[\frac{\Delta f}{\Delta x} = \frac{f(x) - f(a)}{x-a}\]
where
\[\Delta f = f(x) - f(a)\text{ and }\Delta x = x - a\]
REMINDER A secant line is any line through two points on a curve or graph.
The expression \(\dfrac{f(x) - f(a)}{x-a}\) is called the difference quotient.
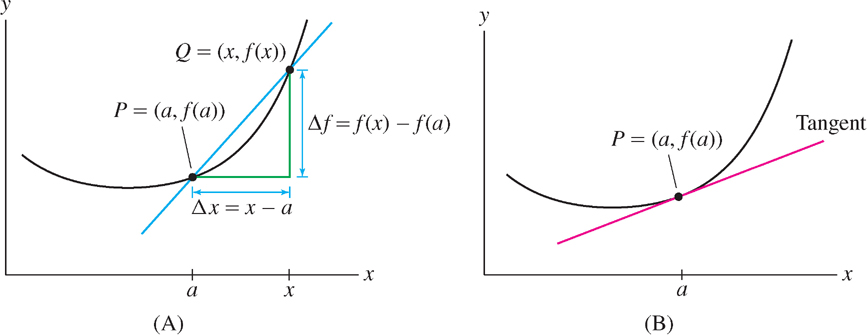
Now observe what happens as \(Q\) approaches \(P\) or, equivalently, as \(x\) approaches \(a\). Figure 3.2 suggests that the secant lines get progressively closer to the tangent line. If we imagine \(Q\) moving toward \(P\), then the secant line appears to rotate into the tangent line as in (D). Therefore, we may expect the slopes of the secant lines to approach the slope of the tangent line.
Based on this intuition, we define the derivative \(f(a)\) (which is read “\(f\) prime of \(a\)”) as the limit
\[f'(a) = \underbrace{\lim\limits_{x\rightarrow a}\frac{f(x) - f(a)}{x-a}}_{\scriptstyle\text{Limit of slopes of secant lines}}\]
121
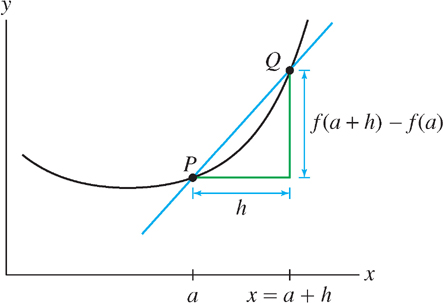
There is another way of writing the difference quotient using a new variable \(h\):
\[h = x - a\]
We have \(x = a + h\) and, for \(x \neq a\) (Figure 3.3),
\[\frac{f(x) - f(a)}{x-a} = \frac{f(a+h) - f(a)}{h}\]
The variable \(h\) approaches 0 as \(x \rightarrow a\), so we can rewrite the derivative as
\[f'(a) = \lim\limits_{h\rightarrow 0}\frac{f(a+h) - f(a)}{h}\]
Each way of writing the derivative is useful. The version using h is often more convenient in computations.
DEFINITION The Derivative
The derivative of \(f(x)\) at \(x = a\) is the limit of the difference quotients (if it exists):
\[f'(a) = \lim\limits_{h\rightarrow 0}\frac{f(a+h) - f(a)}{h}\tag{1}\]
When the limit exists, we say that \(f\) is differentiable at \(x = a\). An equivalent definition of the derivative is
\[f'(a) = \lim\limits_{x\rightarrow a}\frac{f(x) - f(a)}{x-a}\tag{2}\]
We now have the concepts to define precisely what is meant by a curve given by \(y=f(x)\) having a (non-vertical) tangent line at the point \(P(a,f(a))\), namely as the line with slope \(f'(a)\) through \(P\).
DEFINITION Tangent Line
Assume that \(f(x)\) is differentiable at \(x = a\). The tangent line to the graph of \(y = f(x)\) at \(P = (a, f(a))\) is the line through \(P\) of slope \(f'(a)\). The equation of the tangent line in point-slope form is
REMINDER The equation of the line through \(P = (a, b) \) of slope \(m\) in point-slope form:
\(y - b = m(x - a)\)
\[y-f(a) = f'(a) (x-a)\tag{3}\]
122
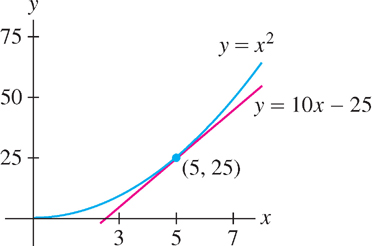
EXAMPLE 1 Equation of a Tangent Line
Find an equation of the tangent line to the graph of \(f(x) = x^2\) at \(x = 5\).
Solution First, we must compute \(f'(5)\). We are free to use either Eq. (1) or Eq. (2). Using Eq. (2), we have
\begin{align*} f'(5) & =\lim\limits_{x\rightarrow 5} \frac{f(x) - f(5)}{x-5} = \lim\limits_{x\rightarrow 5} \frac{x^2 - 25}{x-5} = \lim\limits_{x\rightarrow 5}\frac{(x-5)(x+5)}{x-5}\\[5pt] & =\lim\limits_{x\rightarrow 5} (x+5) = 10 \end{align*}
Next, we apply Eq. (3) with \(a = 5\). Because \(f(5) = 25\), an equation of the tangent line is \(y - 25 = 10(x - 5)\), or, in slope-intercept form: \(y = 10x - 25\) (Figure 3.4).
Isaac Newton referred to calculus as the “method of fluxions” (from the Latin word for “flow”), but the term “differential calculus”, introduced in its Latin form “calculus differentialis” by Gottfried Wilhelm Leibniz, eventually won out and was adopted universally.
The next two examples illustrate differentiation (the process of computing the derivative) using Eq. (1). For clarity, we break up the computations into three steps.
EXAMPLE 2
Compute \(f'(3)\), where \(f(x) = x^{2} - 8x\).
Solution Using Eq. (1), we write the difference quotient at \(a = 3\) as
\[\frac{f(a+h)-f(a)}{h} = \frac{f(3+h)-f(3)}{h} \]
Step 1. Write out the numerator of the difference quotient.
\begin{align*}\frac{f(3+h)-f(3)}{h} & = \left((3+h)^2 - 8(3+h)\right) - \left(3^2 - 8(3)\right)\\ & = \left((9+6h+h^2) - (24+8h)\right) - \left(9-24\right)\\ & = h^2 - 2h\end{align*}
Step 2. Divide by \(h\) and simplify.
\[\frac{f(3+h)-f(3)}{h} = \frac{h^2 - 2h}{h} = \underbrace{\frac{h(h-2)}{h}=h-2}_{\text{Cancel }h}\]
Step 3. Compute the limit.
\[f'(3) = \lim\limits_{h\rightarrow 0}\frac{f(3+h)-f(3)}{h} =\lim\limits_{h\rightarrow 0}h-2 = -2 \]
Question 3.1 Derivative Progress Check 1
xdnzduW6ihz5qzz6PvsbfdQYYWB12WxK4CJNNlOpL0IlX+Wq+h6XLhl2fE640Zn6UOfb9K7AtkKS0KkAPzXs9yIJ/UjJ7NLsiskWLHb4q27oXeg9ii5ttZUetFIbhuk/lJ67fTm5SgXC8+wMta5jNQqQPbZtubR0kMRHsYgFv0V0GzReZwSHaX8AYgaM1ORXWB+kympXYqVyhnu8JoNoLQxP9fD8JQ/iEXAMPLE 3
Sketch the graph of \(f(x)=\dfrac{1}{x}\) and the tangent line at \(x = 2\).
(a) Based on the sketch, do you expect \(f'(2)\) to be positive or negative?
(b) Find an equation of the tangent line at \(x = 2\).
Solution The graph and tangent line at \(x = 2\) are shown in Figure 3.5.
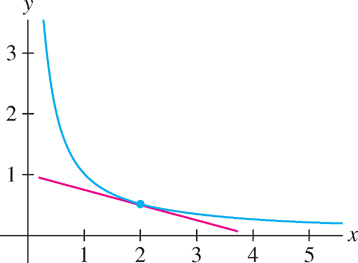
(a) We see that the tangent line has negative slope, so \(f'(2)\) must be negative.
(b) We compute \(f'(2)\) in three steps as before.
Step 1. Write out the numerator of the difference quotient.
\[f(2+h) - f(2) = \frac{1}{2+h} - \frac{1}{2} = \frac{2}{2(2+h)} - \frac{2+h}{2(2+h)} = -\frac{h}{2(2+h)}\]
Step 2. Divide by \(h\) and simplify.
\[\frac{f(2+h) - f(2)}{h} = \frac{1}{h}\cdot\left(-\frac{h}{2(2+h)}\right) = -\frac{1}{2(2+h)}\]
123
Step 3. Compute the limit.
\[f'(2) = \lim\limits_{h\rightarrow 0}\frac{f(2+h) - f(2)}{h} =\lim\limits_{h\rightarrow 0}-\frac{1}{2(2+h)} = -\frac{1}{4}\]
The function value is \(f(2) = \frac{1}{2}\), so the tangent line passes through \(\left(2,\frac{1}{2}\right)\) and has equation
\[y-\frac{1}{2} = -\frac{1}{4}(x-2)\]
In slope-intercept form, \(y=-\frac{1}{4}x+1\).
Question 3.2 Derivatives Progress Check 2
6Cjm/CyOAGmVZJ2ln1h1J71/1ogX4ppuVxu1SfsOthvYlOCNf/lOYc9gWDNtx6Qqlvk4LFz6f6uyO6kLThe graph of a linear function \(f(x) = mx + b\) (where \(m\) and \(b\) are constants) is a line of slope \(m\). The tangent line at any point coincides with the line itself (Figure 3.6), so we should expect that \(f'(a) = m\) for all \(a\). Let’s check this by computing the derivative:
\begin{align*}f'(a) &= \lim\limits_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h} = \lim\limits_{h\rightarrow 0} \frac{(m(a+h)+b)-(ma+b)}{h} \\[5pt] & =\lim\limits_{h\rightarrow 0}\frac{mh}{h} = \lim\limits_{h\rightarrow 0}m = m \end{align*}
If \(m = 0\), then \(f(x) = b\) is constant and \(f'(a) = 0\) (Figure 3.7). In summary,
THEOREM 1 Derivative of Linear and Constant Functions
- If \(f(x) = mx + b\) is a linear function, then \(f'(a) = m\) for all \(a\).
- If \(f(x) = b\) is a constant function, then \(f'(a) = 0\) for all \(a\).
EXAMPLE 4
Find the derivative of \(f(x) = 9x - 5\) at \(x = 2\) and \(x = 5\).
Solution We have \(f'(a) = 9\) for all \(a\). Hence, \(f'(2) = f'(5) = 9\).
Question 3.3 Derivative Progress Check 3
MuvEjcMwCiSP3nQ24XXeTInbIyz2M+nF9XLRsMzaR37YgcNgSBcJSIt6jSbafNQvOpacEVZM+v8jPmzilylpmuPAEWQ=3.1.1 Estimating the Derivative
Approximations to the derivative are useful in situations where we cannot evaluate \(f(a)\) exactly. Since the derivative is the limit of difference quotients, the difference quotient should give a good numerical approximation when \(h\) is sufficiently small:
\[f'(a)\approx\frac{f(a+h)-f(a)}{h}\text{ if }h\text{ is small.}\]
Graphically, this says that for small \(h\), the slope of the secant line is nearly equal to the slope of the tangent line (Figure 3.8).
EXAMPLE 5
Estimate the derivative of \(f(x) = \sin x\) at \(x=\frac{\pi}{6}\).
Solution We calculate the difference quotient for several small values of \(h\):
\[\frac{\sin(\frac{\pi}{6} + h)-\sin\frac{\pi}{6}}{h} = \frac{\sin(\frac{\pi}{6} + h)-0.5}{h}\]
Table 3.1 below suggests that the limit has a decimal expansion beginning \(0.866\). In other words, \(f'(\frac{\pi}{6})\approx0.866\).
124
| \(h > 0\) | \(\frac{\sin(\frac{\pi}{6} + h)-0.5}{h}\) | \(h < 0\) | \(\frac{\sin(\frac{\pi}{6} + h)-0.5}{h}\) |
| 0.01 | 0.863511 | −0.01 | 0.868511 |
| 0.001 | 0.865775 | −0.001 | 0.866275 |
| 0.0001 | 0.8660 00 | −0.0001 | 0.866 050 |
| 0.00001 | 0.8660 229 | −0.00001 | 0.8660 279 |
In the next example, we use graphical reasoning to determine the accuracy of the estimates obtained in Example 5.
EXAMPLE 6 Determining Accuracy Graphically
Let \(f(x) = \sin x\). Show that the approximation \(f'(\frac{\pi}{6})\approx0.8660\) is accurate to four decimal places.
Solution Observe in Figure 3.9 that the position of the secant line relative to the tangent line depends on whether \(h\) is positive or negative. When \(h > 0\), the slope of the secant line is smaller than the slope of the tangent line, but it is larger when \(h < 0\). This tells us that the difference quotients in the second column of Table 3.1 are smaller than \(f'(\frac{\pi}{6})\) and those in the fourth column are greater than \(f'(\frac{\pi}{6})\). From the last line in Table 3.1 we may conclude that
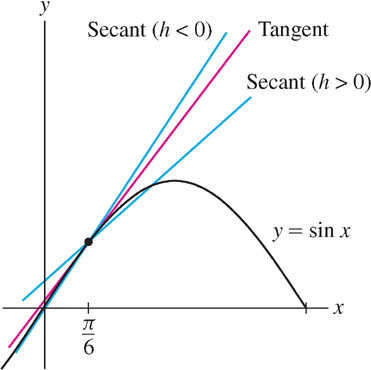
This technique of estimating an unknown quantity by showing that it lies between two known values (“squeezing it”) is used frequently in calculus.
\[0.866022\leq f'(\tfrac{\pi}{6}) \leq 0.866028\]
It follows that the estimate \(f'(\frac{\pi}{6})\approx0.866\) is accurate to four decimal places. In Section 3.6, we will see that the exact value is \(f'(\frac{\pi}{6})=\cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2} \approx0.8660254\), just about midway between 0.866022 and 0.866028.
CONCEPTUAL INSIGHT Are Limits Really Necessary?
It is natural to ask whether limits are really necessary. The tangent line is easy to visualize. Is there perhaps a better or simpler way to find its equation? History gives one answer: The methods of calculus based on limits have stood the test of time and are used more widely today than ever before.
History aside, we can see directly why limits play such a crucial role. The slope of a line can be computed if the coordinates of two points \(P = (x_{1}, y_{1})\) and \(Q = (x_{2}, y_{2})\) on the line are known:
\[\text{Slope of Line} = \frac{y_2-y_1}{x_2 - x_1}\]
This formula cannot be applied to the tangent line because we know only that it passes through the single point \(P = (a, f(a))\). Limits provide an ingenious way around this difficulty. We choose a point \(Q = (a + h, f (a + h))\) on the graph near \(P\) and form the secant line. The slope of this secant line is just an approximation to the slope of the tangent line:
\[\text{Slope of the secant line} = \frac{f(a+h)-f(a)}{h} \approx \text{slope of tangent line}\]
But this approximation improves as \(h \rightarrow 0\), and by taking the limit, we convert our approximations into the exact slope.
125
3.1.2 Section 3.1 Summary
- The difference quotient:
\[\frac{f(a+h)-f(a)}{h}\]
The difference quotient is the slope of the secant line through the points \(P = (a, f(a))\) and \(Q = (a + h, f(a + h))\) on the graph of \(f(x)\).
- The derivative \(f'(a)\) is defined by the following equivalent limits:
\[f'(a) = \lim\limits_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h} = \lim\limits_{x\rightarrow a}\frac{f(x) - f(a)}{x-a}\]
If the limit exists, we say that \(f\) is differentiable at \(x = a\).
- By definition, the tangent line at \(P = (a, f(a))\) is the line through \(P\) with slope \(f'(a)\) [assuming that \(f'(a)\) exists].
- Equation of the tangent line in point-slope form:
\[y - f(a) = f'(a)(x- a)\]
- To calculate \(f'(a)\) using the limit definition:
Step 1. Write out the numerator of the difference quotient.
Step 2. Divide by \(h\) and simplify.
Step 3. Compute the derivative by taking the limit.
- For small values of \(h\), we have the estimate \(f'(a)\approx\frac{f(a+h)-f(a)}{h}\).