3.7 The Chain Rule
The Chain Rule is used to differentiate composite functions such as \(y = \cos(x^{3})\) and \(y=\sqrt{x^4+1}\).
Recall that a composite function is obtained by “plugging” one function into another. The composite of \(f\) and \(g\), denoted \(f\circ g\), is defined by
\[(f\circ g)(x) = f(g(x))\]
For convenience, we call \(f\) the outside function and \(g\) the inside function. Often, we write the composite function as \(f(u)\), where \(u = g(x)\). For example, \(y = \cos(x^{3})\) is the function \(y = \cos u\), where \(u = x^{3}\).
THEOREM 1 Chain Rule
In verbal form, the Chain Rule says
\[(f(g(x))) = \text{outside}'(\text{inside})\cdot\text{inside}'\]
A proof of the Chain Rule is given at the end of this section.
If \(f\) and \(g\) are differentiable, then the composite function \((f\circ g)(x) = f(g(x))\) is differentiable and
\[\boxed{\left(f(g(x))\right)'=f'(g(x)) \cdot g'(x)}\]
CONCEPTUAL INSIGHT
The chain rule is strongly suggested by Leibniz's notation. To see this, set \(u=g(x)\). Then if \(y=f(g(x))=f(u)\), then \(f'(g(x))\), the derivative of \(f\) at the point \(g(x)\) equals \(\displaystyle \frac{dy}{du}\) (evaluated at \(g(x)\) ). By using \(\displaystyle \frac{dy}{du}\) in place of \(f'(g(x))\), we lose some information, namely that the derivative is evaluated at \(g(x)\), but we gain a degree of conceptual simplicity because the equation
\[[f(g(x))]'= f'(g(x)) \cdot g'(x)\]
becomes
\[\frac{dy}{dx}= \frac{dy}{du} \cdot \frac{du}{dx}\]
which (cancelling the \(du\)'s ) is an almost obvious statement.
EXAMPLE 1
Calculate the derivative of \(y = \cos(x^{3})\).
Solution As noted above, \(y = \cos(x^{3})\) is a composite \(f(g(x))\) where
\begin{align*}f(u)&=\cos u &u=g(x)&=x^3 \\ f'(u)&=-\sin u&g'(x)&=3x^2\end{align*}
Note that \(f'(g(x)) = \sin(x^{3})\), so by the Chain Rule,
\[\frac{d}{dx}\cos(x^3)=\underbrace{-\sin(x^3)}_{f'(g(x))}\;\underbrace{(3x^2)}_{g'(x)}=-3x^2\sin(x^3)\]
170
EXAMPLE 2
Calculate the derivative of \(y=\sqrt{x^4 + 1}\).
Solution The function \(y=\sqrt{x^4 + 1}\) is a composite \(f(g(x)\) where
\begin{align*}f(u)&=u^{\frac{1}{2}}&u=g(x)&=x^4 + 1\\[5pt] f'(u)&=\frac{1}{2}u^{-\frac{1}{2}}&g'(x)&=4x^3\end{align*}
Note that \(f'(g(x))=\frac{1}{2}(x^4+1)^{-\frac{1}{2}}\), so by the Chain Rule,
\[\frac{d}{dx}\sqrt{x^4+1}=\underbrace{\frac{1}{2}(x^4+1)^{-\frac{1}{2}}}_{f'(g(x))}\;\underbrace{(4x^3)}_{g'(x)}=\frac{4x^3}{2\sqrt{x^4+1}}\]
Question 3.17 Chain Rule Progress Check 1
5ahPPUx6kmpZpWM9Xl69zRHY+kKrwfogNH0o5MlVV0FyLaO8pvOFNTkDmHOTCMUaRrVDHfvnFAa4sIBXSOglZ8eE1qplX0tjAaTVuyXSWnmfu0LVHWMswCHuJSYM1ENXufekyVwVPSuKyXb0AxNv+6LMTiQKRxFzYUF9t/CBqr972RM9FT04c67Bl3g0WLDzb91ZaH7G87tqirx7f22vkf4cdAwSxz1ib7cRR6SCa5/xg9RJMnbAiNF3QTBeMMJYLbNKcW+qbJMtQgGrq2K4DR9uh5CLKxa1omvBO83qU9escx4/NBIGyQ==EXAMPLE 3
Calculate \(\frac{dy}{dx}\) for \(y=\tan\left(\dfrac{x}{x+1}\right)\).
Solution The outside function is \(f(u) = \tan u\). Because \(f'(u) = \sec^{2}u\), the Chain gives us
\[\frac{d}{dx}\tan\left(\frac{x}{x+1}\right)=\sec^2\left(\frac{x}{x+1}\right)\frac{d}{dx}\left(\frac{x}{x+1}\right)\]
Now, by the Quotient Rule,
\[\frac{d}{dx}\left(\frac{x}{x+1}\right) = \frac{(x+1)\frac{d}{dx}x-x\frac{d}{dx}(x+1)}{(x+1)^2}=\frac{1}{(x+1)^2}\]
We obtain
\[\frac{d}{dx}\tan\left(\frac{x}{x+1}\right) = \sec^2\left(\frac{x}{x+1}\right)\frac{1}{(x+1)^2}=\frac{\sec^2\left(\frac{x}{x+1}\right)}{(x+1)^2}\]
Question 3.18 Chain Rule Progress Check 2
DgmcN/DEASZiwM+EZBnKJ7UPuX43eoCpD2/xtbIYI5h6+FnEirml3ffKeJESudV6mm8Ybv0TwmJB2YiDlbd/g0Bvo/K6vBRHh1w9rgmSyW+eDf5nIhWPY1X8/XqMjruNIy0b8TokP9UuQfkxIt is instructive to write the Chain Rule in Leibniz notation. Let
\(y = f(u) = f(g(x))\)
Then, by the Chain Rule,
\[\frac{dy}{dx}=f'(u)g'(x) = \frac{df}{du}\frac{du}{dx}\]
or
\[\boxed{\dfrac{dy}{dx}=\dfrac{dy}{du}\dfrac{du}{dx}}\]


171
EXAMPLE 4
Imagine a sphere whose radius \(r\) increases at a rate of 3 cm/s. At what rate is the volume \(V\) of the sphere increasing when \(r = 10\text{ cm}\)?
Solution Because we are asked to determine the rate at which \(V\) is increasing, we must find \(\frac{dV}{dt}\). What we are given is the rate \(\frac{dr}{dt}\), namely \(\frac{dr}{dt} = 3\text{ cm/s}\). The Chain Rule allows us to express \(\frac{dV}{dt}\) in terms of \(\frac{dV}{dr}\) and \(\frac{dr}{dt}\):
\[\underbrace{\frac{dV}{dt}}_{\begin{array}{c}\text{Rate of change of volume}\\\text{with respect to time}\end{array}}= \underbrace{\frac{dV}{dr}}_{\begin{array}{c}\text{Rate of change of volume}\\\text{with respect to radius}\end{array}} \times\underbrace{\frac{dr}{dt}}_{\begin{array}{c}\text{Rate of change of radius}\\\text{with respect to time}\end{array}}\]
To compute \(\frac{dV}{dr}\), we use the formula for the volume of a sphere, \(V=\frac{4}{3}\pi r^3\):
\[\frac{dV}{dr}=\frac{d}{dr}\left(\frac{4}{3}\pi r^3\right)=4\pi r^2\]
Because \(\frac{dr}{dt} = 3\), we obtain
\[\frac{dV}{dt}=\frac{dV}{dr}\frac{dr}{dt}=4\pi r^2 3 = 12\pi r^2\]
For \(r = 10\),
\[\frac{dV}{dt}\Bigg|_{r=10}=(12\pi)10^2=1200\pi\approx3770\text{ cm}^3\text{/s}\]
We now discuss some important special cases of the Chain Rule.
THEOREM 2 General Power and Exponential Rules
If \(g(x)\) is differentiable, then
- \(\frac{d}{dx}g(x)^n = n(g(x))^{n-1}g'(x)\) (for any number \(n\))
- \(\frac{d}{dx}e^{g(x)} = g'(x)e^{g(x)}\)
Proof
Let \(f(u) = u^{n}\). Then \(g(x)^{n} = f(g(x))\), and the Chain Rule yields
\[\frac{d}{dx}g(x)^n = f'(g(x))g'(x) = n(g(x))^{n-1}g'(x)\]
172
On the other hand, \(e^{g(x)} = h(g(x))\), where \(h(u) = e^{u}\). We obtain
\[\frac{d}{dx}e^{g(x)}=h'(g(x))g'(x)=e^{g(x)}g'(x) = g'(x)e^{g(x)}\]
EXAMPLE 5 General Power and Exponential Rules
Find the derivatives of (a) \(y = (x^{2} + 7x + 2)^{-1/3}\) and (b) \(y = e^{\cos t}\).
Solution Apply \(\frac{d}{dx}g(x)^n = ng(x)^{n-1}g'(x)\) in (a) and \(\frac{d}{dx}e^{g(x)}=g'(x)e^{g(x)}\) in (b).
(a) \begin{align*}\frac{d}{dx}(x^2+7x+2)&=-\frac{1}{3}(x^2+7x+2)^{-4/3}\frac{d}{dx}(x^2+7x+2)\\[10pt] &=-\frac{1}{3}(x^2+7x+2)^{-4/3}(2x+7)\end{align*}
(b) \[\frac{d}{dt}e^{\cos t}=e^{\cos t}\frac{d}{dt}\cos t=-(\sin t)e^{\cos t}\]
The Chain Rule applied to \(f(kx + b)\) yields another important special case:
\[\frac{d}{dx}f(kx+b) = f'(kx+b)\frac{d}{dx}(kx+b) = kf'(kx+b)\]
THEOREM 3 Shifting and Scaling Rule
If \(f(x)\) is differentiable, then for any constants \(k\) and \(b\),
\[\boxed{\dfrac{d}{dx}f(kx+b)=kf'(kx+b)}\]
For example,
\[\begin{array}{l} \dfrac{d}{dx}\sin\left(2x+\dfrac{\pi}{4}\right)=2\cos\left(2x+\dfrac{\pi}{4}\right)\\[10pt] \dfrac{d}{dx}(9x-2)^5 = (9)(5)(9x-2)^4 = 45(9x-2)^4\\[10pt] \dfrac{d}{dt}\sin(-4t)=-4\cos(-4t)\\[10pt] \dfrac{d}{dt}e^{7-5t}=-5e^{7-5t} \end{array}\]
GRAPHICAL INSIGHT
To understand Theorem 3 graphically, recall that the graphs of \(f(kx + b)\) and \(f(x)\) are related by shifting and scaling (Section 3.6). For example, if \(k > 1\), then the graph of \(f(kx + b)\) is a compressed version of the graph of \(f(x)\) that is steeper by a factor of \(k\). Figure 3.46 illustrates a case with \(k = 2\).
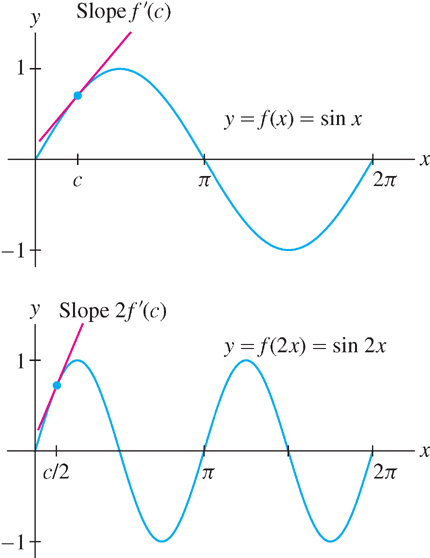
When the inside function is itself a composite function, we apply the Chain Rule more than once, as in the next example.
173
EXAMPLE 6 Using the Chain Rule Twice
Calculate \(\frac{d}{dx}\sqrt{1+\sqrt{x^2+1}}\).
Solution First apply the Chain Rule with inside function \(u=1+\sqrt{x^2+1}\):
\[\frac{d}{dx}\left(1+(x^2+1)^{\frac{1}{2}}\right)^{\frac{1}{2}}=\frac{1}{2}\left(1+(x^2+1)^{\frac{1}{2}}\right)^{-\frac{1}{2}}\frac{d}{dx}\left(1+(x^2+1)^{\frac{1}{2}}\right)\]
Then apply the Chain Rule again to the remaining derivative:
\begin{align*}\frac{d}{dx}\left(1+(x^2+1)^{\frac{1}{2}}\right)^{\frac{1}{2}}&=\frac{1}{2}\left(1+(x^2+1)^{\frac{1}{2}}\right)^{-\frac{1}{2}}\left(\frac{1}{2}(x^2+1)^{-\frac{1}{2}}(2x)\right)\\&=\frac{1}{2}x(x^2+1)^{-\frac{1}{2}}\left(1+(x^2+1)^{\frac{1}{2}}\right)^{-\frac{1}{2}}\end{align*}
Question 3.19 Chain Rule Progress Check 3
/GOq7eIyOJ8ogAAbi9sPto+a5wglQqq1vKmPK+f9OAhhVuGlCFCTeX/EzwZtqj7CLXHXOkBnKtUXOx6tpYSMLzWFDHstAMqFSbr3X/SuxrbjPm6J2olbIg==Proof of the Chain Rule
The difference quotient for the composite \(f\circ g\) is
\[\frac{f(g(x+h))-f(g(x))}{h}\qquad(h\neq0)\]
Our goal is to show that \((f\circ g)'\) is the product of \(f'(g(x))\) and \(g'(x)\), so it makes sense to write the difference quotient as a product:
\[\frac{f(g(x+h))-f(g(x))}{h}=\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}\times\frac{g(x+h)-g(x)}{h}\tag{1}\]
174
This is legitimate only if the denominator \(g(x + h) - g(x)\) is nonzero. Therefore, to continue our proof, we make the extra assumption that \(g(x + h) - g(x)\neq 0\) for all \(h\) near but not equal to 0. This assumption is not necessary, but without it, the argument is more technical (see Exercise 105).
Under our assumption, we may use Eq. (1) to write \((f\circ g)'(x)\) as a product of two limits:
\[(f\circ g)'(x)=\underbrace{\lim\limits_{h\rightarrow 0}\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}}_{\text{Show that this equals }f'(g(x)} \times\underbrace{\lim\limits_{h\rightarrow 0}\frac{g(x+h)-g(x)}{h}}_{\text{This is }g'(x)}\tag{1}\]
The second limit on the right is \(g'(x)\). The Chain Rule will follow if we show that the first limit equals \(f'(g(x))\). To verify this, set \(k = g(x + h) - g(x)\). Then \(g(x + h) = g(x) + k\) and
\[\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}=\frac{f(g(x)+k)-f(g(x))}{k}\]
The function \(g(x)\) is continuous because it is differentiable. Therefore, \(g(x + h)\) tends to \(g(x)\) and \(k = g(x + h) - g(x)\) tends to zero as \(h\rightarrow 0\). Thus, we may rewrite the limit in terms of \(k\) to obtain the desired result:
\[\lim\limits_{h\rightarrow 0}\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}=\lim\limits_{k\rightarrow 0}\frac{f(g(x)+k)-f(g(x))}{k}=f'(g(x))\]
3.7.1 Section 3.7 Summary
- The Chain Rule expresses \((f \circ g)'\) in terms of \(f'\) and \(g'\):
\[(f(g(x)))' = f'(g(x))g'(x)\]
- In Leibniz notation: \(\dfrac{dy}{dx}=\dfrac{dy}{du}\dfrac{du}{dx}\), where \(y = f(u)\) and \(u = g(x)\)
- General Power Rule: \(\dfrac{d}{dx}g(x)^n = ng(x)^{n-1}g'(x)\)
- General Exponential Rule: \(\dfrac{d}{dx}e^{g(x)} = g'(x)e^{g(x)}\)
- Shifting and Scaling Rule: \(\dfrac{d}{dx}f(kx+b) = kf'(kx+b)\)
175