exercises
Question 5.1
Evaluate the following iterated integrals:
- (a) \(\displaystyle\int_{0}^{1} \int_{0}^{1} ( 1 - x^3 + xy ) \, {\it dx}\, {\it dy}\)
- (b) \(\displaystyle\int_{0}^{\pi/2} \int_{-\pi/2}^{\pi/2} \cos x \sin y \, {\it dx}\, {\it dy}\)
- (c) \(\displaystyle\int_{1}^{2} \int_{2}^{4} \left( \frac{x}{y} + \frac{y}{x} \right) \, {\it dx}\, {\it dy}\)
- (d) \(\displaystyle\int_{0}^{\pi/4} \int_{0}^{\pi/4} \tan x \sec^{2} y \, {\it dx}\, {\it dy}\)
270
Question 5.2
Evaluate the integrals in Exercise 1 by integrating first with respect to \(y\) and then with respect to \(x\).
Question 5.3
Evaluate the following iterated integrals:
- (a) \(\displaystyle\int_{-1}^1\int_0^1(x^4y+y^2)\, {\it dy}\,{\it dx}\)
- (b) \(\displaystyle\int_0^{\pi/2}\int_0^1(\,y\cos x+2)\, {\it dy}\,{\it dx}\)
- (c) \(\displaystyle\int_0^1\int_0^1(xye^{x+y})\, {\it dy}\,{\it dx}\)
- (d) \(\displaystyle\int_{-1}^0\int_1^2(-x\log y)\, {\it dy}\,{\it dx}\)
Question 5.4
Evaluate the integrals in Exercise 3 by integrating with respect to \(x\) and then with respect to \(y\). [The solution to part (b) only is in the Study Guide to this text.]
Question 5.5
Use Cavalieri’s principle to show that the volumes of two cylinders with the same base and height are equal (see Figure 5.10).
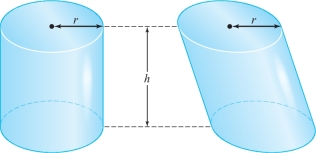
Question 5.6
Using Cavalieri’s principle, compute the volume of the structure shown in Figure 5.11; each cross section is a rectangle of length 5 and width 3.
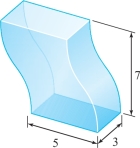
Question 5.7
A lumberjack cuts out a wedge-shaped piece \(W\) of a cylindrical tree of radius \(r\) obtained by making two saw cuts to the tree’s center, one horizontally and one at an angle \(\theta\). Compute the volume of the wedge \(W\) using Cavalieri’s principle. (See Figure 5.12.)
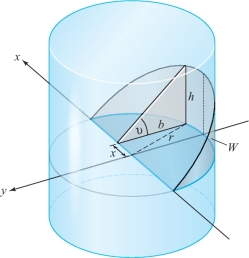
Question 5.8
- (a) Show that the volume of the solid of revolution shown in Figure 5.13 is \[ \pi \int_a^b \, [f(x)]^2\, {\it dx} . \]
- (b) Show that the volume of the region obtained by rotating the region under the graph of the parabola \(y= -x^2+2x+3\), \(-1\leq x\leq 3\), about the \(x\) axis is \(512\pi/15\) [see Figure 5.13].
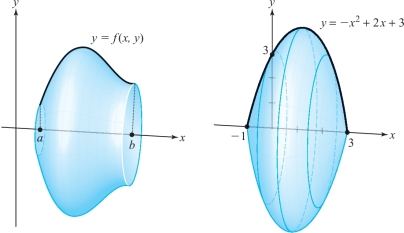
271
Evaluate the double integrals in Exercises 9 to 11, where R is the rectangle \([0,2]\times [-1,0]\).
Question 5.9
\(\displaystyle \intop\!\!\!\intop\nolimits_{R}\, (x^2y^2+x)\, {\it dy}\,{\it dx}\)
Question 5.10
\(\displaystyle \intop\!\!\!\intop\nolimits_{R} \left(|y|\cos\frac{1}{4}\pi x\right) {\it dy}\,{\it dx}\)
Question 5.11
\(\displaystyle \intop\!\!\!\intop\nolimits_{R} \left({-}xe^x\sin\frac{1}{2}\pi y\right) {\it dy}\,{\it dx}\)
Question 5.12
Evaluate the iterated integral: \[ \int_{1}^{3} \int_{1}^{2} \frac{xy}{\left( x^2 + y^2 \right)^{3/2}} \, {\it dx}\, {\it dy}. \]
Question 5.13
Evaluate the iterated integral: \[ \int_{0}^{1} \int_{0}^{1} \left( 3x + 2y \right)^{7} \, {\it dx}\, {\it dy}. \]
Question 5.14
Find the volume bounded by the graph of \(f(x,y)=1+2x+3y\), the rectangle \([1,2]\times [0,1]\), and the four vertical sides of the rectangle \(R\), as in Figure 5.1.
Question 5.15
Repeat Exercise 14 for the function \(f(x,y) = x^4 + y^2\) and the rectangle \([-1,1]\times [-3,-2]\).