Question 5.34

In parts (a) through (d) below, each iterated integral is an integral over a region \(D\). Match the integral with the correct region of integration.

• (a) \(\displaystyle\int_{1}^{2} \int_{\ln x}^{e^x} \, {\it dy}\, {\it dx}\)
• (b) \(\displaystyle\int_{0}^{2} \int_{(1/8) x}^{x^{1/3}} \, {\it dy}\, {\it dx}\)
• (c) \(\displaystyle\int_{0}^{2} \int_{-\sqrt{9 - y^2}}^{0} \, {\it dx}\, {\it dy}\)
• (d) \(\displaystyle\int_{0}^{3} \int_{\arccos y/3}^{0} \, {\it dx}\, {\it dy}\)

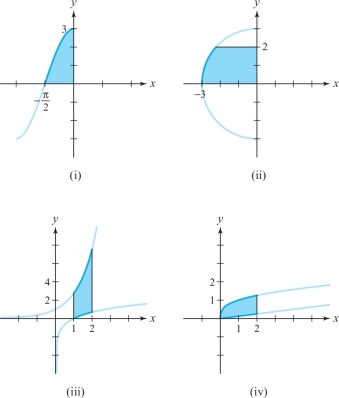
Question 5.35

Sketch the region \(D\) in \(\mathbb R^2\) that represents the region of integration:

• (a) \(\displaystyle\int_{-2}^{2} \int_{0}^{4 - y^2} (4 - x) \, {\it dx}\, {\it dy}\)
• (b) \(\displaystyle\int_{0}^{3} \int_{-x}^{x} (6 + y - 2x) \, {\it dy}\, {\it dx}\)

Question 5.36

Evaluate the following iterated integrals and draw the regions \(D\) determined by the limits. State whether the regions are \(x\)-simple, \(y\)-simple, or simple.

• (a) \(\displaystyle\int_0^1\int_0^{x^{2}} {\it dy}\, {\it dx} \)
• (b) \(\displaystyle\int_1^2\int_{2x}^{3x+1} {\it dy}\,{\it dx} \)
• (c) \(\displaystyle\int_0^1\int_1^{e^x} (x+y)\, {\it dy}\, {\it dx}\)
• (d) \(\displaystyle\int_0^1\int_{x^3}^{x^{2}} y\, {\it dy}\,{\it dx}\)

Question 5.37

Evaluate the following integrals and sketch the corresponding regions.

• (a) \(\displaystyle\int_{-3}^2\int_0^{y^2}(x^2+y)\, {\it dx}\, {\it dy} \)
• (b) \(\displaystyle\int_{-1}^1\int_{-2|x|}^{|x|}e^{x+y} {\it dy}\,{\it dx} \)
• (c) \(\displaystyle\int_0^1 \int_{0}^{(1-x^{2})^{1/2}} {\it dy}\,{\it dx} \)
• (d) \(\displaystyle\int_{0}^{\pi/2}\int_0^{\cos x} y \sin x {\it dy}\,{\it dx} \)
• (e) \(\displaystyle\int_{0}^1\!\int_{y^2}^y\, (x^n\,{+}\,y^m)\, {\it dx}\, {\it dy} , m,n\,{>}\,0\)
• (f) \(\displaystyle\int_{-1}^0\int_{0}^{2(1-x^{2})^{1/2}} x {\it dy}\, {\it dx}\)

289

Question 5.38

Use double integrals to compute the area of a circle of radius \(r\).

Question 5.39

Using double integrals, determine the area of an ellipse with semiaxes of length \(a\) and \(b\).

Question 5.40

What is the volume of a barn that has a rectangular base 20 ft by 40 ft, vertical walls 30 ft high at the front (which we assume is on the 20-ft side of the barn), and 40 ft high at the rear? The barn has a flat roof. Use double integrals to compute the volume.

Question 5.41

Let \(D\) be the region bounded by the positive \(x\) and \(y\) axes and the line \(3x + 4y = 10\). Compute \[ \intop\!\!\!\intop\nolimits_{D}\, (x^2+y^2) \,{\it dA}. \]

Question 5.42

Let \(D\) be the region bounded by the \(y\) axis and the parabola \(x=-4y^2+3\). Compute \[ \intop\!\!\!\intop\nolimits_{D}\, x^3 y\, {\it dx}\, {\it dy} . \]

Question 5.43

Evaluate \(\displaystyle\int_0^1\int_0^{x^2}(x^2+xy-y^2)\, {\it dy}\, {\it dx}\). Describe this iterated integral as an integral over a certain region \(D\) in the \(xy\) plane.

Question 5.44

Let \(D\) be the region given as the set of \((x,y)\), where \(1\leq x^2+y^2\leq 2\) and \(y\geq 0\). Is \(D\) an elementary region? Evaluate \({\intop\!\!\!\intop}_Df(x,y)\ {\it dA}\), where \(f(x,y)=1+xy\).

Question 5.45

Evaluate the following double integral: \[ \intop\!\!\!\intop\nolimits_{D} \cos y \, {\it dx}\, {\it dy}, \] where the region \(D\) is bounded by \(y=2x\), \(y=x\), \(x=\pi\), and \(x=2 \pi\).

Question 5.46

Evaluate the following double integral: \[ \intop\!\!\!\intop\nolimits_{D} xy \, {\it dA}, \] where the region \(D\) is the triangular region whose vertices are \((0,0), (0,2), (2,0)\).

Question 5.47

Use the formula \(A(D)= {\intop\!\!\!\intop}_D \, {\it dx}\, {\it dy}\) to find the area enclosed by one period of the sine function \(\sin x\), for \(0\leq x\leq 2\pi\), and the \(x\) axis.

Question 5.48

Find the volume of the region inside the surface \(z=x^2+y^2\) and between \(z=0\) and \(z=10\).

Question 5.49

Set up the integral required to calculate the volume of a cone of base radius \(r\) and height \(h\).

Question 5.50

Evaluate \({\intop\!\!\!\intop}_D y\ {\it dA}\), where \(D\) is the set of points \((x,y)\) such that \(0\leq 2x/\pi\leq y, y\leq \sin x\).

Question 5.51

From Exercise 9, Section 5.3, \(\displaystyle\int_a^b\int_c^d f(x)g(y)\, {\it dy}\, {\it dx} = \left(\int_a^b f(x)\, {\it dx}\right)\!\) \(\displaystyle\left(\int_c^d g(y)\, {\it dy} \right)\). Is it true that \(\intop\!\!\!\intop\nolimits_D f(x) g(y)\ {\it dx} \ {\it dy} =\displaystyle\left(\int^b_a f(x)\ {\it dx} \right) \!\left(\int^{\phi_2(b)}_{\phi_1(a)}g(y)\ {\it dy}\right)\) for \(y\)-simple regions?

Question 5.52

Let \(D\) be a region given as the set of \((x, y)\) with \(-\phi(x)\leq y\leq \phi(x)\) and \(a\leq x\leq b\), where \(\phi\) is a nonnegative continuous function on the interval \([a,b]\). Let \(f(x,y)\) be a function on \(D\) such that \(f(x,y)=-f(x,-y)\) for all \((x,y)\in D\). Argue that \({\intop\!\!\!\intop}_D f(x,y)\, {\it dA}=0\).

Question 5.53

Use the methods of this section to show that the area of the parallelogram \(D\) determined by two planar vectors \({\bf a}\) and \({\bf b}\) is \(|a_1b_2-a_2b_1|\), where \({\bf a}=a_1 {\bf i}+a_2 {\bf j}\) and \({\bf b} =b_1{\bf i}+b_2 {\bf j}\).

Question 5.54

Describe the area \(A(D)\) of a region as a limit of areas of inscribed rectangles, as in Example 3.