Question 8.148

Let \({\bf F} = 2yz{\bf i} + (-x + 3y + 2){\bf j} + (x^2 + z){\bf k}\). Evaluate \({\intop\!\!\!\intop}_S\,({\nabla}\times {\bf F}) {\,{{\cdot}}\,} {\,d} {\bf S}\), where \(S\) is the cylinder \(x^2 + y^2 = a^2\), \(0 \le z \le 1\) (without the top and bottom). What if the top and bottom are included?

Question 8.149

Let \({W}\) be a region in \({\mathbb R}^3\) with boundary \(\partial\!{W}\). Prove the identity \begin{eqnarray*} &&\intop\!\!\!\intop\nolimits_{\!{\partial\! {W}}} [{\bf F}\times ({\nabla} \times {\bf G})] \,{\cdot}\, {\,d} S = \intop\!\!\!\intop\!\!\!\intop\nolimits_{{W}} ({\nabla} \times {\bf F}) \,{\cdot}\, ({\nabla} \times {\bf G}) {\,d} V \\ &&\quad {-}\,\intop\!\!\!\intop\!\!\!\intop\nolimits_{\! {W}} {\bf F} {\,{\cdot}\,} ({\nabla}\times {\nabla} \times {\bf G}){\,d} V.\\[-13pt] \end{eqnarray*}

Question 8.150

Let \({\bf F} = x^2 y{\bf i} +z^8{\bf j} - 2xyz{\bf k}\). Evaluate the integral of \({\bf F}\) over the surface of the unit cube.

Question 8.151

Verify Green’s theorem for the line integral \[ \int_C x^2 y\, {\it {\,d} x} + y\, {\it dy}, \] when \(C\) is the boundary of the region between the curves \(y = x\) and \(y = x^3,\ 0 \le x \le 1\).

Question 8.152

• (a) Show that \({\bf F} = (x^3 - 2xy^3){\bf i} - 3x^2 y^2 {\bf j}\) is a gradient vector field.
• (b) Evaluate the integral of \({\bf F}\) along the path \(x = \cos^3 \theta, y=\sin^3\theta, 0 \le \theta \le \pi/2\).

Question 8.153

Can you derive Green’s theorem in the plane from Gauss’ theorem?

Question 8.154

• (a) Show that \({\bf F} = 6xy(\cos z){\bf i} +3x^2(\cos z){\bf j}- 3x^2y(\sin z){\bf k}\) is conservative (see Section 8.4).
• (b) Find \(f\) such that \({\bf F} = {\nabla}f\).
• (c) Evaluate the integral of \({\bf F}\) along the curve \(x=\cos^3\theta\), \(y = \sin^3\theta\), \(z=0\), \(0\le \theta \le \pi/2\).

Question 8.155

Let \({\bf r}(x,y,z) = (x,y,z), r = \|{\bf r}\|\). Show that \({\nabla}^2 (\log r) = 1/r^2\) and \({\nabla}^2(r^n) = n(n+1)r^{n-2}\).

Question 8.156

Let the velocity of a fluid be described by \({\bf F} = 6xz{\bf i}+ x^2y{\bf j} + yz{\bf k}\). Compute the rate at which fluid is leaving the unit cube.

Question 8.157

Let \({\bf F} = x^2{\bf i} + (x^2 y - 2xy){\bf j} - x^2z{\bf k}\). Does there exist a \({\bf G}\) such that \({\bf F}= {\nabla} \times {\bf G}\)?

Question 8.158

Let \({\bf a}\) be a constant vector and \({\bf F} = {\bf a} \times {\bf r}\) [as usual, \({\bf r}(x,y,z)= (x,y,z)\)]. Is \({\bf F}\) conservative? If so, find a potential for it.

Question 8.159

Show that the fields \({\bf F}\) in (a) and (b) are conservative and find a function \(f\) such that \({\bf F} = {\bf V}f\).

• (a) \({\bf F} = \big(y^2e^{xy^2}\big){\bf i} + \big(2y\,e^{xy^2}\big){\bf j}\)
• (b) \({\bf F} = (\sin y){\bf i} + (x \cos y){\bf i} + (e^z){\bf k}\)

Question 8.160

• (a) Let \(f(x,y,z)= 3xye^{z^2}\). Compute \({\nabla}f\).
• (b) Let \({\bf c}(t) = (3\cos^3 t, \sin^2 t, e^t)\), \(0\le t \le \pi\). Evaluate \[ \int_{\bf c}{\nabla} f \,{\cdot}\, {\,d} {\bf s}. \]
• (c) Verify directly Stokes’ theorem for gradient vector fields \({\bf F} = {\nabla} f\).

491

Question 8.161

Using Green’s theorem, or otherwise, evaluate \(\int_C x^3 {\it dy} - y^3{\it {\,d} x}\), where \(C\) is the unit circle \((x^2 + y^2=1)\).

Question 8.162

Evaluate the integral \({\intop\!\!\!\intop}_S{\bf F}{\,{\cdot}\,} {\,d} {\bf S}\), where \({\bf F} = x{\bf i} + y{\bf j} + 3{\bf k}\) and where \(S\) is the surface of the unit sphere \(x^2 + y^2 + z^2 =1\).

Question 8.163

• (a) State Stokes’ theorem for surfaces in \({\mathbb R}^3\).
• (b) Let \({\bf F}\) be a vector field on \({\mathbb R}^3\) satisfying \({\nabla}\times {\bf F} = {\bf 0}\). Use Stokes’ theorem to show that \(\int_C {\bf F}\,{\cdot}\,{\,d} {\bf s}=0\) where \(C\) is a closed curve.

Question 8.164

Use Green’s theorem to find the area of the loop of the curve \(x = a\sin\theta\cos\theta, y = a \sin^2\theta\), for \(a > 0\) and \(0 \le \theta \le \pi\).

Question 8.165

Evaluate \(\int_Cy z\, {\it {\,d} x} + x z\, {\it dy} +xy{\,d} z\), where \(C\) is the curve of intersection of the cylinder \(x^2 + y^2 = 1\) and the surface \(z = y^2\).

Question 8.166

Evaluate \(\int_C(x+y)\,{\it {\,d} x} + (2x - z)\,{\it dy} + (y+z){\,d} z\), where \(C\) is the perimeter of the triangle connecting \((2,0,0),(0,3,0)\), and \((0,0,6)\), in that order.

Question 8.167

Which of the following are conservative fields on \({\mathbb R}^3\)? For those that are, find a function \(f\) such that \({\bf F}={\nabla}f\).

• (a) \({\bf F}(x,y,z) = 3x^2y{\bf i} + x^3 {\bf j} + 5{\bf k}\)
• (b) \({\bf F}(x,y,z) = (x+z){\bf i} - (y+z){\bf j} + (x-y){\bf k}\)
• (c) \({\bf F}(x,y,z) = 2xy^3{\bf i} + x^2 z^3{\bf j} + 3x^2yz^2{\bf k}\)

Question 8.168

Consider the following two vector fields in \({\mathbb R}^3\):

• (i) \({\bf F}(x,y,z) = y^2 {\bf i} - z^2{\bf j} + x^2 {\bf k}\)
• (ii)\({\bf G}(x,y,z) = (x^3 - 3xy^2){\bf i} + (y^3 - 3x^2 y){\bf j} + z{\bf k}\)

• (a) Which of these fields (if any) are conservative on \({\mathbb R}^3\)? (That is, which are gradient fields?) Give reasons for your answer.
• (b) Find potential for the fields that are conservative.
• (c) Let \({\alpha}\) be the path that goes from \((0,0,0)\) to \((1,1,1)\) by following edges of the cube \(0\le x \le 1\), \(0\le y \le 1\), \(0\le z \le 1\) from \((0,0,0)\) to \((0,0,1)\) to \((0,1,1)\) to \((1,1,1)\). Let \({\beta}\) be the path from \((0,0,0)\) to \((1,1,1)\) directly along the diagonal of the cube. Find the values of the line integrals \[ \int_{\tiny\alpha} {\bf F}\,{\cdot}\, {\,d} {\bf s}, \qquad \int_{\tiny\alpha} {\bf G}\,{\cdot}\, {\,d} {\bf s},\qquad \int_{\tiny\beta}{\bf F}\,{\cdot}\, {\,d} {\bf s}, \qquad \int_{\tiny\beta} {\bf G}\,{\cdot}\, {\,d} {\bf s}. \]

Question 8.169

Consider the constant vector field \({\bf F}(x,y,z) = {\bf i} + 2{\bf j} - {\bf k}\) in \({\mathbb R}^3\).

• (a) Find a scalar field \(\phi(x,y,z)\) in \({\mathbb R}^3\) such that \({\nabla}\phi = {\bf F}\) in \({\mathbb R}^3\) and \(\phi(0,0,0)=0\).
• (b) On the sphere \(\Sigma\) of radius 2 about the origin, find all the points at which
  • (i) \(\phi\) is a maximum, and
  • (ii) \(\phi\) is a minimum.
• (c) Compute the maximum and minimum values of \(\phi\) on \(\Sigma\).

Question 8.170

Let \({\bf F}\) be a \(C^1\) vector field and suppose \({\nabla}{\,{\cdot}\,} {\bf F}(x_0,y_0,z_0) > 0\). Show that for a sufficiently small sphere \(S\) centered at \((x_0,y_0,z_0)\), the flux of \({\bf F}\) out of \(S\) is positive.

Question 8.171

Let \(B \subset {\mathbb R}^{3}\) be a planar region, and let O \(\in {\mathbb R}^{3}\) be a point. If we connect all points in \(B\) to O, we get a cone, say \(C\), with vertex O and base \(B\). Show that \[ \hbox{Volume } (C) = \frac{1}{3} \hbox{ area } (B) \ h, \] where \(h\) is the distance of O from the plane of \(B\), using the following steps.

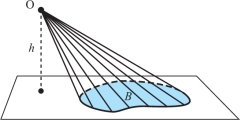
1. Let O be the origin of the coordinate system. Define \({\bf r}(x, y, z)\!\!:\ = (x, y, z)\). Evaluate the flux of \({\bf r}\) through the boundary of \(C\), that is, \({\intop\!\!\!\intop}_{\partial C} {\bf r} \, {\cdot}\, {\bf n}\, {\it dA}\), where \({\bf n}\) is the outward unit normal to \(\partial C\).
2. Evaluate the total divergence \({\intop\!\!\!\intop\!\!\!\intop}_{C} \nabla \, {\cdot}\, {\bf r}\, {\it dV}\).
3. Use Gauss’ theorem, which states that the total divergence of a vector field within a region enclosed by a surface is equal to the flux of that vector field through the surface: \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{C} \nabla \, {\cdot}\, {\bf r}\, {\it dV} = \intop\!\!\!\intop\nolimits_{\partial C} {\bf r} \, {\cdot}\, {\bf n} \,{\it dA.} \]