Question 17.87

What is the flux of \({\bf F}=\langle 1,0,0\rangle\) through a closed surface?

Question 17.88

Justify the following statement: The flux of \({\bf F}=\langle x^3,y^3,z^3\rangle\) through every closed surface is positive.

Question 17.89

Which of the following expressions are meaningful (where \({\bf F}\) is a vector field and \(f\) is a function)? Of those that are meaningful, which are automatically zero?

• (a) \(\hbox{div}(\nabla f)\)
• (b) \({\bf curl}(\nabla f)\)
• (c) \(\nabla{\bf curl}(f)\)
• (d) \(\hbox{div}({\bf curl}({\bf F}))\)
• (e) \({\bf curl}(\hbox{div}({\bf F}))\)
• (f) \(\nabla(\hbox{div}({\bf F}))\)

Question 17.90

Which of the following statements is correct (where \({\bf F}\) is a continuously differentiable vector field defined everywhere)?

• (a) The flux of \({\bf curl}({\bf F})\) through all surfaces is zero.
• (b) If \({\bf F} = \nabla\varphi\), then the flux of \({\bf F}\) through all surfaces is zero.
• (C) The flux of \({\bf curl}({\bf F})\) through all closed surfaces is zero.

Question 17.91

How does the Divergence Theorem imply that the flux of \({\bf F} = \langle x^2, y-e^z, y-2zx\rangle\) through a closed surface is equal to the enclosed volume?

Question 17.92

\(\displaystyle{{\bf F} = \langle xy,yz,y^2-x^3\rangle}\)

Question 17.93

\(\displaystyle{x{\bf i}+y{\bf j}+z{\bf k}}\)

Question 17.94

\(\displaystyle{{\bf F} = \langle x-2zx^2,z-xy,z^2x^2\rangle}\)

Question 17.95

\(\displaystyle{\sin(x+z){\bf i}-ye^{xz}{\bf k}}\)

Question 17.96

Find a constant \(c\) for which the velocity field \[ {\bf v} = (cx - y){\bf i} + (y - z){\bf j} + (3x + 4cz){\bf k} \] of a fluid is incompressible [meaning that \(\hbox{div}({\bf v})=0\)].

Question 17.97

Verify that for any vector field \({\bf F} = \langle F_1, F_2, F_3\rangle\), \[ \hbox{div}({\bf curl}({\bf F}))=0 \]

Question 17.98

\({\bf F} = \langle z,x,y\rangle\), the box \([0,4]\times[0,2]\times[0,3]\)

Question 17.99

\({\bf F} = \langle y,x,z\rangle\), the region \(x^2+y^2+z^2\le 4\)

Question 17.100

\({\bf F} = \langle 2x,3z,3y\rangle\), the region \(x^2+y^2\le 1\), \(0\le z \le 2\)

Question 17.101

\({\bf F} = \langle x,0,0\rangle\), the region \(x^2+y^2\le z \le 4\)

Question 17.102

\({\bf F} = \langle 0,0,z^3/3 \rangle\), \(S\) is the sphere \(x^2+y^2+z^2=1\).

Question 17.103

\({\bf F} = \langle y, z, x \rangle\), \(S\) is the sphere \(x^2+y^2+z^2=1\).

Question 17.104

\({\bf F} = \langle x^3,0,z^3\rangle\), \(S\) is the octant of the sphere \(x^2+y^2+z^2=4\), in the first octant \(x\ge 0, y\ge 0, z\ge 0\).

Question 17.105

\({\bf F} = \langle e^{x+y}, e^{x+z}, e^{x+y} \rangle\), \(S\) is the boundary of the unit cube \(0\le x \le 1, 0 \le y \le 1, 0 \le z\le 1\).

Question 17.106

\({\bf F} = \langle x,y^2,z+y \rangle\), \(S\) is the boundary of the region contained in the cylinder \(x^2+y^2= 4\) between the planes \(z=x\) and \(z=8\).

Question 17.107

\({\bf F} = \langle x^2-z^2, e^{z^2}-\cos x, y^3 \rangle\), \(S\) is the boundary of the region bounded by \(x+2y+4z=12\) and the coordinate planes in the first octant.

Question 17.108

\({\bf F} = \langle x+y, z, z-x\rangle\), \(S\) is the boundary of the region between the paraboloid \(z=9-x^2-y^2\) and the \(xy\)-plane.

Question 17.109

\({\bf F} = \langle e^{z^2}, 2y+\sin(x^2z), 4z+\sqrt{x^2+9y^2} \rangle\), \(S\) is the region\newline \) x^2+y^2\le z \le 8-x^2-y^2\).

Question 17.110

Calculate the flux of the vector field \({\bf F} = 2xy{\bf i}- y^2{\bf j}+{\bf k}\) through the surface \(S\) in Figure 17.70. Hint: Apply the Divergence Theorem to the closed surface consisting of \(S\) and the unit disk.

Question 17.111

Let \(S_1\) be the closed surface consisting of \(S\) in Figure 17.70 together with the unit disk. Find the volume enclosed by \(S_1\), assuming that \[ \iint_{S_1}\langle x, 2y, 3z \rangle\cdot\,d{\bf S} = 72 \]

Figure 17.70: Surface \(S\) whose boundary is the unit circle.

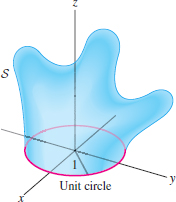
Question 17.112

Let \(S\) be the half-cylinder \(x^2+y^2=1\), \(x\ge 0\), \(0\le z\le 1\). Assume that \({\bf F}\) is a horizontal vector field (the \(z\)-component is zero) such that \({\bf F}(0,y,z) = zy^2{\bf i}\). Let \(W\) be the solid region enclosed by \(S\), and assume that \[ \iiint_{W\,} \hbox{div}({\bf F})\, dV = 4 \] Find the flux of \({\bf F}\) through the curved side of \(S\).

Question 17.113

Volume as a Surface Integral Let \({\bf F} = \langle x, y, z\rangle\). Prove that if \(W\) is a region \({\bf R}^3\) with a smooth boundary \(S\), then \begin{equation} \textrm{Volume}(W) = \frac13\iint_{S\,}{\bf F}\cdot d{\bf S}\tag{10} \end{equation}

Question 17.114

Use Eq. (10) to calculate the volume of the unit ball as a surface integral over the unit sphere.

Question 17.115

Verify that Eq. (10) applied to the box \([0,a]\times[0,b]\times[0,c]\) yields the volume \(V=abc\).

Question 17.116

Let \(W\) be the region in Figure 17.71 bounded by the cylinder \(x^2+y^2=4\), the plane \(z=x+1\), and the \(xy\)-plane. Use the Divergence Theorem to compute the flux of \({\bf F}=\langle z, x, y + z^2\rangle\) through the boundary of \(W\).

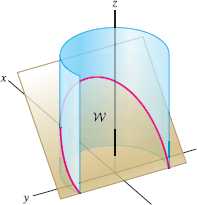
Question 17.117

Let \(\displaystyle{I=\iint_{S\,} {\bf F}\cdot d{\bf S}}\), where \[ {\bf F} = \langle \frac{2yz}{r^2},-\frac{xz}{r^2},-\frac{xy}{r^2}\rangle \] (\(r=\sqrt{x^2+y^2+z^2}\)) and \(S\) is the boundary of a region \(W\).

• (a) Check that \({\bf F}\) is divergence-free.
• (b) Show that \(I=0\) if \(S\) is a sphere centered at the origin. Explain, however, why the Divergence Theorem cannot be used to prove this.

Question 17.118

The velocity field of a fluid \({\bf v}\) (in meters per second) has divergence \(\hbox{div}({\bf v})(P)=3\) at the point \(P=(2,2,2)\). Estimate the flow rate out of the sphere of radius \(0.5\) centered at \(P\).

Question 17.119

A hose feeds into a small screen box of volume \(10\) cm\(^3\) that is suspended in a swimming pool. Water flows across the surface of the box at a rate of \(12\) cm\(^3\)/s. Estimate \(\hbox{div}({\bf v})(P)\), where \({\bf v}\) is the velocity field of the water in the pool and \(P\) is the center of the box. What are the units of \(\hbox{div}({\bf v})(P)\)?

Question 17.120

The electric field due to a unit electric dipole oriented in the \({\bf k}\)-direction is \(\displaystyle{{\bf E}= \nabla ({z}/{r^3} )}\), where \(r=(x^2+y^2+z^2)^{1/2}\) (Figure 17.72). Let \(\displaystyle{{\bf e}_r =r^{-1}\langle x, y, z\rangle}\).

• (a) Show that \(\displaystyle{{\bf E} = r^{-3}{\bf k}-3zr^{-4}{\bf e}_r }\).
• (b) Calculate the flux of \({\bf E}\) through a sphere centered at the origin.
• (c) Calculate \(\hbox{div}({\bf E})\).
• (d) Can we use the Divergence Theorem to compute the flux of \({\bf E}\) through a sphere centered at the origin?

Figure 17.72: The dipole vector field restricted to the \(xz\)-plane.

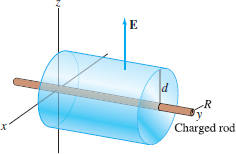
Question 17.121

Let \({\bf E}\) be the electric field due to a long, uniformly charged rod of radius \(R\) with charge density \(\delta\) per unit length (Figure 17.73). By symmetry, we may assume that \({\bf E}\) is everywhere perpendicular to the rod and its magnitude \(E(d)\) depends only on the distance \(d\) to the rod (strictly speaking, this would hold only if the rod were infinite, but it is nearly true if the rod is long enough). Show that \(\displaystyle{E(d) = {\delta}/{2\pi\epsilon_0 d}}\) for \(d>R\). Hint: Apply Gauss’s Law to a cylinder of radius \(R\) and of unit length with its axis along the rod.

Question 17.122

Let \(W\) be the region between the sphere of radius \(4\) and the cube of side \(1\), both centered at the origin. What is the flux through the boundary \(S=\partial W\) of a vector field \({\bf F}\) whose divergence has the constant value \(\hbox{div}({\bf F})=-4\)?

Question 17.123

Let \(W\) be the region between the sphere of radius \(3\) and the sphere of radius \(2\), both centered at the origin. Use the Divergence Theorem to calculate the flux of \({\bf F} = x {\bf i}\) through the boundary \(S=\partial W\).

Question 17.124

Find and prove a Product Rule expressing \(\hbox{div}(f{\bf F})\) in terms of \(\hbox{div}({\bf F})\) and \(\nabla f\).

Question 17.125

Prove the identity \[ \hbox{div}({\bf F}\times{\bf G}) = {\bf curl}({\bf F}) \cdot {\bf G} - {\bf F} \cdot {\bf curl}({\bf G}) \] Then prove that the cross product of two irrotational vector fields is incompressible [\({\bf F}\) is called irrotational if \({\bf curl}({\bf F})=0\) and incompressible if \(\hbox{div}({\bf F})=0\)].

Question 17.126

Prove that \(\hbox{div}(\nabla f\times\nabla g)=0\).

Question 17.127

Prove the identity \[ {\bf curl}({\bf curl}({\bf F}))=\nabla(\hbox{div}({\bf F}))-\Delta{\bf F} \] where \(\Delta {\bf F}\) denotes \(\langle \Delta F_1,\Delta F_2,\Delta F_3\rangle\).

Question 17.128

A function \(\varphi\) satisfying \(\Delta\varphi=0\) is called harmonic.

• (a) Show that \(\Delta\varphi = \hbox{div}(\nabla \varphi)\) for any function \(\varphi\).
• (b) Show that \(\varphi\) is harmonic if and only if \(\hbox{div}(\nabla\varphi)=0\).
• (c) Show that if \({\bf F}\) is the gradient of a harmonic function, then \({\bf curl}(F)=0\) and \(\hbox{div}(F)=0\).
• (d) Show that \({\bf F}=\langle xz,-yz,\tfrac12 (x^2-y^2) \rangle\) is the gradient of a harmonic function. What is the flux of \({\bf F}\) through a closed surface?

Question 17.129

Let \({\bf F} = r^n{\bf e}_r \), where \(n\) is any number, \(r=(x^2+y^2+z^2)^{1/2}\), and \({\bf e}_r = r^{-1}\langle x,y,z \rangle\) is the unit radial vector.

• (a) Calculate \(\hbox{div}({\bf F})\).
• (b) Calculate the flux of \({\bf F}\) through the surface of a sphere of radius \(R\) centered at the origin. For which values of \(n\) is this flux independent of \(R\)?
• (c) Prove that \(\nabla(r^n)=n\,r^{n-1}{\bf e}_r\).
• (d) Use (c) to show that \({\bf F}\) is conservative for \(n \ne -1\). Then show that \({\bf F} = r^{-1}{\bf e}_r\) is also conservative by computing the gradient of \(\ln r\).
• (e) What is the value of \(\displaystyle \int_{C} {\bf F}\cdot d{\bf s}\), where \(C\) is a closed curve that does not pass through the origin?
• (f) Find the values of \(n\) for which the function \(\varphi = r^n\) is harmonic.

Question 17.130

Let \(S\) be the boundary surface of a region \(W\) in \({\bf R}^3\) and let \(D_{{\bf e}_{\bf n}}\varphi\) denote the directional derivative of \(\varphi\), where \({\bf e}_{\bf n}\) is the outward unit normal vector. Let \(\Delta\) be the Laplace operator defined earlier.

• (a) Use the Divergence Theorem to prove that \[ \iint_{S\,}D_{{\bf e}_{\bf n}}\varphi \,dS = \iiint_{W\,}\Delta\varphi\,dV \]
• (b) Show that if \(\varphi\) is a harmonic function (defined in Exercise 37), then \[ \iint_{S\,}D_{{\bf e}_{\bf n}}\varphi \,dS = 0 \]

Question 17.131

Assume that \(\varphi\) is harmonic. Show that \(\hbox{div}(\varphi\nabla \varphi)=\|{\nabla \varphi}\|^2\) and conclude that \[ \iint_{S\,} \varphi D_{{\bf e}_{\bf n}}\varphi\,dS = \iiint_{W\,}\|{\nabla \varphi}\|^2\,dV \]

Question 17.132

Let \({\bf F} = \langle P,Q,R\rangle\) be a vector field defined on \({\bf R}^3\) such that \(\hbox{div}({\bf F})=0\). Use the following steps to show that \({\bf F}\) has a vector potential.

• (a) Let \({\bf A} = \langle f, 0, g\rangle\). Show that \[ {\bf curl}({\bf A}) = \langle \dfrac{\partial{g}}{\partial{y}}, \dfrac{\partial{f}}{\partial{z}}-\dfrac{\partial{g}}{\partial{x}},-\dfrac{\partial{f}}{\partial{y}}\rangle \]
• (b) Fix any value \(y_0\) and show that if we define \begin{align*} f(x,y,z) &= -\int_{y_0}^y R(x,t,z)\,dt + \alpha(x,z)\\ g(x,y,z) &= \int_{y_0}^y P(x,t,z)\,dt + \beta(x,z) \end{align*} where \(\alpha\) and \(\beta\) are any functions of \(x\) and \(z\), then \(\partial g/\partial y=P\) and \(-\partial f/\partial y=R\).
• (c) It remains for us to show that \(\alpha\) and \(\beta\) can be chosen so \(Q=\partial f/\partial z-\partial g/\partial x\). Verify that the following choice works (for any choice of \(z_0\)): \[ \alpha(x,z) = \int_{z_0}^z Q(x,y_0,t)\,dt,\qquad \beta(x,z)=0 \] Hint: You will need to use the relation \(\hbox{div}({\bf F})=0\).

Question 17.133

Show that \[{\bf F} = \langle 2y-1, 3z^2, 2xy \rangle\] has a vector potential and find one.

Question 17.134

Show that\[{\bf F} = \langle 2ye^z - xy, y, yz-z\rangle\] has a vector potential and find one.

Question 17.135

In the text, we observed that although the inverse-square radial vector field \(\displaystyle{{\bf F} = \frac{{\bf e}_r}{r^2}}\) satisfies \(\hbox{div}({\bf F})=0\), \({\bf F}\) cannot have a vector potential on its domain \(\{(x,y,z)\ne (0,0,0)\}\) because the flux of \({\bf F}\) through a sphere containing the origin is nonzero.

• (a) Show that the method of Exercise 41 produces a vector potential \({\bf A}\) such that \({\bf F}={\bf curl}({\bf A})\) on the restricted domain \(D\) consisting of \({\bf R}^3\) with the \(y\)-axis removed.
• (b) Show that \({\bf F}\) also has a vector potential on the domains obtained by removing either the \(x\)-axis or the \(z\)-axis from \({\bf R}^3\).
• (c) Does the existence of a vector potential on these restricted domains contradict the fact that the flux of \({\bf F}\) through a sphere containing the origin is nonzero?

Question 17.136

Let \({\bf F}(x,y)= \langle x+ y^2, x^2-y \rangle\) and let \(C\) be the unit circle, oriented counterclockwise. Evaluate \(\displaystyle \oint_{C} {\bf F}\cdot d{\bf s} \) directly as a line integral and using Green’s Theorem.

Question 17.137

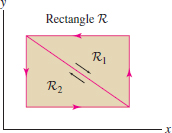
Let \(\partial R\) be the boundary of the rectangle in Figure 17.74 and let \(\partial R_1\) and \(\partial R_2\) be the boundaries of the two triangles, all oriented counterclockwise.

• (a) Determine \(\displaystyle{\oint_{\partial R_1}{\bf F}\cdot d{\bf s}}\) if \(\displaystyle \oint_{\partial R}{\bf F}\cdot d{\bf s}=4\) and \(\displaystyle \oint_{\partial R_2}{\bf F}\cdot d{\bf s}=-2\).
• (b) What is the value of \(\displaystyle{\oint_{\partial R}{\bf F}\,d{\bf s}}\) if \(\partial R\) is oriented clockwise?

Question 17.138

\(\displaystyle{\oint_{C} x y^3 \,dx+ x^3y \,dy}\), where \(C\) is the rectangle \(-1\le x\le 2\), \(-2\le y\le 3\), oriented counterclockwise.

Question 17.139

\(\displaystyle{\oint_{C}(3x+5y- \cos y) \,dx+x \sin y \,dy}\), where \(C\) is any closed curve enclosing a region with area \(4\), oriented counterclockwise.

Question 17.140

\(\displaystyle{\oint_{C} y^2 \,dx- x^2 \,dy}\), where \(C\) consists of the arcs \(y= x^2\) and \(y=\sqrt{x}\), \(0\le x\le 1\), oriented clockwise.

Question 17.141

\(\displaystyle \oint_{C} y e^x \,dx+x e^y \,dy\), where \(C\) is the triangle with vertices \((-1,0)\), \((0,4)\), and \((0,1)\), oriented counterclockwise.

Question 17.142

Let \({\bf c}(t)=\bigl(t^2(1-t),t{(t-1)}^2\bigr)\).

• (a) Plot the path \({\bf c}(t)\) for \(0\le t\le 1\).
• (b) Calculate the area \(A\) of the region enclosed by \({\bf c}(t)\) for \(0\le t\le 1\) using the formula \(\displaystyle{A=\frac12\oint_{C} (x \,dy-y \,dx)}\).

Question 17.143

In (a)–(d), state whether the equation is an identity (valid for all \({\bf F}\) or \( V\)). If it is not, provide an example in which the equation does not hold.

• (a) \({\bf curl}(\nabla V) = 0\)
• (b) \(\hbox{div}(\nabla V) = 0\)
• (c) \(\hbox{div}({\bf curl} ({\bf F})) = 0\)
• (d) \(\nabla (\hbox{div}({\bf F})) = 0\)

Question 17.144

\(\displaystyle{{\bf F}= y{\bf i}-z{\bf k}}\)

Question 17.145

\({\bf F}= \langle e^{x+y}, e^{y+z},xyz \rangle\)

Question 17.146

\(\displaystyle{{\bf F} = \nabla(e^{-x^2-y^2-z^2})}\)

Question 17.147

\(\displaystyle{{\bf e}_r =r^{-1}\langle x, y, z\rangle}\) \(\bigl(r = \sqrt{x^2+y^2+z^2}\bigr)\)

Question 17.148

Recall that if \(F_1\), \(F_2\), and \(F_3\) are differentiable functions of one variable, then \[ {\bf curl} \left(\left< F_1(x), F_2(y), F_3(z) \right>\right)=\mathbf{0} \] Use this to calculate the curl of \[ {\bf F}=\langle x^2+ y^2,\ln y+z^2, z^3\sin(z^2)e^{z^3} \rangle \]

Question 17.149

Give an example of a nonzero vector field \({\bf F}\) such that \({\bf curl}({\bf F})={\bf 0}\) and \(\hbox{div}({\bf F})=0\).

Question 17.150

Verify the identities of Exercises 6 and 13 in Section 17.3 for the vector fields \({\bf F} = \langle xz, ye^x, yz\rangle\) and \({\bf G} = \langle z^2, xy^3, x^2 y\rangle\).

Question 17.151

Suppose that \(S_1\) and \(S_2\) are surfaces with the same oriented boundary curve \(C\). Which of the following conditions guarantees that the flux of \({\bf F}\) through \(S_1\) is equal to the flux of \({\bf F}\) through \(S_2\)?

• (i) \({\bf F} = \nabla V\) for some function \( V\)
• (ii) \({\bf F} = {\bf curl}({\bf G})\) for some vector field \({\bf G}\)

Question 17.152

Prove that if \({\bf F}\) is a gradient vector field, then the flux of \({\bf curl}({\bf F})\) through a smooth surface \(S\) (whether closed or not) is equal to zero.

Question 17.153

Verify Stokes’ Theorem for \({\bf F}= \left< y,z-x,0 \right>\) and the surface \(z=4- x^2- y^2\), \(z\ge 0\), oriented by outward-pointing normals.

Question 17.154

Let \({\bf F}= \langle z^2,x+z, y^2 \rangle\) and let \(S\) be the upper half of the ellipsoid \[{\frac{x^2}{4}+ y^2+ z^2=1}\] oriented by outward-pointing normals. Use Stokes’ Theorem to compute \(\displaystyle{\iint_{S\,}{\bf curl}({\bf F})\cdot d{\bf S}}\).

Question 17.155

Use Stokes’ Theorem to evaluate \(\displaystyle \oint_{C} \langle y,z,x \rangle\cdot d{\bf s} \), where \(C\) is the curve in Figure 17.75.

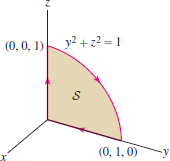
Question 17.156

Let \(S\) be the side of the cylinder \(x^2+y^2=4\), \(0\le z\le 2\) (not including the top and bottom of the cylinder). Use Stokes’ Theorem to compute the flux of \({\bf F}=\langle 0,y, -z\rangle\) through \(S\) (with outward pointing normal) by finding a vector potential \({\bf A}\) such that \({\bf curl}({\bf A})={\bf F}\).

Question 17.157

Verify the Divergence Theorem for \({\bf F}= \langle 0,0,z \rangle\) and the region \(x^2+y^2+z^2=1\).

Question 17.158

\({\bf F} = \langle xy,yz, x^2z+ z^2 \rangle\), \(S\) is the boundary of the box \(\left[0,1\right]\times \left[2,4\right]\times \left[1,5\right]\).

Question 17.159

\({\bf F} = \langle xy,yz, x^2z+ z^2 \rangle\), \(S\) is the boundary of the unit sphere.

Question 17.160

\({\bf F}= \langle xyz+xy,\frac12 y^2(1-z )+ e^x , e^{x^2+ y^2} \rangle\), \(S\) is the boundary of the solid bounded by the cylinder \( x^2+ y^2=16\) and the planes \(z=0\) and \(z=y-4\).

Question 17.161

\({\bf F} = \langle \sin(yz), \sqrt{x^2+z^4}, x\cos(x-y)\rangle\), \(S\) is any smooth closed surface that is the boundary of a region in \({\bf R}^3\).

Question 17.162

Find the volume of a region \(W\) if \[ \iint_{\partial W\,} \langle x+xy+z,x+3y-\frac12y^2,4z \rangle \cdot d{\bf S} =16 \]

Question 17.163

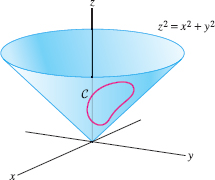
Show that the circulation of \({\bf F} = \langle x^2,y^2,z(x^2+y^2)\rangle\) around any curve \(C\) on the surface of the cone \(z^2= x^2+y^2\) is equal to zero (Figure 17.76).

Question 17.164

Estimate \(\displaystyle{\oint_{C}{\bf F}\cdot d{\bf s}}\), where \(C\) is the circle of radius \(0.03\) in the \(xy\)-plane centered at the origin.

Question 17.165

Estimate \(\displaystyle{\oint_{C}{\bf F}\cdot d{\bf s}}\), where \(C\) is the boundary of the square of side \(0.03\) in the \(yz\)-plane centered at the origin. Does the estimate depend on how the square is oriented within the \(yz\)-plane? Might the actual circulation depend on how it is oriented?

Question 17.166

Suppose that \({\bf v}\) is the velocity field of a fluid and imagine placing a small paddle wheel at the origin. Find the equation of the plane in which the paddle wheel should be placed to make it rotate as quickly as possible.

Question 17.167

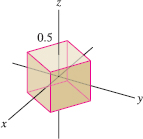
Estimate the flux of \({\bf F}\) through the box of side \(0.5\) in Figure 17.77. Does the result depend on how the box is oriented relative to the coordinate axes?

Question 17.168

The velocity vector field of a fluid (in meters per second) is \[ {\bf F}=\langle x^2+y^2,0,z^2\rangle \] Let \(W\) be the region between the hemisphere \[ S = \bigl\{(x,y,z): x^2+y^2+z^2=1,\quad x,y,z \geq 0\bigr\} \] and the disk \(\displaystyle{D = \bigl\{(x,y,0): x^2+y^2\le 1\bigr\}}\) in the \(xy\)-plane. Recall that the flow rate of a fluid across a surface is equal to the flux of \({\bf F}\) through the surface.

• (a) Show that the flow rate across \(D\) is zero.
• (b) Use the Divergence Theorem to show that the flow rate across \(S\), oriented with outward-pointing normal, is equal to \(\displaystyle{\iiint_{W\,}\hbox{div}({\bf F})\,dV}\). Then compute this triple integral.

Question 17.169

The velocity field of a fluid (in meters per second) is \[ {\bf F} = (3y - 4){\bf i}+ e^{-y(z+1)}{\bf j}+ (x^2 + y^2){\bf k} \]

• (a) Estimate the flow rate (in cubic meters per second) through a small surface \(S\) around the origin if \(S\) encloses a region of volume \(0.01 \mathrm{m^3}\).
• (b) Estimate the circulation of \({\bf F}\) about a circle in the \(xy\)-plane of radius \(r=0.1 \mathrm{m}\) centered at the origin (oriented counterclockwise when viewed from above).
• (c) Estimate the circulation of \({\bf F}\) about a circle in the \(yz\)-plane of radius \(r=0.1 \mathrm{m}\) centered at the origin (oriented counterclockwise when viewed from the positive \(x\)-axis).

Question 17.170

Let \(\displaystyle{ V(x,y)=x+\frac{x}{x^2+y^2}}\). The vector field \({\bf F} = \nabla V\) (Figure 17.78) provides a model in the plane of the velocity field of an incompressible, irrotational fluid flowing past a cylindrical obstacle (in this case, the obstacle is the unit circle \(x^2+y^2=1\)).

• (a) Verify that \({\bf F}\) is irrotational [by definition, \({\bf F}\) is irrotational if \({\bf curl}({\bf F})={\bf 0}\)].
• (b) Verify that \({\bf F}\) is tangent to the unit circle at each point along the unit circle except \((1,0)\) and \((-1,0)\) (where \({\bf F}={\bf 0}\)).
• (c) What is the circulation of \({\bf F}\) around the unit circle?
• (d) Calculate the line integral of \({\bf F}\) along the upper and lower halves of the unit circle separately.

Figure 17.78: The vector field \(\displaystyle{\nabla V}\)

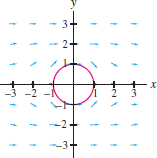
Question 17.171

Figure 17.79 shows the vector field \({\bf F}=\nabla V\), where \[ V(x,y)=\ln\big(x^2+(y-1)^2\big)+\ln\big(x^2+(y+1)^2\big)\] which is the velocity field for the flow of a fluid with sources of equal strength at \((0,\pm 1)\) (note that \( V\) is undefined at these two points). Show that \({\bf F}\) is both irrotational and incompressible—that is, \({\bf curl}_z({\bf F})=0\) and \(\hbox{div}({\bf F})=0\) [in computing \(\hbox{div}({\bf F})\), treat \({\bf F}\) as a vector field in \({\bf R}^3\) with a zero \(z\)-component]. Is it necessary to compute \({\bf curl}_z({\bf F})\) to conclude that it is zero?

Figure 17.79: The vector field \(\displaystyle{\nabla V}\) for \( V(x,y)=\ln(x^2+(y-1)^2)+\ln(x^2+(y+1)^2)\).

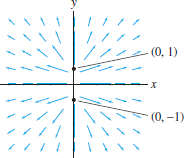
Question 17.172

In Section 17.1, we showed that if \(C\) is a simple closed curve, oriented counterclockwise, then the line integral is \begin{equation} \textrm{Area enclosed by \(C\)} = \frac12\oint_{C} x\,dy-y\,dx\tag{1} \end{equation}

Suppose that \(C\) is a path from \(P\) to \(Q\) that is not closed but has the property that every line through the origin intersects \(C\) in at most one point, as in Figure 17.80. Let \( R\) be the region enclosed by \(C\) and the two radial segments joining \(P\) and \(Q\) to the origin. Show that the line integral in Eq. (1) is equal to the area of \( R\). Hint: Show that the line integral of \({\bf F}=\langle -y,x\rangle\) along the two radial segments is zero and apply Green’s Theorem.

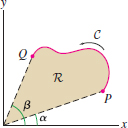
Question 17.173

Suppose that the curve \(C\) in Figure 17.80 has the polar equation \(r=f(\theta)\).

• (a) Show that \({\bf c}(\theta)=(f(\theta)\cos\theta, f(\theta)\sin\theta)\) is a counterclockwise parametrization of \(C\).

  1044

• (b) In Section 11.4, we showed that the area of the region \( R\) is given by the formula \[ \textrm{Area of \( R\)} = \frac12\int_{\alpha}^{\beta}f(\theta)^2\,d\theta \] Use the result of Exercise 37 to give a new proof of this formula. Hint: Evaluate the line integral in Eq. (1) using \({\bf c}(\theta)\).

Question 17.174

Prove the following generalization of Eq. (1). Let \(C\) be a simple closed curve in the plane (Figure 17.81) \[ S:\quad ax+by+cz+d=0 \] Then the area of the region \(R\) enclosed by \(C\) is equal to \[ \frac{1}{2\|{{\bf n}}\|} \oint_{C} (bz-cy) \,dx+(cx-az) \,dy+(ay-bx) \,dz \] where \({\bf n}=\langle a, b, c\rangle\) is the normal to \(S\), and \(C\) is oriented as the boundary of \( R\) (relative to the normal vector \({\bf n}\)). Hint: Apply Stokes’ Theorem to \(\displaystyle{{\bf F} = \langle bz-cy,cx-az,ay-bx \rangle}\).

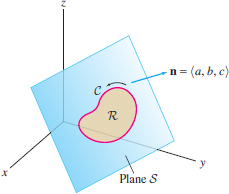
Question 17.175

Use the result of Exercise 37 to calculate the area of the triangle with vertices \((1,0,0)\), \((0,1,0)\), and \((0,0,1)\) as a line integral. Verify your result using geometry.

Question 17.176

Show that \(G(\theta,\phi)= (a\cos\theta\sin\phi,b\sin\theta\sin\phi,c\cos\phi)\) is a parametrization of the ellipsoid \[ \left(\frac{x}a\right)^2+\left(\frac{y}b\right)^2+\left(\frac{z}c\right)^2 = 1 \] Then calculate the volume of the ellipsoid as the surface integral of \({\bf F} = \frac13\langle x,y,z\rangle\) (this surface integral is equal to the volume by the Divergence Theorem).