exercises
In Exercises 1 to 8, sketch the given vector field or a small multiple of it.
Question 13.250
\({\bf F}(x,y)=(2,2)\)
Question 13.251
\({\bf F}(x,y)=(4,0)\)
Question 13.252
\({\bf F}(x,y)=(x,y)\)
Question 13.253
\({\bf F}(x,y)=(-x,y)\)
Question 13.254
\({\bf F}(x,y)=(2y,x)\)
Question 13.255
\({\bf F}(x,y)=(y,-2x)\)
Question 13.256
\({\bf F}(x,y)=\bigg(\displaystyle\frac{x}{\sqrt{x^2+y^2}},\displaystyle\frac{y}{\sqrt{x^2+y^2}}\bigg)\)
Question 13.257
\({\bf F}(x,y)=\bigg(\displaystyle\frac{y}{\sqrt{x^2+y^2}},\displaystyle\frac{x}{\sqrt{x^2+y^2}}\bigg)\)
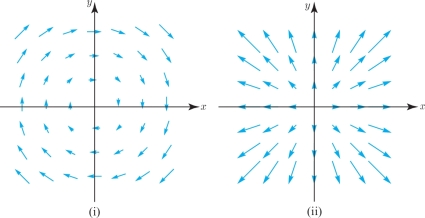
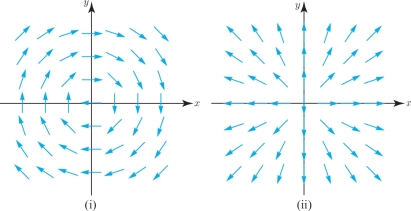
In the following two exercises, match the given vector field with its pictorial description (see Figure 13.28 and Figure 13.29).
Question 13.258
- (a) \(\textbf{V}(x,y) = x \textbf{i} + y \textbf{j}\)
- (b) \(\textbf{V}(x,y) = y \textbf{i} - x \textbf{j}\)
Question 13.259
- (a) \(\textbf{V}(x,y) = \displaystyle\frac{y}{\sqrt{x^2 + y^2}} \textbf{i} - \displaystyle\frac{x}{\sqrt{x^2 + y^2}} \textbf{j}\)
- (b) \(\textbf{V}(x,y) = \displaystyle\frac{x}{\sqrt{x^2 + y^2}} \textbf{i} + \displaystyle\frac{y}{\sqrt{x^2 + y^2}} \textbf{j}\)
Where are these vector fields not defined? How are these vector fields related to those in Problem 9?
In Exercises 11 to 14, sketch a few flow lines of the given vector field.
Question 13.260
\({\bf F}(x,y)=(y,-x)\)
Question 13.261
\({\bf F}(x,y)=(x,-y)\)
Question 13.262
\({\bf F}(x,y)=(x,x^2)\)
Question 13.263
\({\bf F}(x,y,z)=(y,-x,0)\)
244
In Exercises 15 to 18, show that the given curve \({\bf c}(t)\) is a flow line of the given velocity vector field \({\bf F}(x,y,z)\).
Question 13.264
\({\bf c}(t)=(e^{2t},\log |t|,1/t),t\neq 0; {\bf F}(x,y,z)=(2x,z,-z^2)\)
Question 13.265
\({\bf c}(t)=(t^2,2t-1,\sqrt{t}),t > 0 ;{\bf F}(x,y,z)=(y+1,2,1/2z)\)
Question 13.266
\({\bf c}(t)=(\sin t,\,\cos t,e^t);{\bf F}(x,y,z)=(y,-x,z)\)
Question 13.267
\({\bf c}(t)=(\displaystyle\frac{1}{t^3},e^t,\displaystyle\frac{1}{t});{\bf F}(x,y,z)=(-3z^4,y,-z^2)\)
Question 13.268
Let \(\textbf{F}(x,y,z)=(x^2,yx^2,z+zx)\) and \(\textbf{c}(t)= (\displaystyle\frac{1}{1-t},0,\displaystyle\frac{e^t}{1-t})\). Show \(\textbf{c}(t)\) is a flow line for \(\textbf{F}\).
Question 13.269
Show that \(\textbf{c}(t)=(a\cos t-b \sin t, a \sin t +b\cos t)\) is a flow line for \(\textbf{F}(x, y)=(-y, x)\) for all real values of \(a\) and \(b\).
Question 13.270
- (a) Let \(\textbf{F}(x, y, z)= (yz, xz, xy)\). Find a function \(f \colon \mathbb R^3 \to \mathbb R\) such that \(\textbf{F}=\nabla f\).
- (b) Let \(\textbf{F}(x, y, z)= (x, y, z)\). Find a function \(f \colon \mathbb R^3 \to \mathbb R\) such that \(\textbf{F}=\nabla f\).
Question 13.271
Let \(f(x, y)=x^2+y^2\). Sketch the gradient vector field \(\nabla f\) together with some level sets of \(f\). How are they related?
Question 13.272
Show that it takes half as much energy to launch a satellite into an orbit just above the earth as it does to escape the earth. (Ignore the rotation of the earth.)
Question 13.273
Let \({\bf c}(t)\) be a flow line of a gradient field \({\bf F}=-{\nabla} V\). Prove that \(V({\bf c}(t))\) is a decreasing function of \(t\).
Question 13.274
Suppose that the isotherms in a region are all concentric spheres centered at the origin. Prove that the energy flux vector field points either toward or away from the origin.
Question 13.275
Sketch the gradient field \(-{ \nabla} V\) for \(V(x,y)=(x+y)/(x^2+y^2)\) and the equipotential surface \(V=1\).
Question 13.276
Let \(\textbf{F}(x, y, z)= (xe^y, y^2z^2, xyz)\) and suppose \(\textbf{c}(t)=\big(x(t), y(t), z(t)\big)\) is a flow line for \(\textbf{F}\). Find the system of differential equations that the functions \(x(t), y(t),\) and \(z(t)\) must satisfy.