Question 3.1

\(f(x,y)=2xy/(x^2+y^2)^2\), on the region where \((x,y)\neq (0,0)\)

Question 3.2

\(f(x,y,z)\,{=}\,e^z \,{+}\, (1/x) \,{+}\, xe^{-y}\), on the region where \(x\,{\neq}\, 0\)

Question 3.3

\(f(x,y)=\cos\, (xy^2)\)

Question 3.4

\(f(x,y)=e^{-xy^{2}}+y^3x^4\)

Question 3.5

\(f(x,y)=1/(\cos^2 x+e^{-y})\)

Question 3.6

\(f(x,y)\,{=}\,\log\,(x-y)\)

Question 3.7

Find all second partial derivatives of the following functions at the point \(\textbf{x}_0\).

• (a) \(f(x, y)= \sin(xy); \ \textbf{x}_0=(\pi, 1) \)
• (b) \(f(x, y)= xy^8+x^2+y^4; \ \textbf{x}_0=(2, -1) \)
• (c) \(f(x, y, z)=e^{xyz} ; \ \textbf{x}_0=(0, 0, 0) \)

Question 3.8

Find all second partial derivatives of \(f(x, y)= \sec^3(4y-3x)\).

157

Question 3.9

Can there exist a \(C^2\) function \(f(x, y)\) with \(f_x=2x-5y\) and \(f_y=4x+y\)?

Question 3.10

The heat conduction equation is \(u_t=ku_{xx}\). Determine whether \(u(x, t)=e^{-kt}\sin(x)\) is a solution.

Question 3.11

Show that the following functions satisfy the one-dimensional wave equation \[ \frac{\partial^2f}{\partial x^2}= \frac{1}{c^2}\frac{\partial^2f}{\partial t^2}. \]

• (a) \(f(x,t)=\sin(x-ct)\)
• (b) \(f(x,t)=\sin (x) \sin(ct)\)
• (c) \(f(x, t)= (x-ct)^6 + (x+ct)^6\)

Question 3.12

• (a) Show that \(T(x, t)=e^{-kt}\cos x\) satisfies the one-dimensional heat equation \[ k\frac{\partial^2T}{\partial x^2}= \frac{\partial T}{\partial t}. \]
• (b) Show that \(T(x, y, t)=e^{-kt} (\cos x +\cos y)\) satisfies the two-dimensional heat equation \[ k\Big(\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}\Big)= \frac{\partial T}{\partial t}. \]
• (c) Show that \(T(x, y, z, t)=e^{-kt}(\cos x + \cos y+\cos z)\) satisfies the three-dimensional heat equation \[ k\Big(\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}+\frac{\partial^2T}{\partial z^2}\Big)= \frac{\partial T}{\partial t}. \]

Question 3.13

Find \(\partial^2 z/\partial x^2,\partial^2 z/\partial x\,\partial y, \partial^2 z/\partial y\,\partial x\), and \(\partial^2z/\partial y^2\) for

• (a) \(z=3x^2+2y^2\)
• (b) \(z=(2x^2+7x^2y)/3xy\), on the region where \(x\neq 0\) and \(y\neq 0\)

Question 3.14

Find all the second partial derivatives of

• (a) \(z=\sin\,(x^2-3xy)\)
• (b) \(z=x^2y^2e^{2xy}\)

Question 3.15

Find \(f_{xy},f_{yz},f_{zx}\), and \(f_{xyz}\) for \[ f(x,y,z)=x^2y+xy^2+yz^2. \]

Question 3.16

Let \(z=x^4y^3-x^8+y^4\).

• (a) Compute \(\partial^3 z/\partial y\,\partial x\, \partial x,\partial^3 z/\partial x\, \partial y\, \partial x,\) and \(\partial^3 z/\partial x\, \partial x\, \partial y\) (also denoted \(\partial^3 z/\partial x^2 \partial y\)).
• (b) Compute \(\partial^3 z/\partial x\,\partial y\, \partial y,\partial^3 z/\partial y\, \partial x\, \partial y,\) and \(\partial^3 z/\partial y\, \partial y\, \partial x\) (also denoted \(\partial^3 z/\partial y^2 \partial x\)).

Question 3.17

Use Theorem 1 to show that if \(f(x,y,z)\) is of class \(C^3\), then \[ \frac{\partial^3\! f}{\partial x\,\partial y\,\partial z}=\frac{\partial^3\! f}{\partial y\,\partial z\,\partial x}. \]

Question 3.18

Verify that \[ \frac{\partial^3\! f}{\partial x\, \partial y\,\partial z}=\frac{\partial^3\! f}{\partial z\,\partial y\,\partial x} \] for \(f(x,y,z)=ze^{xy}+yz^3x^2\).

Question 3.19

Verify that \(f_{xzw}=f_{zwx}\) for \(f(x,y,z,w)=e^{\,xyz}\sin\,(xw)\).

Question 3.20

If \(f(x, y, z, w)\) is of class \(C^3\), show that \(f_{xzw}=f_{zwx}\).

Question 3.21

Evaluate all first and second partial derivatives of the following functions:

• (a) \(f(x,y)=x\,{\rm arctan}\,(x/y)\)
• (b) \(f(x,y)=\cos \sqrt{x^2+y^2}\)
• (c) \(f(x,y)=\exp\,(-x^2-y^2)\)

Question 3.22

Let \(w=f(x,y)\) be a function of two variables and let \(x=u+v,y=u-v\). Show that \[ \frac{\partial^2 w}{\partial u\,\partial v}=\frac{\partial^2 w} {\partial x^2}-\frac{\partial^2 w}{\partial y^2}. \]

Question 3.23

Let \(f{:}\, \,{\mathbb R}^2 \rightarrow {\mathbb R}\) be a \(C^2\) function and let \({\bf c}(t)\) be a \(C^2\) curve in \({\mathbb R}^2\). Write a formula for the second derivative \((d^2{/}dt^2)((f\circ {\bf c})(t))\) using the chain rule twice.

Question 3.24

Let \(f(x,y,z)=e^{\,xz}\tan\,(yz)\) and let \(x=g(s,t)\), \(y=h(s,t),z=k(s,t)\), and define the function \(m(s,t)=f(g(s,t)\), \(h(s,t),k(s,t))\). Find a formula for \(m_{st}\) using the chain rule and verify that your answer is symmetric in \(s\) and \(t\).

Question 3.25

A function \(u=f(x,y)\) with continuous second partial derivatives satisfying Laplace’s equation \[ \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0 \] is called a harmonic function. Show that the function \(u(x,y)=x^3-3xy^2\) is harmonic.

Question 3.26

Which of the following functions are harmonic? (See Exercise 25.)

• (a) \(f(x,y)=x^2-y^2\)
• (b) \(f(x,y)=x^2+y^2\)
• (c) \(f(x,y)=xy\)
• (d) \(f(x,y)=y^3+3x^2y\)
• (e) \(f(x,y)=\,\sin x\cosh y\)
• (f) \(f(x,y)=e^x\,\sin y\)

158

Question 3.27

• (a) Is the function \(f(x, y, z)=x^2-2y^2+z^2\) harmonic? What about \(f(x, y, z)=x^2+y^2-z^2\)?
• (b) Laplace’s equation for functions of \(n\) variables is \[ \frac{\partial^2f}{\partial x_1^2} +\frac{\partial^2f}{\partial x_2^2} + \cdots +\frac{\partial^2f}{\partial x_n^2} =0. \]

Find an example of a function of \(n\) variables that is harmonic, and show that your example is harmonic.

Question 3.28

Show that the following functions are harmonic:

• (a) \(f(x, y)= \arctan \frac{y}{x}\)
• (b) \(f(x, y) = \log (x^2 +y^2)\)

Question 3.29

Let \(f\) and \(g\) be \(C^2\) functions of one variable. Set \(\phi=f(x-t)+g(x+t)\).

• (a) Prove that \(\phi\) satisfies the wave equation: \(\partial^2 \phi /\partial t^2=\partial^2 \phi/\partial x^2\).
• (b) Sketch the graph of \(\phi\) against \(t\) and \(x\) if \(f(x)=x^2\) and \(g(x)=0\).

Question 3.30

• (a) Show that function \(g(x,t)=2+e^{-t} \sin x\) satisfies the heat equation: \(g_t=g_{xx}\). [Here \(g(x,t)\) represents the temperature in a metal rod at position \(x\) and time \(t\).]
• (b) Sketch the graph of \(g\) for \(t\geq 0\). (HINT: Look at sections by the planes \(t=0,t=1\), and \(t=2\).)
• (c) What happens to \(g(x,t) \hbox{ as } t\rightarrow \infty\)? Interpret this limit in terms of the behavior of heat in the rod.

Question 3.31

Show that Newton’s potential \(V=-GmM/r\) satisfies Laplace’s equation \[ \frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+ \frac{\partial^2 V}{\partial z^2}=0\quad \hbox{for}\quad (x,y,z)\neq (0,0,0). \]

Question 3.32

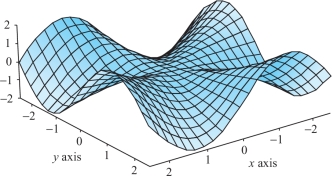
Let \[ f(x,y)=\Big\{\begin{array}{l@{\quad}l} xy(x^2-y^2)/(x^2+y^2), & (x,y)\neq (0,0)\\[2pt] 0, & (x,y)=(0,0) \end{array} \] (see Figure 3.4).

• (a) If \((x,y)\neq (0,0)\), calculate \(\partial f/\partial x\) and \(\partial f/\partial y\).
• (b) Show that \((\partial f/ \partial x)(0,0)=0=(\partial f/ \partial y)(0,0)\).
• (c) Show that \((\partial^2 \! f/ \partial x\,\partial y)(0,0)= 1, (\partial^2\! f/\partial y\, \partial x)(0,0)=-1\).
• (d) What went wrong? Why are the mixed partials not equal?