Practicing Geology Exercise
The Principle of Isostasy: Why Are Oceans Deep and Mountains High?
Earth’s topography is dominated by continents, which typically have elevations of 0 to 1 km above sea level, and ocean basins, which typically have elevations of 4 to 5 km below sea level. Why the difference? The answer comes from the principle of isostasy, which relates the elevations of continents and oceans to the densities of crustal and mantle rocks. This amazingly useful principle not only explains much of Earth’s topography, but also allows scientists to use changes in crustal elevation over time to investigate the properties of the mantle (see Earth Issues 14.1).
Isostasy (from the Greek for “equal standing”) is based on Archimedes’ principle, which states that the weight of a floating solid is equal to the weight of the fluid it displaces. (According to legend, the Greek philosopher Archimedes discovered this principle over 2200 years ago while sitting in his bath; boggled by its implications, he rushed naked into the street, yelling “Eureka, I have found it!” Major discoveries rarely provoke such enthusiastic responses from modern scientists.)
Consider a block of wood floating in water. In each unit of area, the block’s mass is its density times its thickness, whereas the mass of the water it displaces is the density of water times a reduced thickness, given by the block’s thickness minus its elevation above the water. Archimedes’ principle states that these two must be equal:
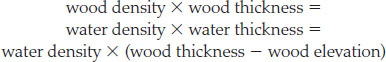
We can solve the last algebraic equation to find the elevation:

The expression in brackets is called the “buoyancy factor” because it tells us what fraction of the wood will rise above the water surface. A light wood, such as young pine, has only half the density of water, so its buoyancy factor is
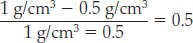
The pine block will float high, with half of its volume out of the water. However, in the case of old oak, which has a density of 0.9 g/cm3, the buoyancy factor is only 0.1, so the block will float low, with only one-tenth of its thickness above the water.
If continental crust (density 5 2.8 g/cm3) floated alone on top of mantle material (3.3 g/cm3), the previous equation could be modified to give continental elevation by simply replacing “wood” with “continent” and “water” with “mantle.” However, we must account for the oceanic crust (2.9 g/cm3) and the ocean water (1.0 g/cm3) that also float on the mantle. Since these two layers fill up the basins around the continents, we must subtract from the continental elevation the height that each of those layers alone would float above the mantle, given by its buoyancy factor times its thickness. The isostatic equation for continents therefore has three terms, one positive and two negative:
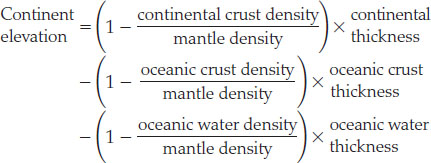
Using thicknesses of 33 km and 7 km for continental and oceanic crust, respectively, and a water depth of 4.5 km, we obtain
405
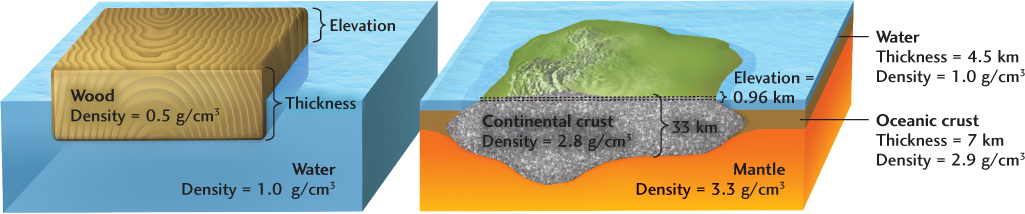
continent elevation

This result is consistent with the overall distribution of Earth’s topography (see Figure 1.8).
Because of isostasy, elevation is a sensitive indicator of crustal thickness, so regions of lower elevation must have thinner crust (or higher average density), whereas regions of higher elevation, such as the Tibetan Plateau (see Figure 10.16), must have thicker crust (or lower average density).
BONUS PROBLEM: The average elevation of the Tibetan Plateau is about 5 km above sea level. Use the isostatic equation to compute the average thickness of the crust in this region, assuming that its average density is 2.8 g/cm3.