Practicing Geology Exercise
How Much Water Can Our Well Produce?
The most important question anyone who is considering drilling a well can ask is whether that well will produce enough water to satisfy their needs. A well drilled in one kind of formation might produce plenty of water, while another not far away, but in a different formation, might not. How can we predict groundwater behavior well enough to know how much water a well in a certain location will produce?
Henri Darcy was able to turn his conceptual understanding of the principles of groundwater flow into a simple and very useful mathematical equation. This equation—Darcy’s law—shows how geologic factors control the rate of water flow through an aquifer:
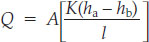
What this equation says is that the volume of water flowing in a certain time (Q) is proportional to the cross- sectional area of the aquifer through which the volume of water flows (A); the hydraulic conductivity of the aquifer, a measure of the permeability of the rock or soil that composes it (K); and the hydraulic gradient. The hydraulic gradient can be determined by installing test wells at two points, a and b, measuring the difference in the elevation of the water table between them (ha − hb), and then dividing the result by the distance between them (l). The water flow will increase if the cross-sectional area of the aquifer increases, if the hydraulic gradient increases, or if the hydraulic conductivity increases.
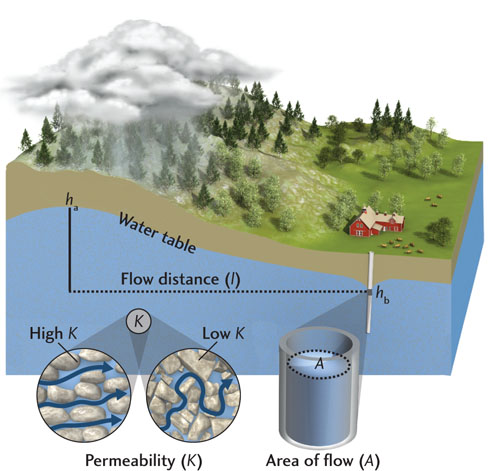
In rural and many suburban parts of the United States, it is still common practice to drill wells for the family water supply. When choosing a home site, a family must be careful to take into account the geology of the site and whether it is suitable for sufficient water flow. Will the water flowing through the well at point B in the accompanying diagram produce enough water for a family’s needs? It depends on a number of factors, including the type of formation in which the well is drilled. We can use Darcy’s law to evaluate the effects of hydraulic conductivity on the amount of water that will flow through the well.
Using the measurements provided in the diagram, we find the following values:
Cross-sectional area of well pipe = A = 0.25 m2

Next, we find the value of Q for different values of K representing different Earth materials: clay, silty sand, well-sorted sand, and well-sorted gravel.
| Material | Hydraulic conductivity (K) |
|---|---|
| Clay | 0.001 m/day |
| Silty sand | 0.3 m/day |
| Well-sorted sand | 40 m/day |
| Well-sorted gravel | 3750 m/day |
497
Now we can use Darcy’s law to determine Q for well-sorted sand:
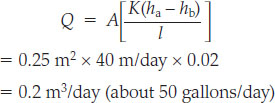
and for clay:
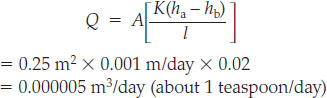
It is clear based on these calculations that if the well has been drilled in well-sorted sand, it might provide just enough water for a family of four, assuming each person uses 10 gallons per day for drinking, showering, toilet use, cooking, cleaning, and yard maintenance. In contrast, if the well has been drilled in clay, it is likely to be a severe disappointment.
BONUS PROBLEM: Use Darcy’s law to find the volume of water that could flow through the well in one day if it were drilled in silty sand or in well-sorted gravel.
Flow velocities calculated by Darcy’s law have been confirmed experimentally by measuring how long it takes a harmless dye introduced into one well to reach another well. In most aquifers, groundwater moves at a rate of a few centimeters per day. In very permeable gravel beds near the surface, groundwater may travel as much as 15 cm/day. (This speed is still much slower than the speeds of 20 to 50 cm/s typical of river flows.)