Practicing Geology Exercise

How Fast Do Streams Erode Bedrock?

In mountainous regions, the flowing water in streams cuts downward into bedrock that is uplifted by tectonic processes. It is hard to imagine that something as hard as rock could be cut by flowing water! The purpose of this exercise is to learn how to measure the rate of this erosion, which can be surprisingly fast.

The rate of erosion depends on how quickly the water flows and on how much sediment is suspended in the flowing water. The erosion of stream channels cut into bedrock is the result of the plucking of large pieces of rock and of abrasion by sediment particles. Plucking of rock occurs most readily when the bedrock is penetrated by tightly spaced sets of fractures or consists of sedimentary rocks with well-defined, closely spaced bedding planes. The zones of weakness inherent in such rocks allow blocks to be broken off the streambed and transported downstream; once loose, the moving blocks can strike other projecting rocks and break them loose as well. Abrasion occurs when sediment particles impact the bedrock and break tiny pieces—smaller than the size of the impacting grain—from the bedrock. While this effect is trivially small on a grain-by-grain basis, it becomes very important when the effects of millions of impacting grains are added up. This is important because the rate of bedrock erosion is what controls the aesthetic beauty of the most dramatic landscapes on Earth, such as the Sierra Nevada mountains, the Grand Tetons, the Alps, and the Himalaya.

Flow velocity is also extremely important. Observations in both the field and the laboratory show that the erosion rate depends on the velocity of the flow raised to the fifth power (erosion rate €V⁵). This means that small increases in current velocity cause dramatic increases in erosion rates. Simply doubling the flow velocity might increase the erosion rate 30 times over what it was initially; double it again and the erosion rate might increase 1000 times over what it was initially. Therefore, it is during rare but powerful flows, such as floods, that the current is capable of eroding bedrock; most of the rest of the time, little erosion occurs.

To understand bedrock erosion, geologists study high-mountain streams such as the Indus River in northern Pakistan. The Indus is one of the world’s largest rivers, and it cuts through the heart of Earth’s tallest mountain ranges: the Himalaya, Karakoram, and Hindu Kush. Its discharge is 6600 m³/s—enough to fill an average two-story house six times every second! Where the river passes through Nanga Parbat—forming a very narrow and deep gorge—this extremely high discharge results in some of the highest erosion rates on Earth. There, the river is narrow and its slope is steep; thus, current velocities are high—and bedrock erosion rates are high.

Geologists measure bedrock erosion rates using several methods. The most straightforward is to create markers, such as drill holes, on the bottom of a river channel and then monitor the changes in those markers over time. Holes are drilled to a known depth; then, at the end of a specified period—say, after a year—the decrease in the hole depth is measured. This method yields an erosion rate representing an average of all rates during that year, including shorter periods when erosion rates were higher or lower.

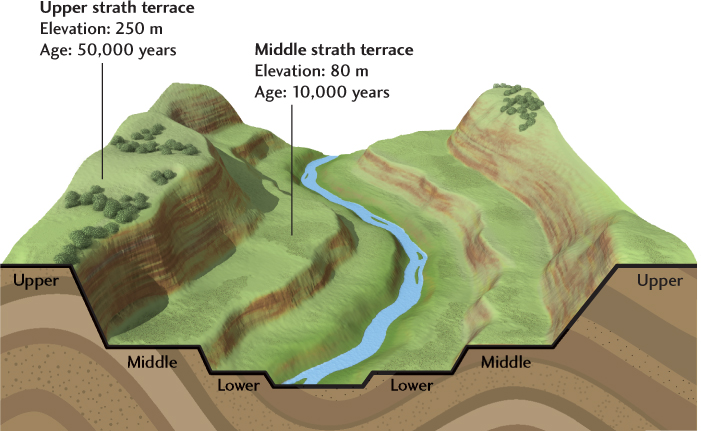
Erosion rates are harder to measure over longer periods. Geologists often search for strath terraces preserved along the slopes that lead down into river channels. Strath terraces are topographic benches carved in bedrock, and sometimes overlain by gravel deposits, that mark the former positions of the river channel bottom. They are preserved as the river cuts down to new levels. If the age of a strath terrace and its height above the current streambed can both be measured, then the long-term erosion rate can be calculated. Ages of strath terraces are commonly measured using the beryllium-10 method mentioned later in this chapter.

In the accompanying diagram, each of two strath terraces is labeled with an age and a corresponding elevation. For the lower terrace, with an age of 10,000 years and an elevation of 80 m above the streambed, the long-term erosion rate is given by

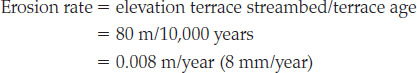
BONUS PROBLEM: What is the long-term erosion rate represented by the upper strath terrace?