Practicing Geology Exercise

How Do Valuable Metallic Ores Form? Magmatic Differentiation Through Crystal Setting

Some of the most economically important mineral deposits in the world are formed by differential settling of crystals in magma chambers. The Bushveld deposit in South Africa and the Stillwater deposit in Montana, just north of Yellowstone National Park, are two of the most famous examples. These deposits contain some of the world’s largest reserves of metals in the platinum group—such as platinum and palladium—but vast quantities of iron, tin, chromium, and titanium are also found there. These deposits represent ancient magma chambers in which fractional crystallization led to the formation of different minerals over time, which settled to the bottom of the magma chamber in economically important concentrations. Geologists realized that the process of crystal settling was the key to understanding how the deposits formed.

Many geologic processes involve the movement of particles within fluids. We see the same basic principles in the movement of sand grains in rivers, in the hurtling of debris through the atmosphere when a volcano erupts, and in the settling of crystals through magmas. In each case, the movement of the particles is regulated by a number of factors.

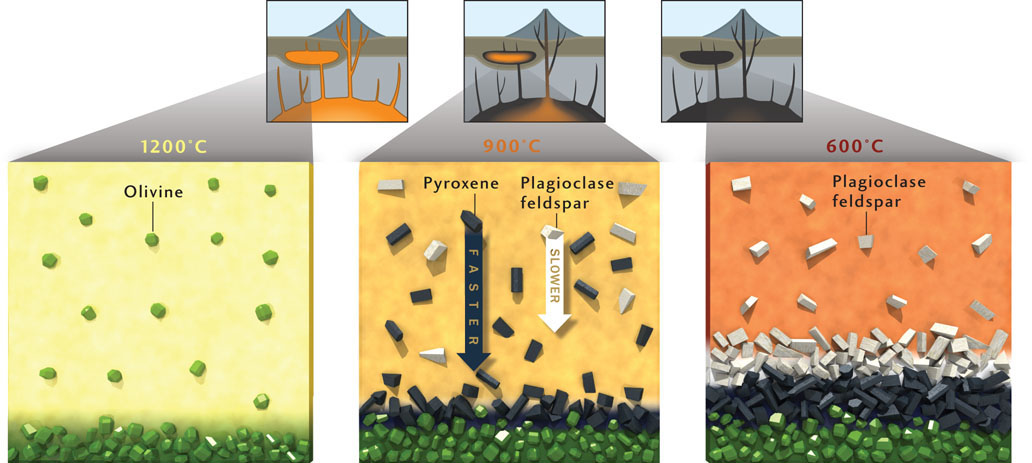
In the example of the Palisades sill, we saw that as a basaltic magma cools, olivine crystallizes first, followed by pyroxene and plagioclase feldspar. Once crystallized, each mineral sinks through the remaining liquid magma to settle out at the bottom of the magma chamber. Thus, the Palisades sill is layered with olivine at its base, followed by pyroxene and plagioclase feldspar overlying it (see Figure 4.7).

Olivine not only crystallizes before feldspar, but also settles more quickly than feldspar due to its higher density. Both fractional crystallization and crystal settling rates contribute to the segregation of minerals within magma chambers.

The rate at which crystals settle depends both on their density and size and on the viscosity of the remaining magma. That rate can be calculated using a mathematical relationship called Stokes’ law:

where V is the velocity at which the crystals settle through the magma; g is the acceleration due to Earth’s gravity (980 cm/s²); r is the radius of the crystal; d_c is the density of the crystal; d_m is the density of the magma; and u is the viscosity of the magma.

Stokes’ law states that three factors are important in regulating the velocity at which crystals will move through magma:

• 1. As crystals grow larger, their radius (r) increases. Because r is in the numerator of the equation, Stokes’ law tells us that larger crystals will settle faster than smaller crystals. Furthermore, r is squared, which tells us that small increases in crystal size will result in much larger increases in their settling velocity.
• 2. Magma viscosity (u) is a measure of the resistance of the magma to flow or, in this case, to moving out of the way of a sinking crystal. Because u is in the denominator of the equation, it tells us that an increase in magma viscosity will result in a decrease in settling velocity.
• 3. Settling velocity (V) also depends on the difference between the density of the crystal (d_c) and the density of the magma (d_m). V will increase as the density of the crystal increases and as the density of the magma decreases. Thus, in a magma of constant density, crystals with higher density will settle faster than crystals with lower density.

If we now consider fractional crystallization in the Palisades sill, Stokes’ law will help us determine the actual settling rates for particular minerals. Consider an olivine crystal with a radius of 0.1 cm and a density of 3.7 g/cm³. The magma through which the crystal settles has a density of 2.6 g/cm³ and a viscosity of 3000 poise (1 poise = 1 g/cm ✕ s). How fast will this olivine crystal fall through the magma?

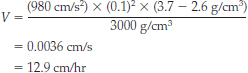
BONUS PROBLEM: Try the same calculation for a plagioclase feldspar crystal of the same size, which has a density of 2.7 g/cm³. Which mineral settles through the magma at a faster rate? How much faster does it settle?