Practicing Geology Exercise
How Do Isotopes Tell Us the Ages of Earth Materials?
Isotopic dating methods allow us to date many types of Earth materials for many practical purposes: rock formations in the search for minerals and petroleum; water samples to understand oceanic circulation; ice cores to chart climate variations; and even bubbles of air trapped in rocks and ice to measure changes in the composition of the atmosphere. So it’s worthwhile to understand in more detail how geologists actually determine the ages of materials using isotopes.
Consider a mineral grain that was formed at time T = 0 and contains a certain amount of a parent isotope—say, 1000 atoms. If we measure the age of the mineral grain in half-lives of the parent isotope, the amount left at any age T will be 1000 × 1/2T. In other words, in one half-life—that is, when T = 1—the initial amount of the parent isotope will be reduced to 1/21 = 1/2 (500 atoms); in two half-lives, to 1/22 = 1/4 (250 atoms); in three half-lives, to 1/23 = 1/8 (125 atoms); and so on (see Figure 8.13).
The radioactive decay of each atom of the parent isotope generates one new atom of the daughter isotope. If the mineral grain remains a closed system (that is, if no isotopes are transferred into or out of the grain), the number of new daughter atoms produced from the parent atoms by age T must equal 1000 × (1 2 1/2T), because the new daughters and remaining parents must add up to the initial amount of the parent isotope (1000 atoms). The ratio of new daughters to remaining parents thus depends only on the age of the mineral grain:
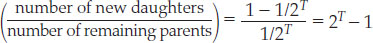
As the age of the mineral grain increases from 0 to 3 half-lives, for instance, this ratio increases from 0 to 7, independently of the initial number of parent atoms.
With a mass spectrometer, we can measure the parent and daughter isotopes precisely: today, such instruments can literally count the atoms in a small sample. But to determine the age of a mineral grain, we must account for any daughter isotope incorporated into the mineral grain at the time it crystallized. In our example, if there were 100 daughter atoms in the grain at T = 0, then the number of daughter atoms would increase to 500 + 100 = 600 after one half-life; to 750 + 100 = 850 after two half-lives; and to 875 + 100 = 975 after three half-lives. The general expression for the total number of daughter atoms is therefore
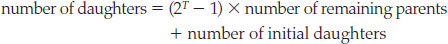
217
You may notice that this is an equation for a straight line with a slope of (2T − 1) and an intercept equal to the initial number of daughter atoms, as illustrated in part (a) of the accompanying illustration.
Although we can measure only the total amount of the daughter isotope, we can often infer the initial amount from another isotope of the same element. For example, strontium-87 is created by the decay of rubidium-87 (see Figure 8.13), but another isotope, strontium-86, is not produced by radioactive decay and is not itself radioactive. Thus, if a mineral grain remains a closed system after crystallization, the number of strontium-86 atoms will not change with age. The trick is to divide the daughter-parent relationship by the amount of strontium-86:
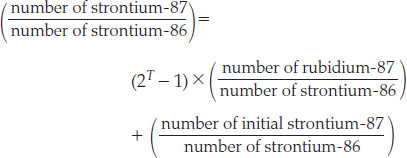
Different mineral grains in a rock will crystallize with differing initial amounts of strontium and rubidium. However, because the two strontium isotopes behave similarly in the chemical reactions that take place before crystallization, the strontium-87/strontium-86 ratio at crystallization will be the same for all the grains in the same rock. Therefore, by fitting a line to the data from several mineral grains, we can determine the initial strontium-87/strontium-86 ratio as well as the age T.
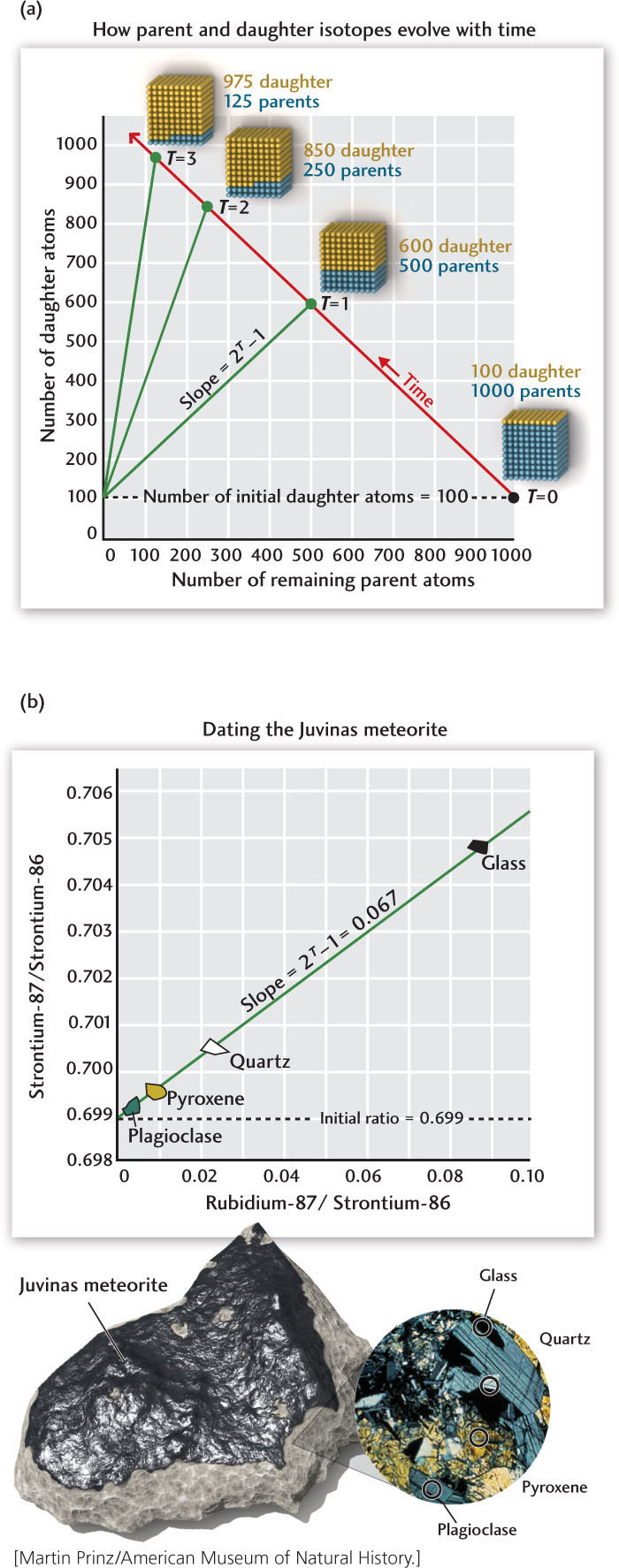
In part (b) of the accompanying figure, we apply this method to strontium and rubidium measurements from a famous stony meteorite, called Juvinas, that fell in southern France in 1821. The Juvinas meteorite, which is similar to the one shown in Figure 1.10a, is thought to have come from a planetary body that formed at the same time as Earth but was subsequently destroyed by planetary collisions (see Chapter 9). Using mass spectrometer measurements of four samples from this meteorite, we can plot the strontium-87/strontium-86 and rubidium-87/strontium-86 ratios along a line whose intercept gives an initial strontium-87/strontium-86 ratio of 0.699. That line is an isochron (a locus of equal time) with a slope of 0.067.
218
To solve for T, we begin with
(2T − 1) = 0.067
Adding 1 to both sides of this equation and taking base-10 logarithms of both sides yields
T log(2) = log(1.067)
or
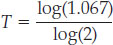
Using a scientific calculator (there’s probably one on your smart phone), we find that log(1.067) = 0.0282 and log(2) = 0.301, which gives
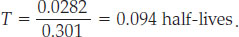
Multiplying the number of half-lives by the half-life of rubidium-87, 49 billion years (see Table 8.1), yields a meteorite age of
0.094 × 49 billion years = 4.59 billion years
The uncertainty of this estimate is about 0.07 billion years, so it’s consistent with the age of 4.56 billion years first obtained for Earth by Patterson in 1956.
BONUS PROBLEM: When plotted on a diagram like part (b) of the accompanying figure, the rubidium and strontium isotope ratios from several mineral grains collected from the same rock lie on a line with a slope of 0.0143. Assuming these mineral grains have been closed systems since they crystallized, calculate the age of the rock. Hint: log(1.0143) = 0.00617.