TOOLS OF THE ASTRONOMER’S TRADE
Apparent Magnitude and Absolute Magnitude
Astronomers commonly express a star’s apparent brightness in terms of apparent magnitude (denoted by a lowercase m), and the star’s luminosity in terms of absolute magnitude (denoted by a capital M). While we do not use these quantities extensively in this book, it is useful to know a few simple relationships involving them.
Consider two stars, labeled 1 and 2, with apparent magnitudes m1 and m2 and brightnesses b1 and b2, respectively. The ratio of their apparent brightnesses (b1/b2) corresponds to a difference in their apparent magnitudes (m2 − m1). As we learned in Section 17-3, each step in magnitude corresponds to a factor of 2.512 in brightness; we receive 2.512 times more energy per square meter per second from a third-magnitude star than from a fourth-magnitude star. This idea was used to construct the following table:
| Apparent magnitude difference (m2 − m1) | Ratio of apparent brightness (b1/b2) |
|---|---|
| 1 | 2.512 |
| 2 | (2.512)2 = 6.31 |
| 3 | (2.512)3 = 15.85 |
| 4 | (2.512)4 = 39.82 |
| 5 | (2.512)5 = 100 |
| 10 | (2.512)10 = 104 |
| 15 | (2.512)15 = 106 |
| 20 | (2.512)20 = 108 |
A simple equation relates the difference between two stars’ apparent magnitudes to the ratio of their brightnesses:
Magnitude difference related to brightness ratio
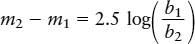
- m1, m2 = apparent magnitudes of stars 1 and 2
- b1, b2 = apparent brightnesses of stars 1 and 2
In this equation, log (b1/b2) is the logarithm of the brightness ratio. The logarithm of 1000 = 103 is 3, the logarithm of 10 = 101 is 1, and the logarithm of 1 = 100 is 0.
EXAMPLE: At their most brilliant, Venus has a magnitude of about −4 and Mercury has a magnitude of about −2. How many times brighter are these planets than the dimmest stars visible to the naked eye, with a magnitude of +6?
Situation: In each case we want to find a ratio of two apparent brightnesses (the brightness of Venus or Mercury compared to that of the dimmest naked-eye stars).
Tools: In each case we will convert a difference in apparent magnitude between the planet and the naked-eye star into a ratio of their brightnesses.
Answer: The magnitude difference between Venus and the dimmest stars visible to the naked eye is +6 − (−4) = 10. From the table, this difference corresponds to a brightness ratio of (2.512)10 = 104 = 10,000, so Venus at its most brilliant is 10,000 times brighter than the dimmest naked-eye stars.
The magnitude difference between Mercury and the dimmest naked-eye stars is +4 −(−4) = 8. While this value is not in the table, you can see that the corresponding ratio of brightnesses is (2.512)8 = (2.512)5+3 = (2.512)5 × (2.512)3. From the table, (2.512)5 = 100 and (2.512)3 = 15.85, so the ratio of brightnesses is 100 × 15.85 = 1585. Hence, Mercury at its most brilliant is 1585 times brighter than the dimmest stars visible to the naked eye.
Review: Can you show that when at their most brilliant, Venus is 6.31 times brighter than Mercury? (Hint: No multiplication or division is required—just notice the difference in apparent magnitude between Venus and Mercury, and consult the table.)
EXAMPLE: The variable star RR Lyrae in the constellation Lyra (the Harp) periodically doubles its light output. By how much does its apparent magnitude change?
Situation: We are given a ratio of two brightnesses (the star at its maximum is twice as bright as at its minimum). Our goal is to find the corresponding difference in apparent magnitude.
Tools: We let 1 denote the star at its maximum brightness and 2 denote the same star at its dimmest, so the ratio of brightnesses is b1/b2 = 2. We then use the equation m2 − m1 = 2.5 log (b1/b2) to solve for the apparent magnitude difference m2 − m1.
Answer: Using a calculator, we find m2 − m1 = 2.5 log (2) = 2.5 × 0.30 = 0.75. RR Lyrae therefore varies periodically in brightness by 0.75 magnitude.
Review: Our answer means that at its dimmest, RR Lyrae has an apparent magnitude m2 that is 0.75 greater than its apparent magnitude m1 when it is brightest. (Remember that a greater value of apparent magnitude means the star is dimmer, not brighter!)
The inverse-square law relating a star’s apparent brightness and luminosity can be rewritten in terms of the star’s apparent magnitude (m), absolute magnitude (M), and distance from Earth (d). This can be expressed as an equation:
476
Relation between a star’s apparent magnitude and absolute magnitude
m − M = 5 log d − 5
- m = star’s apparent magnitude
- M = star’s absolute magnitude
- d = distance from Earth to the star in parsecs
In this expression m − M is called the distance modulus, and log d means the logarithm of the distance d in parsecs. For convenience, the following table gives the values of the distance d corresponding to different values of m − M.
| Distance modulus m − M | Distance d (pc) |
|---|---|
| −4 | 1.6 |
| −3 | 2.5 |
| −2 | 4.0 |
| −1 | 6.3 |
| 0 | 10 |
| 1 | 16 |
| 2 | 25 |
| 3 | 40 |
| 4 | 63 |
| 5 | 100 |
| 10 | 103 |
| 15 | 104 |
| 20 | 105 |
This table shows that if a star is less than 10 pc away, its distance modulus m − M is negative. That is, its apparent magnitude (m) is less than its absolute magnitude (M). If the star is more than 10 pc away, m − M is positive and m is greater than M. As an example, the star ε (epsilon) Indi, which is in the direction of the southern constellation Indus, has apparent magnitude m = 14.7. It is 3.6 pc away, which is less than 10 pc, so its apparent magnitude is less than its absolute magnitude.
EXAMPLE: Find the absolute magnitude of ε Indi.
Situation: We are given the distance to ε Indi (d = 3.6 pc) and its apparent magnitude (m = 14.7). Our goal is to find the star’s absolute magnitude M.
Tools: We use the formula m − M = 5 log d − 5 to solve for M.
Answer: Since d = 3.6 pc, we use a calculator to find log d = log 3.6 = 0.56. Therefore the star’s distance modulus is m − M = 5(0.56) − 5 = −2.2, and the star’s absolute magnitude is M = m − (−2.2) = +4.7 + 2.2 = +6.9.
Review: As a check on our calculations, note that this star’s distance modulus m − M = − 2.2 is less than zero, as it should be for a star less than 10 pc away. Note that our Sun has absolute magnitude +4.8; ε Indi has a greater absolute magnitude, so it is less luminous than the Sun.
EXAMPLE: Suppose you were viewing the Sun from a planet orbiting another star 100 pc away. Could you see it without using a telescope?
Situation: We learned in the preceding examples that the Sun has absolute magnitude M = +4.8 and that the dimmest stars visible to the naked eye have apparent magnitude m = +6. Our goal is to determine whether the Sun would be visible to the naked eye at a distance of 100 pc.
Tools: We use the relationship m − M = 5 log d − 5 to find the Sun’s apparent magnitude at d = 100 pc. If this is greater than +6, the Sun would not be visible at that distance. (Remember that the greater the apparent magnitude, the dimmer the star.)
Answer: From the table, at d = 100 pc the distance modulus is m − M = 5. So, as seen from this distant planet, the Sun’s apparent magnitude would be m = M + 5 = +4.8 + 5 = +9.8. This is greater than the naked-eye limit m = +6, so the Sun could not be seen.
Review: The Sun is by far the brightest object in Earth’s sky. But our result tells us that to an inhabitant of a planetary system 100 pc away—a rather small distance in a galaxy that is thousands of parsecs across—our own Sun would be just another insignificant star, visible only through binoculars or a telescope.
The magnitude system is also used by astronomers to express the colors of stars as seen through different filters, as we describe in Section 17-4. For example, rather than quantifying a star’s color by the color ratio bV/bB (a star’s apparent brightness as seen through a V filter divided by the brightness through a B filter), astronomers commonly use the color index B–V, which is the difference in the star’s apparent magnitude as measured with these two filters. We will not use this system in this book, however (but see Advanced Questions 53 and 54).