TOOLS OF THE ASTRONOMER’S TRADE

You can estimate the angular sizes of objects in the sky with your hand and fingers (see Figure 1-12). Using rather more sophisticated equipment, astronomers can measure angular sizes to a fraction of an arcsecond. Keep in mind, however, that angular size is not the same as actual size. As an example, if you extend your arm while looking at a full moon, you can completely cover the Moon with your thumb. That’s because from your perspective, your thumb has a larger angular size (that is, it subtends a larger angle) than the Moon. But the actual size of your thumb (about 2 centimeters) is much less than the actual diameter of the Moon (more than 3000 kilometers).

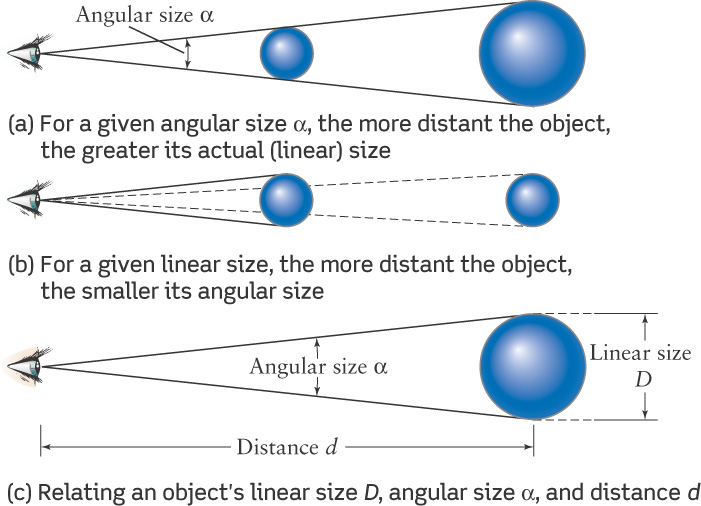
The accompanying figure shows how the angular size of an object is related to its linear size. Part (a) of the figure shows that for a given angular size, the more distant the object, the larger its actual size. For example, your fingertip held at arm’s length covers the full moon, but the Moon is much farther away and is far larger in linear size. Part (b) shows that for a given linear size, the angular size decreases the farther away the object. This is why a car looks smaller and smaller as it drives away from you.

We can put these relationships together into a single mathematical expression called the small-angle formula. Suppose that an object subtends an angle a (the Greek letter alpha) and is at a distance d from the observer, as in part (c) of the figure. If the angle a is small, as is almost always the case for objects in the sky, the width or linear size (D) of the object is given by the following expression:

The small-angle formula

(a) Two objects that have the same angular size may have different linear sizes if they are at different distances from the observer. (b) For an object of a given linear size, the angular size is smaller the farther the object is from the observer. (c) The small-angle formula relates the linear size D of an object to its angular size a and its distance d from the observer.

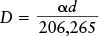
The number 206,265 is required in the formula so that the units of α are in arcseconds. (206,265 is the number of arcseconds in a complete 360° circle divided by the number 2π.) As long as the same units are used for D and d, any units for linear distance can be used (km, light-years, etc.).

The following examples show two different ways to use the small-angle formula. In both examples we follow a four-step process: Evaluate the situation given in the example, decide which tools are needed to solve the problem, use those tools to find the answer to the problem, and review the result to see what it tells you. Throughout this book, we’ll use these same four steps in all examples that require the use of formulas. We encourage you to follow this four-step process when solving problems for homework or exams. You can remember these steps by their acronym: S.T.A.R.

EXAMPLE: On December 11, 2006, Jupiter was 944 million kilometers from Earth and had an angular diameter of 31.2 arcsec. From this information, calculate the actual diameter of Jupiter in kilometers.

Situation: The astronomical object in this example is Jupiter, and we are given its distance d and its angular size π (the same as angular diameter). Our goal is to find Jupiter’s diameter D.

Tools: The equation to use is the small-angle formula, which relates the quantities d, α, and D. Note that when using this formula, the angular size α must be expressed in arcseconds.

Answer: The small-angle formula as given is an equation for D. Plugging in the given values α = 31.2 arcsec and d = 944 million kilometers,

Because the distance d to Jupiter is given in kilometers, the diameter D is also in kilometers.

Review: Does our answer make sense? From Appendix 2 at the back of this book, the equatorial diameter of Jupiter measured by spacecraft flybys is 142,984 kilometers, so our calculated answer is very close.

EXAMPLE: Under excellent conditions, a telescope on Earth can see details with an angular size as small as 1 arcsec. What is the greatest distance at which you could see details as small as 1.7 meters (the height of a typical person) under these conditions?

Situation: Now the object in question is a person, whose linear size D we are given. Our goal is to find the distance d at which the person has an angular size α equal to 1 arcsec.

Tools: Again we use the small-angle formula to relate d, α, and D.

Answer: We first rewrite the formula to solve for the distance d, then plug in the given values D = 1.7 m and α = 1 arcsec:

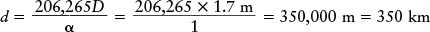
Review: This value is much less than the distance to the Moon, which is 384,000 kilometers. Thus, even the best telescope on Earth could not be used to see an astronaut walking on the surface of the Moon.