4-7 Describing orbits with energy and gravity
 Imagine a cannonball shot into the air; it arcs through the sky before it crashes back to the ground. If you want to shoot the cannonball into orbit around Earth (like a satellite), you might guess that the ball must be shot faster to give it more energy. This guess is correct, and next we’ll look at how to understand orbits in terms of gravity and energy.
Imagine a cannonball shot into the air; it arcs through the sky before it crashes back to the ground. If you want to shoot the cannonball into orbit around Earth (like a satellite), you might guess that the ball must be shot faster to give it more energy. This guess is correct, and next we’ll look at how to understand orbits in terms of gravity and energy.
90
Different Forms of Energy
Energy comes in a variety of familiar forms. For example, consider a car: The faster a car moves, the greater its energy. In general, the greater an object’s speed, the more kinetic energy it has (Figure 4-20). The word kinetic refers to motion, so kinetic energy is the energy of motion. However, the mass of an object also contributes to its kinetic energy, and a speeding car therefore has more kinetic energy than a speeding bullet.

Now let’s look at some other forms of energy. Both food and batteries store chemical energy, although they each contain very different chemicals. When energy is stored, we say it has the potential to be used, and this stored energy is often called potential energy. Consider a girl on the diving board of a swimming pool (Figure 4-21); gravity has the potential to pull her into the water (whenever she steps off the board). This is an example of stored gravitational energy, or gravitational potential energy. The higher the diving board, the more gravitational potential energy she has. After she steps off the board, she’ll have both kinetic energy and gravitational potential energy. As she falls towards the water, her kinetic energy increases and her gravitational potential energy decreases.

While the concept of energy is easier to introduce with a diving board, the same principles apply to orbiting objects: Planets, moons, and satellites also have both kinetic and gravitational potential energy. For example, the faster a satellite orbits Earth, the greater its kinetic energy, and if it falls back to Earth, it loses gravitational potential energy.
To understand another aspect of energy, let’s think more about the diver in Figure 4-21. Standing high atop the board, the diver has more gravitational potential energy than she would have while standing on the ground. In midair during the dive, some of that gravitational potential energy has transformed into kinetic energy. This illustrates a law called the conservation of energy: While energy can change from one form to another, energy cannot be created or destroyed.
There’s another way to express the law of conservation of energy. First consider a collection of objects that are isolated, which means no energy can leave or enter this collection of objects. Second, find the total energy by taking into account all the forms of energy the collection of objects has. This total energy is conserved, meaning that the total energy stays constant over time, even as objects interact with each other and the various forms of energy can change.
As a feather falls gently to the ground it loses gravitational potential energy without gaining much kinetic energy. This is an example of air drag, where the kinetic energy of an object is transferred to the molecules in the surrounding air and the air gets hotter. Energy is still conserved—as it always is—and the nearby air molecules actually speed up. Since the kinetic energy of individual particles gives a gas its temperature and thermal energy, we can see that air drag converts kinetic energy into thermal energy (we will learn more about thermal energy in Section 5-3). Air drag can be good or bad, depending on the situation. Astronauts returning to Earth rely on this transfer of energy, as they use air drag during atmospheric reentry to reduce their speed for a safe landing. As we will see shortly, air drag is undesirable when it transfers energy away from an orbiting satellite, causing it to fall back to Earth.
CONCEPT CHECK 4-19
Consider a cannonball shot vertically, straight up into the air. At the ball’s highest point, it momentarily comes to a complete stop before beginning to fall back down. At its highest point, what form of energy does the ball have, and where did the energy come from?
Gravitational Force, Energy, and Orbits
Because there is a gravitational force between any two objects, Newton concluded that gravity is also the force that keeps the Moon in orbit around Earth. It is also the force that keeps artificial satellites in orbit. But if the force of gravity attracts two objects to each other, why don’t satellites immediately fall to Earth? Why doesn’t the Moon fall into Earth? And, for that matter, why don’t the planets fall into the Sun?
91
To see the answer, imagine (as Newton did) dropping a ball from a great height above Earth’s surface, as in Figure 4-22. After you drop the ball, it, of course, falls straight down (path A in Figure 4-22). But if you throw the ball horizontally, it travels some distance across Earth’s surface before hitting the ground (path B). If you throw the ball harder, it travels a greater distance (path C). If you could throw or shoot it at just the right speed, the curvature of the ball’s path will exactly match the curvature of Earth’s surface (path E). Although Earth’s gravity is making the ball fall, Earth’s surface is falling away under the ball at the same rate. Hence, the ball does not get any closer to the surface, and the ball is in circular orbit. So, the ball in path E is in fact falling, but it is falling around Earth rather than toward Earth.
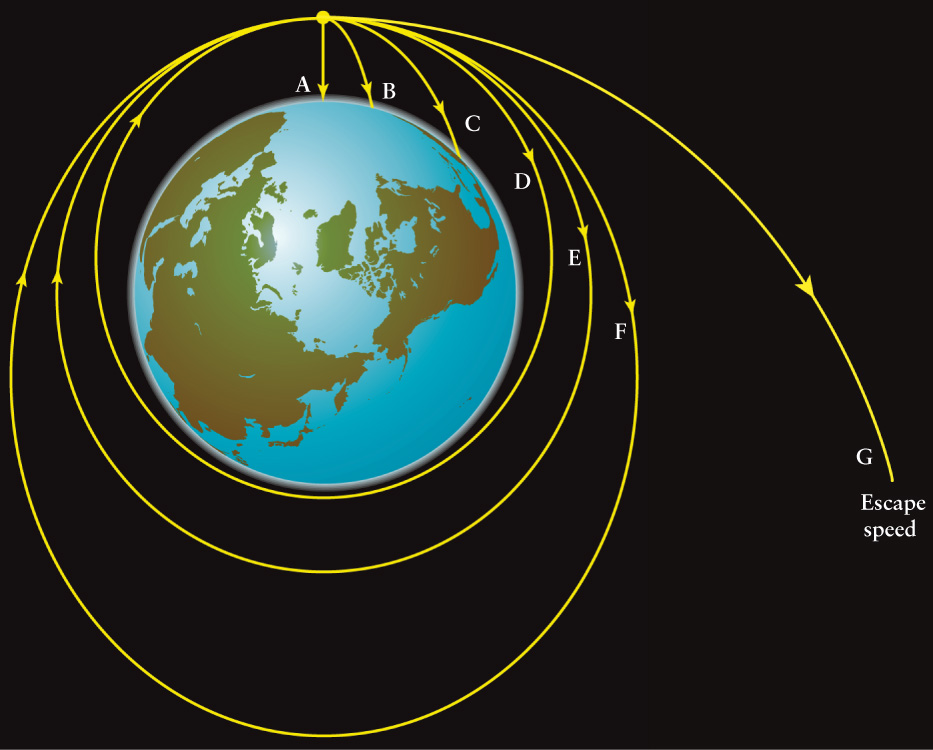
 Orbits and the Escape Speed If a ball is dropped from a great height above Earth’s surface, it falls straight down (A). If the ball is thrown with some horizontal speed, it follows a curved path before hitting the ground (B, C). If thrown with just the right speed (E), the ball goes into circular orbit; the ball’s path curves but it never gets any closer to Earth’s surface. If the ball is thrown with a speed that is slightly less (D) or slightly more (F) than the speed for a circular orbit, the ball’s orbit is an ellipse. If thrown faster than the escape speed (G), the ball will leave Earth and never return.
Orbits and the Escape Speed If a ball is dropped from a great height above Earth’s surface, it falls straight down (A). If the ball is thrown with some horizontal speed, it follows a curved path before hitting the ground (B, C). If thrown with just the right speed (E), the ball goes into circular orbit; the ball’s path curves but it never gets any closer to Earth’s surface. If the ball is thrown with a speed that is slightly less (D) or slightly more (F) than the speed for a circular orbit, the ball’s orbit is an ellipse. If thrown faster than the escape speed (G), the ball will leave Earth and never return.
As the hypothetical ball is launched faster and faster, you can also see that the paths (going from A to F) represent trajectories with more of both kinetic and gravitational potential energy; in other words, with increasing orbital energy. In general for an object orbiting the Sun or a planet:
The greater the orbital energy, the greater the average orbital distance (or the greater the semimajor axis, a).
A spacecraft is launched into orbit in just this way—by gaining enough speed and energy. Once the spacecraft is in orbit, no more rocket fuel is needed and, if not for air drag, the spacecraft could orbit indefinitely. However, air drag from the thin outer wisps of Earth’s atmosphere slowly removes orbital energy from the closer satellites, slowing them down, and bringing them inward. Without occasional bursts of thrust, these satellites would fall back to Earth. The International Space Station is no exception, and air drag can decrease the station’s altitude by a couple hundred feet each day!
CAUTION!
An astronaut on board an orbiting spacecraft (like the one shown in the photograph that opens this chapter) feels “weightless”. However, this is not because she is “beyond the pull of gravity”. The astronaut is herself an independent satellite of Earth, and Earth’s gravitational pull is what holds her in orbit. She feels “weightless” because she and her spacecraft are falling together around Earth, so there is nothing pushing her against any of the spacecraft walls. You feel the same “weightless” sensation whenever you are falling, such as when you jump off a diving board or ride the free-fall ride at an amusement park.
92
CONCEPT CHECK 4-20
Suppose a spacecraft is initially shot into a circular orbit with path E in Figure 4-22. Which new path will the spacecraft likely take if air drag is present? Which new path will likely result if a rocket thruster is fired?
CONCEPT CHECK 4-21
As Earth orbits the Sun, does Earth’s orbit decay due to air drag from its own atmosphere?
The Escape Speed
If an object is hurled with enough speed, it can escape a planet altogether. For example, when a very large asteroid smashes into Earth, most of the debris ejected from the crater falls back to Earth’s surface, but some rocks have enough speed to escape and roam the solar system. In Figure 4-22, the object on path G is shot with the escape speed, has more energy than any of the “bound” orbits, and never returns to Earth’s orbit. The speed needed for escape depends on the size and mass of the planet, but not on the mass of the escaping object:
Escape Speed

For Earth, the escape speed is 11.2 km/s. That’s about 25,000 mi/h, or 33 times the speed of sound. This speed is so fast that, except for the largest asteroid impacts, very little debris would have escaped Earth. However, the escape speed for Mars is only about 5 km/s, so compared to Earth, it is easier for impact debris from Mars to get ejected into the solar system. (In fact, about 100 rocks found on Earth were originally ejected from Mars by asteroid impacts.)
What about spacecraft; are they launched at the escape speed? The escape speed assumes a simple scenario where no air drag is present and where there is no rocket fuel to add energy during flight. However, even with fuel, spacecraft going to the Moon or beyond often leave Earth near the escape speed.
CONCEPT CHECK 4-22
Two objects, a large rock and a small rock, are shot with just enough speed to escape the Moon. Can both rocks be shot with equal speed? Can both rocks be shot with the same kinetic energy?
CONCEPT CHECK 4-23
New planets around other stars are constantly being discovered. Would it be possible to find a planet with the same mass as Earth but with a lower escape speed from its surface?
Gravitation and Kepler’s Laws
Using his three laws of motion and his law of gravity, Newton found that he could derive Kepler’s three laws mathematically. (Newton also invented calculus, which helped in this endeavor!) While Kepler’s laws describe the planets in the solar system specifically, Newton showed that similar behavior results from any orbital system, such as a planet and its moons. Kepler’s first law, concerning the elliptical shape of planetary orbits, proved to be a direct consequence of the 1/r2 factor in the law of universal gravitation. The law of equal areas, or Kepler’s second law, turns out to be a consequence of the Sun’s gravitational force on a planet being directed straight toward the Sun.
93
Newton also demonstrated that Kepler’s third law follows logically from his law of gravity. Specifically, he proved that if two objects with masses m1 and m2 orbit each other, the period P of their orbit and the semimajor axis a of their orbit (that is, the average distance between the two objects) are related by an equation that we call Newton’s form of Kepler’s third law:
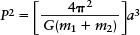
Newton’s form of Kepler’s third law is valid whenever two objects orbit each other because of their mutual gravitational attraction (Figure 4-23). It is invaluable in the study of binary star systems, in which two stars orbit each other. If the orbital period P and semimajor axis a of the two stars in a binary system are known, astronomers can use this formula to calculate the sum m1 + m2 of the masses of the two stars. Within our own solar system, Newton’s form of Kepler’s third law makes it possible to learn about the masses of planets. By measuring the period and semimajor axis for a satellite, astronomers can determine the sum of the masses of the planet and the satellite. (The satellite can be a moon of the planet or a spacecraft that we place in orbit around the planet. Newton’s laws apply in either case.) Box 4-4 gives an example of using Newton’s form of Kepler’s third law.

In Orbit Around the Moon This photograph taken from the spacecraft Columbia shows the lunar lander Eagle after returning from the first human landing on the Moon in July 1969. Newton’s form of Kepler’s third law describes the orbit of a spacecraft around the Moon, as well as the orbit of the Moon around Earth (visible in the distance).
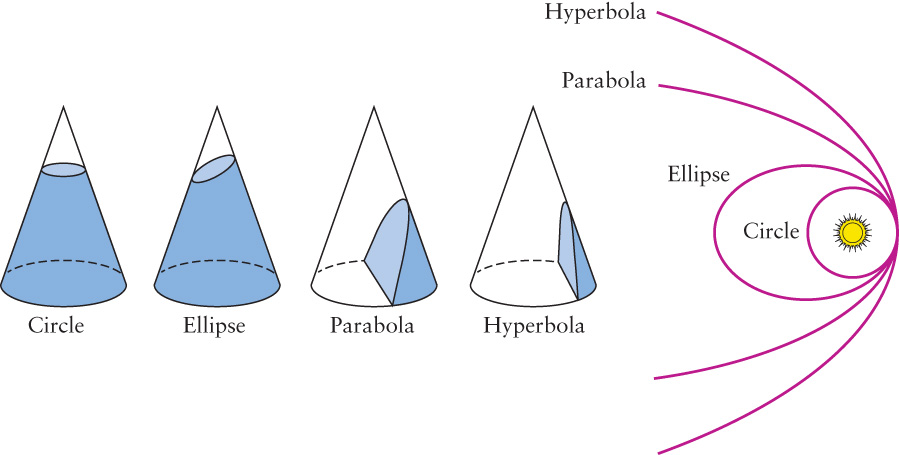
Newton also discovered new features of orbits around the Sun. For example, his equations soon led him to conclude that the orbit of an object around the Sun need not be an ellipse. It could be any one of a family of curves called conic sections.
TOOLS OF THE ASTRONOMER’S TRADE
Newton’s Form of Kepler’s Third Law
Kepler’s original statement of his third law, P2 = a3, is valid only for objects that orbit the Sun. (Box 4-2 shows how to use this equation.) But Newton’s form of Kepler’s third law is much more general: It can be used in any situation where two objects of masses m1 and m2 orbit each other. For example, Newton’s form is the equation to use for a moon orbiting a planet or a satellite orbiting Earth. This equation is
Newton’s form of Kepler’s third law:

Notice that P, a, m1, and m2 must be expressed in these particular units. If you fail to use the correct units, your answer will be incorrect.
EXAMPLE: Io (pronounced “eye-oh”) is one of the four large moons of Jupiter discovered by Galileo and shown in Figure 4-16. It orbits at a distance of 421,600 km from the center of Jupiter and has an orbital period of 1.77 days. Determine the combined mass of Jupiter and Io.
Situation: We are given Io’s orbital period P and semimajor axis a (the distance from Io to the center of its circular orbit, which is at the center of Jupiter). Our goal is to find the sum of the masses of Jupiter (m1) and Io (m2).
Tools: Because this orbit is not around the Sun, we must use Newton’s form of Kepler’s third law to relate P and a. This relationship also involves m1 and m2, whose sum (m1 + m2) we are asked to find.
Answer: To solve for m1 + m2, we rewrite the equation in the form
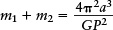
To use this equation, we have to convert the distance a from kilometers to meters and convert the period P from days to seconds. There are 1000 meters in 1 kilometer and 86,400 seconds in 1 day, so

We can now put these values and the value of G into the above equation:

Review: Io is very much smaller than Jupiter, so its mass is only a small fraction of the mass of Jupiter. Thus, m1 + m2 is very nearly the mass of Jupiter alone. We conclude that Jupiter has a mass of 1.90 × 1027 kg, or about 300 times the mass of Earth. This technique can be used to determine the mass of any object that has a second, much smaller object orbiting it. Astronomers use this technique to find the masses of stars, black holes, and entire galaxies of stars.
94
A conic section is any curve that you get by cutting a cone with a plane, as shown in Figure 4-24. You can get circles and ellipses by slicing all the way through the cone, and these represent the familiar circular and elliptical orbits. You can also get two types of open curves called parabolas and hyperbolas. An object traveling at the escape speed follows a parabolic curve, and for objects traveling even faster than the escape speed, the path is hyperbolic. Comets hurtling toward the Sun from the depths of space sometimes follow hyperbolic orbits and never return.
CONCEPT CHECK 4-24
A small celestial object on a hyperbolic orbit passes by a lonely moonless planet. Can the planet capture the object to acquire a moon?
The Triumph of Newtonian Mechanics
Newton’s ideas turned out to be applicable to an incredibly wide range of situations. Using his laws of motion, Newton himself proved that Earth’s axis of rotation must precess because of the gravitational pull of the Moon and the Sun on Earth’s equatorial bulge (see Figure 2-19). In fact, all the details of the orbits of the planets and their satellites could be explained mathematically with a body of knowledge built on Newton’s work that is today called Newtonian mechanics.
Not only could Newtonian mechanics explain a variety of known phenomena in detail, but it could also predict new phenomena. For example, one of Newton’s friends, Edmund Halley, was intrigued by three similar historical records of a comet that had been sighted at intervals of 76 years. Assuming these records to be accounts of the same comet, Halley used Newton’s methods to work out the details of the comet’s orbit and predicted its return in 1758. It was first sighted on Christmas night of 1757, a fitting memorial to Newton’s birthday. To this day the comet bears Halley’s name (Figure 4-25).

Comet Halley This most famous of all comets orbits the Sun with an average period of about 76 years. During the twentieth century, the comet passed near the Sun in 1910 and again in 1986 (when this photograph was taken). It will next be prominent in the sky in 2061.
Another dramatic success of Newton’s ideas was their role in the discovery of the eighth planet from the Sun. The seventh planet, Uranus, was discovered accidentally by William Herschel in 1781 during a telescopic survey of the sky. Fifty years later, however, it was clear that Uranus was not following its predicted orbit. John Couch Adams in England and Urbain Le Verrier in France independently calculated that the gravitational pull of a yet unknown, more distant planet could explain the deviations of Uranus from its orbit. Le Verrier predicted that the planet would be found at a certain location in the constellation of Aquarius. A brief telescopic search on September 23, 1846, revealed the planet Neptune within 1° of the calculated position. Before it was sighted with a telescope, Neptune was actually predicted with pencil and paper.
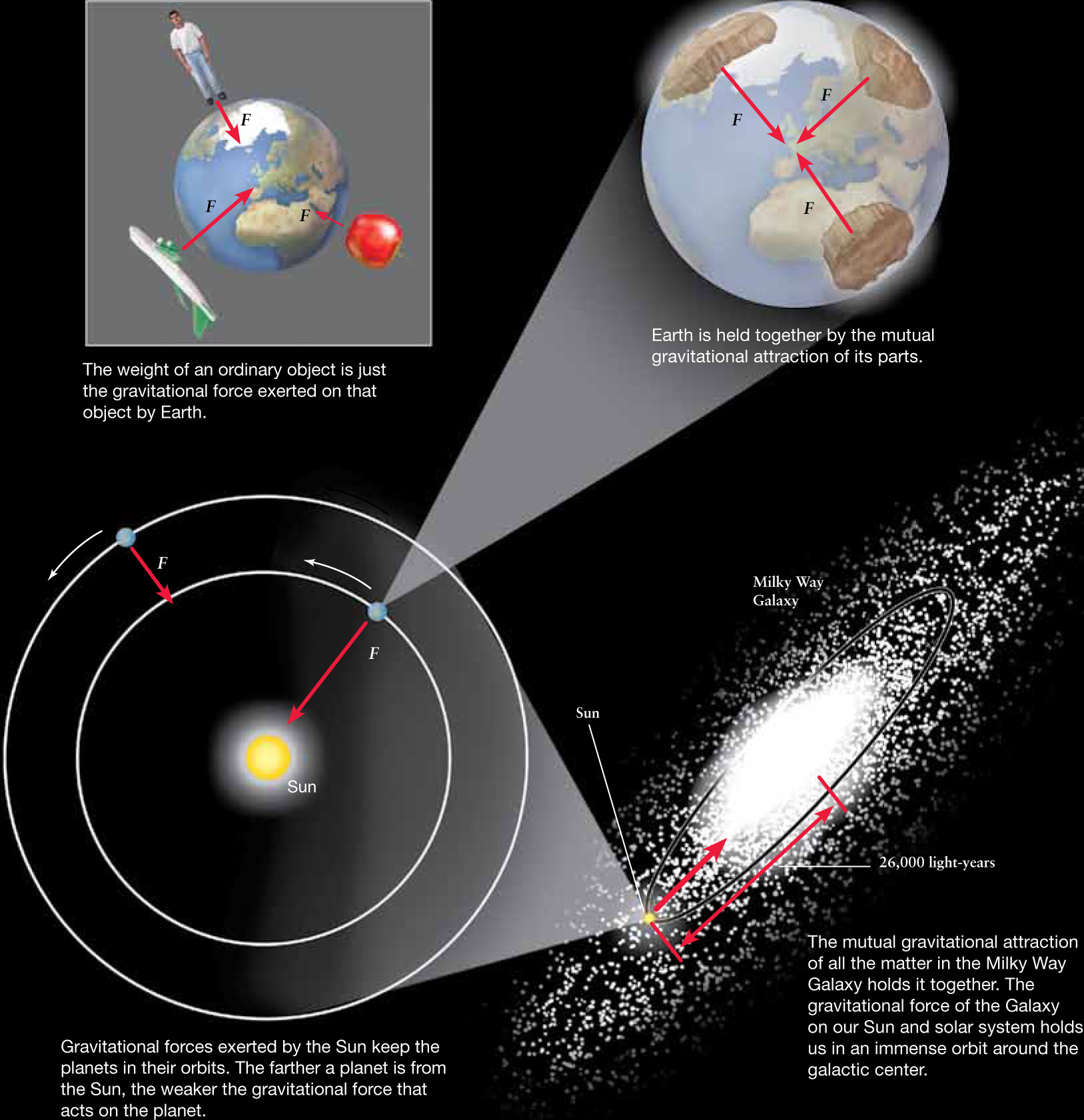
Because it has been so successful in explaining and predicting many important phenomena, Newtonian mechanics has become the cornerstone of modern physical science. Even today, as we send astronauts into Earth orbit and spacecraft to the outer planets, Newton’s equations are used to calculate the orbits and trajectories of these spacecraft. The Cosmic Connections figure summarizes some of the ways that gravity plays an important role on scales from apples to galaxies.
95
COSMIC CONNECTIONS
Universal Gravitation
Gravity is one of the fundamental forces of nature. We can see its effects here on Earth as well as in the farthest regions of the observable universe.
96
In the twentieth century, scientists found that Newton’s laws do not apply in all situations. A new theory called quantum mechanics had to be developed to explain the behavior of matter on the very smallest of scales, such as within the atom and within the atomic nucleus. Albert Einstein developed the theory of relativity to explain what happens at very high speeds approaching the speed of light and in places where gravitational forces are very strong. For many purposes in astronomy, however, Newton’s laws are as useful today as when Newton formulated them more than three centuries ago.