Question 1 of 3

Country A and country B both have the production function

Y = F(K, L) = K^1/2L^1/2.

Does this production function have constant returns to scale?

What is the per‑worker production function, y = f(k)?

Country A and country B both have the production function

Y = F(K, L) = K^1/2L^1/2.

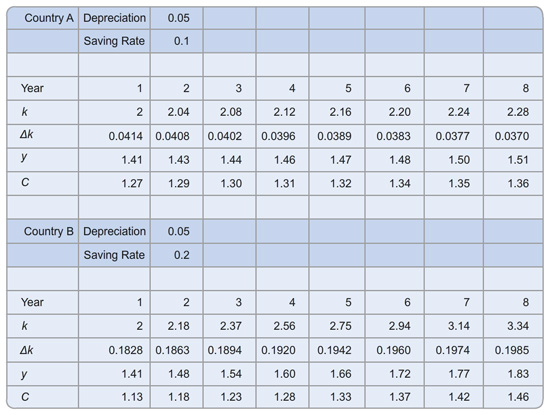
Assume that neither country experiences population growth or technological progress and that 5 percent of capital depreciates each year. Assume further that country A saves 10 percent of output each year and country B saves 20 percent of output each year. Using your answer from part (b) and the steady-state condition that investment equals depreciation, find the steady-state level of capital per worker for each country. Then find the steady-state levels of income per worker and consumption per worker.

Country A:

k* =

y* =

c* =

Country B:

k* =

y* =

c* =

Country A and country B both have the production function

Y = F(K, L) = K^1/2L^1/2.

Suppose that both countries start off with a capital stock per worker of 2. What are the levels of income per worker and consumption per worker? Round your answers to two decimal places.

Country A:

y =

c =

Country B:

y =

c =

Review text pages 212-219 and Table 8-2 for a discussion of capital accumulation in the Solow growth model and details of how the economy adjusts to its steady state.

Review text pages 212-219 and Table 8-2 for a discussion of capital accumulation in the Solow growth model and details of how the economy adjusts to its steady state.