335

9

A Logician’s View: Deduction, Induction, Fallacies

Logic is the anatomy of thought.

— JOHN LOCKE

Logic takes care of itself; all we have to do is to look and see how it does it.

— LUDWIG WITTGENSTEIN

In Chapter 3 we introduced the terms deduction, induction, and fallacy. Here we discuss them in greater detail.

Deduction

The basic aim of deductive reasoning is to start with some assumption or premise and extract from it a conclusion — a logical consequence — that is concealed but implicit in it. Thus, taking the simplest case, if I assert as a premise

1a. Nuclear power poses more risks of harm to the environment than fossil fuels.

then it is a matter of simple deduction to infer the conclusion that

1b. Fossil fuels pose fewer risks of harm to the environment than nuclear power.

Anyone who understands English would grant that 1b follows 1a — or equivalently, that 1b can be validly deduced from 1a — because whatever two objects, A and B, you choose, if A does more things than B, then B must do fewer things than A.

Thus, in this and all other cases of valid deductive reasoning, we can say not only that we are entitled to infer the conclusion from the premise — in this case, infer 1b from 1a — but that the premise implies the conclusion. Remember, too, the conclusion (1b) that fossil fuels pose fewer risks than nuclear power — inferred or deduced from the statement (1a) that nuclear power poses more risks — does not depend on the truth of the statement that nuclear power poses more risks. If the speaker (falsely) asserts that nuclear power poses more risks, then the hearer validly (i.e., logically) concludes that fossil fuels pose fewer risks. Thus, 1b follows from 1a whether or not 1a is true; consequently, if 1a is true, then so is 1b; but if 1a is false, then 1b must be false also.

336

Let’s take another example — more interesting but comparably simple:

2a. President Truman was underrated by his critics.

Given 2a, a claim amply verified by events of the 1950s, one is entitled to infer that

2b. His critics underrated President Truman.

On what basis can we argue that 2a implies 2b? The two propositions are equivalent because a rule of English grammar assures us that we can convert the position of subject and predicate phrases in a sentence by shifting from the passive to the active voice (or vice versa) without any change in the conditions that make the proposition true (or false).

Both pairs of examples illustrate that in deductive reasoning, our aim is to transform, reformulate, or restate in our conclusion some (or, as in the two examples above, all) of the information contained in our premises.

Remember, even though a proposition or statement follows from a previous proposition or statement, the statements need not be true. We can see why if we consider another example. Suppose someone asserts or claims that

3a. The Gettysburg Address is longer than the Declaration of Independence.

As every student of American history knows, 3a is false. But false or not, we can validly deduce from it that

3b. The Declaration of Independence is shorter than the Gettysburg Address.

This inference is valid (even though the conclusion is untrue) because the conclusion follows logically (more precisely, deductively) from 3a: In English, as we know, the meaning of “A is shorter than B,” which appears in 3b, is simply the converse of “B is longer than A,” which appears in 3a.

The deductive relation between 3a and 3b reminds us again that the idea of validity, which is so crucial to deduction, is not the same as the idea of truth. False propositions have implications — logical consequences — too, just as true propositions do.

In the three pairs of examples so far, what can we point to as the warrant for our claims? Well, look at the reasoning in each case; the arguments rely on rules of ordinary English, on the accepted meanings of words like on, under, and underrated.

In many cases, of course, the deductive inference or pattern of reasoning is much more complex than that which we have seen in the examples so far. When we introduced the idea of deduction in Chapter 3, we gave as our primary example the syllogism. Here is another example:

4. Texas is larger than California; California is larger than Arizona; therefore, Texas is larger than Arizona.

337

The conclusion in this syllogism can be derived from the two premises; that is, anyone who asserts the two premises is committed to accepting the conclusion as well, whether or not one thinks of it.

Notice again that the truth of the conclusion is not established merely by validity of the inference. The conclusion in this syllogism happens to be true. And the premises of this syllogism imply the conclusion. But the argument establishes the conclusion only because both of the premises on which the conclusion depends are true. Even a Californian admits that Texas is larger than California, which in turn is larger than Arizona. In other words, argument 4 is a sound argument because (as we explained in Chapter 3) it is valid and all its premises are true. All — and only — arguments that prove their conclusions have these two traits.

How might we present the warrant for the argument in 4? Short of a crash course in formal logic, either of two strategies might suffice. One is to argue from the fact that the validity of the inference depends on the meaning of a key concept, being larger than. This concept has the property of transitivity, a property that many concepts share (e.g., is equal to, is to the right of, is smarter than — all are transitive concepts). Consequently, whatever A, B, and C are, if A is larger than B, and B is larger than C, then A will be larger than C. The final step is to substitute “Texas,” “California,” and “Arizona” for A, B, and C, respectively.

A second strategy, less abstract and more graphic, is to think of representing Texas, California, and Arizona by nested circles. Thus, the first premise in argument 4 would look like this:

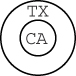
The second premise would look like this:

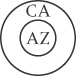
The conclusion would look like this:

We can see that this conclusion follows from the premises because it amounts to nothing more than what one gets by superimposing the two premises on each other. Thus, the whole argument can be represented like this:

338

The so-called middle term in the argument — California — disappears from the conclusion; its role is confined to be the link between the other two terms, Texas and Arizona, in the premises. (This is an adaptation of the technique used in elementary formal logic known as Venn diagrams.) In this manner one can give graphic display to the important fact that the conclusion follows from the premises because one can literally see the conclusion represented by nothing more than a representation of the premises.

Both of these strategies bring out the fact that validity of deductive inference is a purely formal property of argument. Each strategy abstracts the form from the content of the propositions involved to show how the concepts in the premises are related to the concepts in the conclusion.

For the sake of illustration, here is another syllogistic argument with the same logical features as argument 4. (A nice exercise is to restate argument 5 using diagrams in the manner of argument 4.)

5. African American slaves were treated worse than white indentured servants. Indentured white servants were treated worse than free white labor. Therefore, African American slaves were treated worse than free white labor.

Not all deductive reasoning occurs in syllogisms, however, or at least not in syllogisms like the ones in 4 and 5. (The term syllogism is sometimes used to refer to any deductive argument of any form, provided only that it has two premises.) In fact, syllogisms such as 4 are not the commonest form of our deductive reasoning at all. Nor are they the simplest (and, of course, not the most complex). For an argument that is even simpler, consider this:

6. If a youth is an African American slave, he is probably treated worse than a youth in indentured service. This youth is an African American slave. Therefore, he is probably treated worse than if he had been an indentured servant.

Here the pattern of reasoning has the form: If A, then B; A; therefore, B. Notice that the content of the assertions represented by A and B don’t matter; any set of expressions having the same form or structure will do equally well, including assertions built out of meaningless terms, as in this example:

7. If the slithy toves, then the gyres gimble. The slithy toves. Therefore, the gyres gimble.

Argument 7 has the form: If A, then B; A; therefore B. As a piece of deductive inference it is every bit as good as argument 6. Unlike 6, however, 7 is of no interest to us because none of its assertions make any sense (unless you’re a reader of Lewis Carroll’s “Jabberwocky,” and even then the sense of 7 is doubtful). You cannot, in short, use a valid deductive argument to prove anything unless the premises and the conclusion are true, but they can’t be true unless they mean something in the first place.

This parallel between arguments 6 and 7 shows once again that deductive validity in an argument rests on the form or structure of the argument, and not on its content or meaning. If all one can say about an argument is that it is valid — that is, its conclusion follows from the premises — one has not given a sufficient reason for accepting the argument’s conclusion. It has been said that the devil can quote scripture; similarly, an argument can be deductively valid and of no further interest or value whatever because valid (but false) conclusions can be drawn from false or even meaningless assumptions. For example:

339

8. New York’s Metropolitan Museum of Art has the finest collection of abstract impressionist paintings in the world. The finest collection of abstract impressionist paintings includes dozens of canvases by Winslow Homer. Therefore, the Metropolitan Museum of Art has dozens of paintings by Winslow Homer.

Here the conclusion follows validly from the premises, even though all three propositions are false. Nevertheless, although validity by itself is not enough, it is a necessary condition of any deductive argument that purports to establish its conclusion.

Now let’s consider another argument with the same form as 8, only more interesting:

9. If President Truman knew the Japanese were about to surrender, then it was immoral of him to order that atom bombs be dropped on Hiroshima and Nagasaki. Truman knew the Japanese were about to surrender. Therefore, it was immoral of him to order dropping those bombs.

As in the two previous examples, anyone who assents to the premises in argument 9 must assent to the conclusion; the form of arguments 8 and 9 is identical. But do the premises of argument 9 prove the conclusion? That depends on whether both premises are true. Well, are they? This turns on a number of considerations, and it is worthwhile pausing to examine this argument closely to illustrate the kinds of things that are involved in answering this question.

Let’s begin by examining the second (minor) premise. Its truth is controversial even to this day. Autobiography, memoranda, other documentary evidence — all are needed to assemble the evidence to back up the grounds for the thesis or claim made in the conclusion of this valid argument. Evaluating this material effectively will probably involve not only further deductions but inductive reasoning as well.

Now consider the first (major) premise in argument 9. Its truth doesn’t depend on what history shows but on the moral principles one accepts. The major premise has the form of a hypothetical proposition (“if . . . then . . .”) and asserts a connection between two very different kinds of things. The antecedent of the hypothetical (the clause following “if”) mentions facts about Truman’s knowledge, and the consequent of the hypothetical (the clause following “then”) mentions facts about the morality of his conduct in light of such knowledge. The major premise as a whole can thus be seen as expressing a principle of moral responsibility.

Such principles can, of course, be controversial. In this case, for instance, is the principle peculiarly relevant to the knowledge and conduct of a president of the United States? Probably not; it is far more likely that this principle is merely a special case of a more general proposition about anyone’s moral responsibility. (After all, we know a great deal more about the conditions of our own moral responsibility than we do about those of high government officials.) We might express this more general principle in this way: If we have knowledge that would make our violent conduct unnecessary, then we are immoral if we deliberately act violently anyway. Thus, accepting this general principle can serve as a basis for defending the major premise of argument 9.

340

We have examined this argument in some detail because it illustrates the kinds of considerations needed to test not only whether a given argument is valid but also whether its premises are true — that is, whether its premises really prove the conclusion.

The great value of the form of argument known as hypothetical syllogism, exemplified by arguments 6 and 7, is that the structure of the argument is so simple and so universally applicable in reasoning that it is often both easy and worthwhile to formulate one’s claims so that they can be grounded by an argument of this sort.

Before leaving the subject of deductive inference, let’s consider three other forms of argument, each of which can be found in actual use elsewhere in the readings in this volume. The simplest of these is disjunctive syllogism, so called because its major premise is a disjunction. For example:

10. Either censorship of television shows is overdue, or our society is indifferent to the education of its youth. Our society is not indifferent to the education of its youth. Therefore, censorship of television is overdue.

Notice, by the way, that the validity of an argument, as in this case, does not turn on pedantic repetition of every word or phrase as the argument moves along; nonessential elements can be dropped, or equivalent expressions substituted for variety without adverse effect on the reasoning. Thus, in conversation or in writing, the argument in 10 might actually be presented like this:

11. Either censorship of television is overdue, or our society is indifferent to the education of its youth. But, of course, we aren’t indifferent; it’s censorship that’s overdue.

The key feature of disjunctive syllogism, as example 11 suggests, is that the conclusion is whichever of the disjuncts is left over after the others have been negated in the minor premise. Thus, we could easily have a very complex disjunctive syllogism, with a dozen disjuncts in the major premise, and seven of them denied in the minor premise, leaving a conclusion of the remaining five. Usually, however, a disjunctive argument is formulated in this manner: Assert a disjunction with two or more disjuncts in the major premise; then deny all but one in the minor premise; and infer validly the remaining disjunct as the conclusion. That was the form of argument 11.

Another type of argument, especially favored by orators and rhetoricians, is the dilemma. Ordinarily, we use the term dilemma in the sense of an awkward predicament, as when we say, “His dilemma was that he didn’t have enough money to pay the waiter.” But when logicians refer to a dilemma, they mean a forced choice between two or more equally unattractive alternatives. For example, the predicament faced by the U.S. government in 2014 in deciding how to deal with the growth of the Islamic State in Syria can be posed as a dilemma. Two major choices emerged. The United States could ally itself with the Syrian government, or it could support rebel groups inside Syria who fight against ISIS. The dilemma is that the Syrian government, a dictatorship under Bashar al-Assad, has attempted to crush political reform movements in Syria, and it actively supports groups the United States deems terrorist organizations, such as Hamas and Hezbollah. Also, some important U.S. allies such as Saudi Arabia oppose the al-Assad regime. On the other hand, if the United States were to support resistance groups within Syria, it would open itself up to charges that it was funding and arming groups hostile to the al-Assad regime, making them vulnerable to attack from the Syrian government and angering Syrian allies such as Russia, which may well be called upon to support strikes against the United States. The dilemma might be phrased as such:

341

12. If the United States supports the Syrian government, it would also be supporting a dictatorship that has been linked to terrorism and crimes against humanity, and that furthermore is an enemy of some of our closest Middle Eastern allies. If the United States supports rebel groups within Syria, it may be subject to attack by the al-Assad regime, extending the Syrian civil war and inviting potentially dangerous conflict with Russia. Either the United States supports a dictatorship, or it supports internal resistance groups. In either case, unattractive consequences follow.

Notice first the structure of the argument: two conditional propositions asserted as premises, followed by another premise that states a necessary truth. (The premise, “Either we support the Libyan dictatorship, or we support the Libyan rebels,” is a disjunction; since its two alternatives are exhaustive, one of the two alternatives must be true. Such a statement is often called analytically true, or a tautology.) No doubt the conclusion of this dilemma follows from its premises.

But does the argument prove, as it purports to do, that whatever the U.S. government does, it will suffer “unattractive consequences”? It is customary to speak of “the horns of the dilemma,” as though the challenge posed by the dilemma were like a bull ready to gore us no matter which direction we turn. But if the two conditional premises failed to exhaust the possibilities, then we can escape from the dilemma by going “between the horns,” that is, by finding a third alternative. If (as in this case) that isn’t possible, we can still ask whether both of the main premises are true. (In this argument, it should be clear that neither of the main premises spells out all or even most of the consequences that could be foreseen.) Even so, in cases where both of these conditional premises are true, it may be that the consequences of one alternative are nowhere nearly so bad as those of the other. If that is true, but our reasoning stops before evaluating that fact, we may be guilty of failing to distinguish between the greater and the lesser of two admitted evils. The logic of the dilemma itself cannot decide this choice for us. Instead, we must bring to bear empirical inquiry and imagination to the evaluation of the grounds of the dilemma itself.

Writers commonly use the term dilemma without explicitly formulating the dilemma to which they refer, leaving it for the readers to do. And sometimes, what is called a dilemma really isn’t one. (Remember the dog’s tail? Calling it a leg doesn’t make it a leg.) As an example, consider the plight of Sophie in William Styron’s novel, Sophie’s Choice. The scene is Birkenau, the main Nazi extermination camp during World War II. Among the thousands arriving at the prison gates are Sophie and her two children, Jan and Eva. On the train platform a Nazi SS medical officer confronts them. He will decide which are the lucky ones; they will live to work in the camp. The rest will go to their death in the gas chambers. When Sophie insists she is Polish but not Jewish, the officer says she may choose one of her children to be saved. Which of the two should she save? On what basis ought Sophie resolve her dilemma? It looks as if she has only two alternatives, each of which presents an agonizing outcome. Or is there a third way out?

342

Finally, one of the most powerful and dramatic forms of argument is reductio ad absurdum (from the Latin, meaning “reduction to absurdity”). The idea of a reductio argument is to disprove a proposition by showing the absurdity of its inevitable conclusion. It is used, of course, to refute your opponent’s position and prove your own. For example, in Plato’s Republic, Socrates asks an old gentleman, Cephalus, to define right conduct. Cephalus says that it consists of paying your debts and keeping your word. Socrates rejects this answer by showing that it leads to a contradiction. He argues that Cephalus cannot have given the correct answer because if we believe that he did, we will quickly encounter contradictions; in some cases, when you keep your word you will nonetheless be doing the wrong thing. For suppose, says Socrates, that you borrowed a weapon from a man, promising to return it when he asks for it. One day he comes to your door, demanding his weapon and swearing angrily that he intends to murder a neighbor. Keeping your word under those circumstances would be absurd, Socrates implies, and the reader of the dialogue is left to infer that Cephalus’s definition, which led to this result, has been refuted.

Let’s take a closer look at another example. Suppose you are opposed to any form of gun control, whereas I am in favor of gun control. I might try to refute your position by attacking it with a reductio argument. To do that, I start out by assuming the very opposite of what I believe or favor; instead, I try to establish a contradiction that results from following out the consequences of this initial assumption. My argument might look like this:

13. Let’s assume your position — namely, that there ought to be no legal restrictions of any kind on the sale and ownership of guns. That means that you’d permit having every neighborhood hardware store sell pistols and rifles to whoever walks in the door. But that’s not all. You apparently also would permit selling machine guns to children, antitank weapons to lunatics, small-bore cannons to the nearsighted, as well as guns and ammunition to anyone with a criminal record. But this is utterly preposterous. No one could favor such a dangerous policy. So the only question worth debating is what kind of gun control is necessary.

Now in this example, my reductio of your position on gun control is not based on claiming to show that you have strictly contradicted yourself, for there is no purely logical contradiction in opposing all forms of gun control. Instead, what I have tried to do is to show that there is a contradiction between what you profess — no gun controls at all — and what you probably really believe, if only you’ll stop to think about it — which is that no lunatic should be allowed to buy a loaded machine gun.

My refutation of your position rests on whether I succeed in establishing an inconsistency among your own beliefs. If it turns out that you really believe lunatics should be free to purchase guns and ammunition, then my attempted refutation fails.

In explaining reductio ad absurdum, we have had to rely on another idea fundamental to logic, that of contradiction, or inconsistency. (We used this idea, remember, to define validity in Chapter 3. A deductive argument is valid if and only if the process of affirming the premises and denying the conclusion results in a contradiction.) The opposite of contradiction is consistency, a notion of hardly less importance to good reasoning than validity. These concepts deserve a few words of further explanation and illustration. Consider this pair of assertions:

343

14. Abortion is homicide.

15. Racism is unfair.

No one would plausibly claim that we can infer or deduce 15 from 14, or, for that matter, 14 from 15. This almost goes without saying because there is no evident connection between these two assertions. They are unrelated assertions; logically speaking, they are independent of each other. In such cases the two assertions are mutually consistent; that is, both could be true — or both could be false. But now consider another proposition:

16. Euthanasia is not murder.

Could a person assert 14 (Abortion is homicide) and also assert 16 (Euthanasia is not murder) and be consistent? This question is equivalent to asking whether one could assert the conjunction of these two propositions — namely:

17. Abortion is homicide, and euthanasia is not murder.

It’s not so easy to say whether 17 is consistent or inconsistent. The kinds of moral scruples that might lead a person to assert one of these conjuncts (i.e., one of the two initial propositions, Abortion is homicide and Euthanasia is not murder) might lead to the belief that the other one must be false and thus to the conclusion that 17 is inconsistent. (Notice that if 14 were the assertion that Abortion is murder, instead of Abortion is homicide, the problem of asserting consistently both 14 and 16 would be more acute.) Yet if we think again, we might imagine someone being convinced that there is no inconsistency in asserting that Abortion is homicide, say, and that Euthanasia is not murder, or even the reverse. (For instance, suppose you believed that the unborn deserve a chance to live and that putting terminally ill persons to death in a painless manner and with their consent confers a benefit on them.)

Let us generalize: We can say of any set of propositions that they are consistent if and only if all could be true together. (Notice that it follows from this definition that propositions mutually imply each other, as do Seabiscuit was America’s fastest racehorse and America’s fastest racehorse was Seabiscuit.) Remember that, once again, the truth of the assertions in question doesn’t matter. Two propositions can be consistent or not, quite apart from whether they are true. Not so with falsehood: It follows from our definition of consistency that an inconsistent proposition must be false. (We have relied on this idea in explaining how a reductio ad absurdum argument works.)

Assertions or claims that are not consistent can take either of two forms. Suppose you assert proposition 14, that abortion is homicide, early in an essay you are writing, but later you assert that

18. Abortion is harmless.

344

You have now asserted a position on abortion that is strictly contrary to the one with which you began — contrary in the sense that both assertions 14 and 18 cannot be true. It is simply not true that if an abortion involves killing a human being (which is what homicide strictly means), then it causes no one any harm (killing a person always causes harm — even if it is excusable, justifiable, not wrong, the best thing to do in the circumstances, and so on). Notice that although 14 and 18 cannot both be true, they can both be false. In fact, many people who are perplexed about the morality of abortion believe precisely this. They concede that abortion does harm the fetus, so 18 must be false; but they also believe that abortion doesn’t kill a person, so 14 must also be false.

Let’s consider another, simpler case. If you describe the glass as half empty and I describe it as half full, both of us can be right; the two assertions are consistent, even though they sound vaguely incompatible. (This is the reason that disputing over whether the glass is half full or half empty has become the popular paradigm of a futile, purely verbal disagreement.) But if I describe the glass as half empty whereas you insist that it is two-thirds empty, then we have a real disagreement; your description and mine are strictly contrary, in that both cannot be true — although both can be false. (Both are false if the glass is only one-quarter full.)

This, by the way, enables us to define the difference between a pair of contradictory propositions and a pair of contrary propositions. Two propositions are contrary if and only if both cannot be true (though both can be false); two propositions are contradictory if and only if they are such that if one is true the other must be false, and vice versa. Thus, if Jack says that Alice Walker’s The Color Purple is a better novel than Mark Twain’s Huckleberry Finn, and Jill says, “No, Huckleberry Finn is better than The Color Purple,” she is contradicting Jack. If what either one of them says is true, then what the other says must be false.

A more subtle case of contradiction arises when two or more of one’s own beliefs implicitly contradict each other. We may find ourselves saying “Travel is broadening,” and saying an hour later “People don’t really change.” Just beneath the surface of these two beliefs lies a self-contradiction: How can travel broaden us unless it influences — and changes — our beliefs, values, and outlook? But if we can’t really change ourselves, then traveling to new places won’t change us, either. (Indeed, there is a Roman saying to the effect that travelers change the skies above them, not their hearts.) “Travel is broadening” and “People don’t change” collide with each other; something has to give.

Our point, of course, is not that you must never say today something that contradicts something you said yesterday. Far from it; if you think you were mistaken yesterday, of course you will take a different position today. But what you want to avoid is what George Orwell called doublethink in his novel 1984: “Doublethink means the power of holding two contradictory beliefs in one’s mind simultaneously, and accepting them both.”

Genuine contradiction, and not merely contrary assertion, is the situation we should expect to find in some disputes. Someone advances a thesis — such as the assertion in 14, Abortion is homicide — and someone else flatly contradicts it by the simple expedient of negating it, thus:

19. Abortion is not homicide.

345

If we can trust public opinion polls, many of us are not sure whether to agree with 14 or with 19. But we should agree that whichever is true, both cannot be true, and both cannot be false. The two assertions, between them, exclude all other possibilities; they pose a forced choice for our belief. (Again, we have met this idea, too, in a reductio ad absurdum.)

Now it is one thing for Jack and Jill in a dispute or argument to contradict each other. It is quite another matter for Jack to contradict himself. One wants (or should want) to avoid self-contradiction because of the embarrassing position that results: Once I have contradicted myself, what are others to believe I really believe? What, indeed, do I believe, for that matter?

It may be, as Emerson observed, that a “foolish consistency is the hobgoblin of little minds” — that is, it may be shortsighted to purchase a consistency in one’s beliefs at the expense of flying in the face of common sense. But making an effort to avoid a foolish inconsistency is the hallmark of serious thinking.

While we’re speaking of inconsistency, let’s spend a moment on paradox. The word refers to two different things:

An example of the first might be “Evaluations concerning quality in literature are all a matter of personal judgment, but Shakespeare is the world’s greatest writer.” It is hard to make any sense out of this assertion. Contrast it with a paradox of the second sort, a seeming contradiction that may make sense, such as “The longest way around is the shortest way home,” or “Work is more fun than fun,” or “The best way to find happiness is not to look for it.” Here we have assertions that are striking because as soon as we hear them we realize that although they seem inconsistent and self-defeating, they contain (or may contain) profound truths. Paradoxes of this second sort are especially common in religious texts, where they may imply a mysterious reality concealed by a world of contradictory appearances. Examples are “Some who are last shall be first, and some who are first shall be last” (Jesus, quoted in Luke 13:30), and “Death, thou shalt die” (the poet John Donne, alluding to the idea that the person who has faith in Jesus dies to this world but lives eternally). If you use the word paradox in your own writing — for instance, to characterize an argument that you’re reading — be sure that the reader will understand in which sense you’re using the word. (And, of course, you won’t want to write paradoxes of the first, self-contradictory sort.)