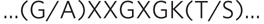Most Protein Structures Are Solved by X-Ray Crystallography

Max Perutz, 1914–2002 (left); John Kendrew, 1917–1997 (right)
The use of x-ray crystallography to determine the structure of proteins was pioneered by Max Perutz and John Kendrew, who solved the structures of hemoglobin and myoglobin. This was an enormously difficult task at the time. The equipment and techniques continue to be improved, and more than 50,000 protein structures are now available in the Protein Data Bank, a repository of information on protein structures. Of all known protein structures, over 90% were determined by x-ray crystallography (see Highlight 4-2). There is no theoretical limit to the size of protein that can be analyzed by this method.
Amplifying Diffracted X Rays X-ray crystallography illuminates a protein crystal with an x-ray beam, and the diffracted x rays are collected for analysis (Figure 4-26a). Diffracted x rays travel in every direction and thus normally create a blur on a detector. But in a crystal, trillions of protein molecules are aligned in a regular lattice, and therefore some of the diffracted x rays combine and add up in a process called constructive interference, forming a reflection spot on a film or detector. Each reflection spot in a diffraction pattern is produced by the summation of diffracted x rays in the unit cell, the smallest regularly repeating unit in the crystal (Figure 4-26b). The unit cell can be as small as a single protein molecule, but it often consists of two or more identical protein molecules. The spacing of reflections is related to atomic distance in the unit cell. To obtain a sufficient number of reflections for determining the protein structure, the crystal is rotated during x-ray irradiation. Tens of thousands of reflections are usually collected to solve one protein structure.
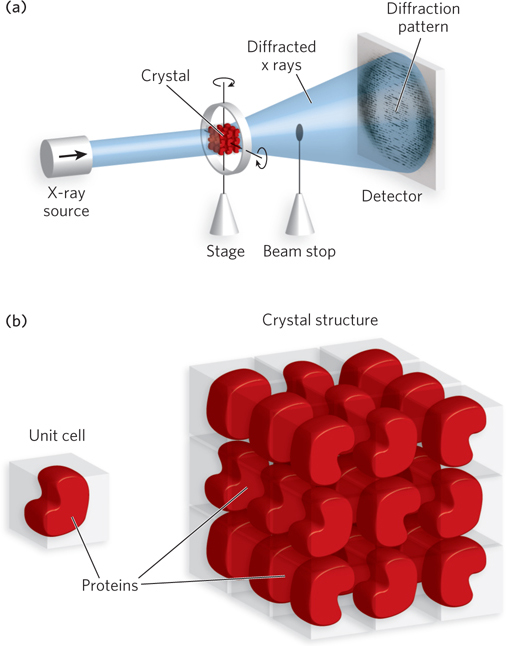
Figure 4-26: Protein crystals and diffraction patterns. (a) Protein crystals produce a diffraction pattern when x rays are passed through them. In x-ray crystallography, the crystal is rotated in all directions, and diffracted x rays are collected by a detector. X rays that pass through the crystal without diffraction are blocked from hitting the detector by a beam stop. (b) The unit cell, or repeating unit in the lattice of a protein crystal, may contain one or more protein molecules.
Reconstructing the Protein Image An object illuminated in a light microscope also produces a diffraction pattern, but it is not visible, because the diffracted light is recombined into an image with a converging lens. Electron microscopy works in a similar fashion, using magnets to refocus the diffracted electrons into an image. However, no lens can recombine diffracted x rays. Instead, the diffraction pattern is recombined into an image by a mathematical converging series, called a Fourier series, that acts, mathematically, like a converging lens. X rays are photons and therefore behave as sine waves, each of which has an amplitude, a wavelength, and a phase. The amplitude is the height of the wave and the wavelength is the distance between waves. The phase describes how wavelengths align. For example, two waves of the same wavelength could be completely out of phase with one another, with the crest of one occurring in the trough of the other; or they could be in phase, in which case their wave crests are additive. These three parameters—amplitude, wavelength, and phase—are required for the Fourier series. The wavelength, λ (lambda), is the same as that of the x-ray beam used to illuminate the crystal, and the amplitude, A, is calculated from the spot intensity, I (I = A2). But when a diffracted x-ray wave hits the detector, the wave collapses and the phase is lost. The experimenter must determine the phase of the x-ray waves before the crystal structure can be solved. There are several methods for determining the phase of each reflection, which we will not go into here.
The reconstructed image is displayed on a molecular graphics console as a volume encased in a meshwork referred to as an electron density map (Figure 4-27): the higher the resolution, the greater the detail contained in the electron density map. Paradoxically, the reflections in the diffraction pattern that carry the highest resolution are those that are farthest from the center.
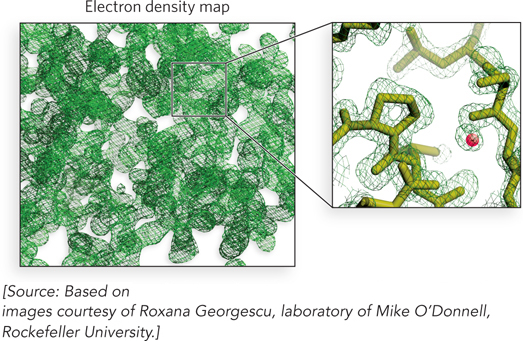
Figure 4-27: An electron density map. An electron density map (left) contains too much information to analyze when viewed all at once. The experimenter focuses instead on one small region at a time (right) and fits the polypeptide backbone into the density. Shown here are molecules that lie in the outlined portion of the electron density map. The small red sphere is an ordered water molecule—a water molecule that is held in one place and thus can be visualized.
Examples of electron density maps of a tryptophan side chain in a protein, obtained by using reflections at increasing distances from the center of a diffraction pattern, are shown in Figure 4-28. Using reflections in the diffraction pattern that correspond to a resolution of 4 Å between atoms in an electron density map, the resolution is insufficient to trace the path of the peptide backbone or to place most of the side chains. Using reflections that correspond to a resolution of 3 Å, the peptide backbone is discernible as a continuous ribbon. Secondary structural elements are visible, and the general shape of side chains is often apparent, but there are usually some disordered regions in loops that cause breaks in the density and prevent a continuous chain trace. A range of 2.2 to 3.0 Å resolution is required to get the most complete information on a protein’s structure.

Figure 4-28: The relationship between resolution and diffraction pattern. The dotted circles in the diffraction pattern (top) represent the locations of reflections responsible for two different resolutions of an electron density map. The maps below show four different resolutions. The area of electron density corresponds to Trp123 of the E. coli DNA polymerase β subunit. Positions of the atoms of the Trp residue in the final model are shown in the four panels.
The Initial Model The three-dimensional protein structure inferred from the electron density map is known as the initial model. In the early stages of analysis, the initial model is hypothetical. To build the model, the known amino acid sequence of the protein must be fitted into the electron density mesh. Model building is aided by graphics on a computer screen, but it is mostly performed manually and requires the skill and patience of the experimenter. Because the peptide bond is planar, a peptide bond “ruler” helps identify the Cα atoms. To position the primary sequence in the electron density map, the experimenter looks for unusual arrangements of large, characteristic side chains. The remaining side chains are then filled in, and each is adjusted into the electron density. The resulting initial model is far from perfect, but errors are minimized in the next stage, the refinement process.
Refinement Improvements in the electron density map are generated by refinement. Refinement is an iterative process (Figure 4-29). It starts by taking the model and building a model crystal from it computationally (in silico). Then the Fourier series is used to compute a diffraction pattern for the model crystal, and the position and intensity of each calculated reflection are compared with the observed diffraction pattern. The difference between the calculated and observed values yields a measurement of the error in the model, referred to as an R factor (R for residual error). At the first iteration, the R factor value is usually 0.4 to 0.5. Although refinement theoretically has no ending, in practice, structures are refined to an R factor value of 0.15 to 0.25.
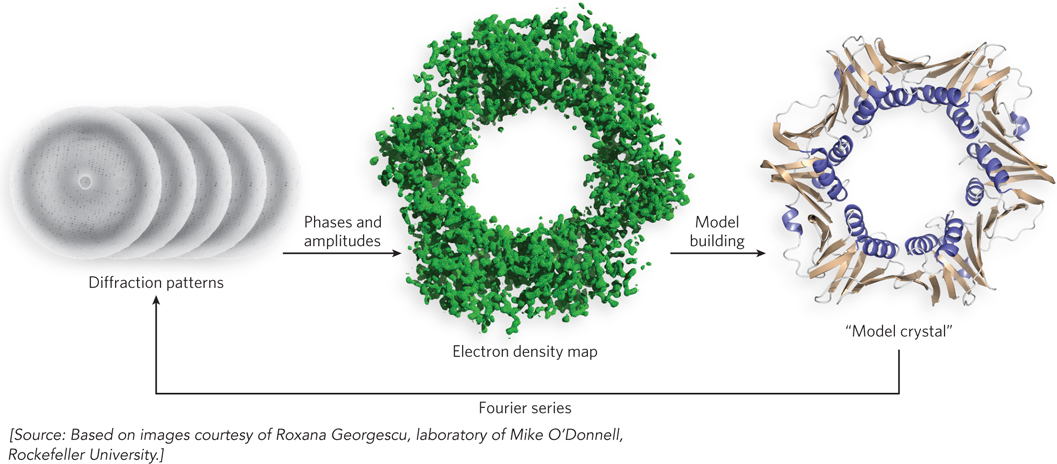
Figure 4-29: Refinement. During refinement in x-ray diffraction analysis, the initial model of the protein structure is used to calculate the theoretical diffraction pattern it would produce, using a Fourier series. The phases are then adjusted to obtain a pattern close to the observed diffraction pattern. The adjusted phases generate a more detailed electron density map, thus allowing more precise positioning of amino acid residues in the model. The process is repeated several times until the residual error (R factor) between observed and calculated diffraction patterns is reduced to an acceptable value.
The physical environment within a crystal is not identical to that in a solution or in a living cell, so the conformation of a protein in a crystal could, in principle, be affected by nonphysiological factors such as incidental protein-protein contacts. However, when structures derived from crystal analysis are compared with structural information obtained by NMR (described below), the crystal-derived structure almost always represents a functional conformation of the protein.
Smaller Protein Structures Can Be Determined by NMR
An important complementary method for determining protein structure is nuclear magnetic resonance (NMR). NMR is performed on proteins in solution, which is an advantage over x-ray crystallography because protein crystals can be difficult to obtain. However, only relatively small protein structures can be solved by NMR (Mr < 25,000, or ∼200 amino acids).
Obtaining Primary Data The primary data from NMR are radio-frequency lightwave emissions from atomic nuclei. Only certain atoms, including 1H, 13C, 15N, 19F, and 31P, possess the kind of nuclear spin that gives rise to an NMR signal. The technique involves placing the protein sample in a strong magnetic field, which aligns the spins of all the nuclei of the particular atom under study. Then the sample is pulsed with radio-frequency radiation to excite the nuclei. As the nuclei relax, they emit radiowaves, which are detected and recorded. After many repetitions in rapid succession, the data are averaged. Repeated pulses of irradiation and collected emitted radiowaves are summed, thus increasing the signal-to-noise ratio to produce an NMR spectrum. The emissions are plotted as a spectrum of chemical shifts, expressed as parts per million (ppm). The chemical shift of a nucleus is sensitive to its environment and therefore carries environmental signatures that can be used to obtain structural information.
1H is particularly important in NMR experiments because of its high sensitivity and natural abundance. However, even a small protein has hundreds of 1H atoms, typically resulting in a one-dimensional NMR spectrum too complex for analysis (Figure 4-30a). Structural analysis of proteins became possible with the advent of two-dimensional NMR techniques.
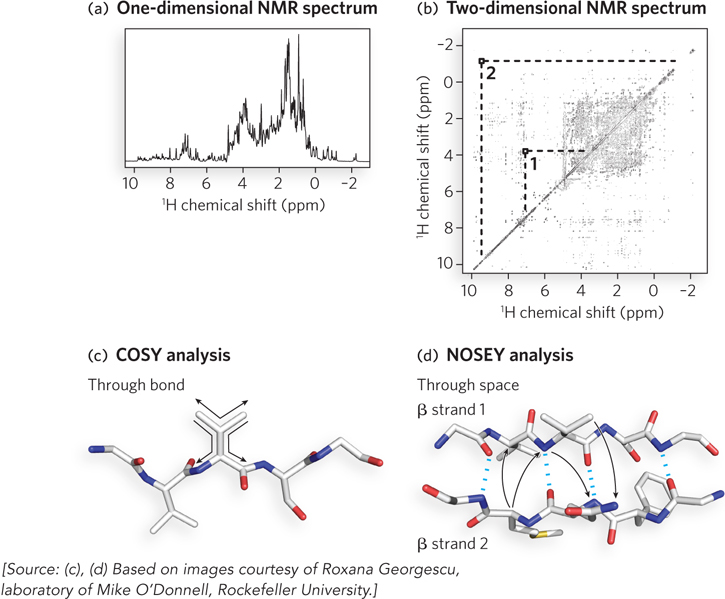
Figure 4-30: NMR spectra and protein-protein interactions. (a) A one-dimensional NMR spectrum of a globin from a marine bloodworm. The spectrum represents the amount of chemical shift for each proton in a peptide segment. For a protein, the proton signals do not resolve in a one-dimensional spectrum, as indicated by the many overlapping peaks. (b) A two-dimensional NMR spectrum of the same globin molecule. The spots and their intensities that lie along the diagonal line are equivalent to the data contained in the peaks of the one-dimensional spectrum. The off-diagonal peaks (e.g., peaks 1 and 2) are nuclear Overhauser effect (NOE) signals generated by close-range interactions of 1H atoms that generate signals quite distant in the one-dimensional spectrum. (c) The two-dimensional COSY analysis identifies proton-proton signals through one or two covalent bonds (“through-bond” signals) and thus is limited to individual amino acid units. (d) The NOESY analysis yields NOE signals resulting from proton-proton interactions occurring through empty space (“through-space” signals) and thus identifies protons close in space but not necessarily close in the primary sequence.
Many variations of two-dimensional NMR are performed by using different combinations of radio-frequency pulses and delays to separate the signals. In two-dimensional NMR, the data derived from the different pulses and delays are plotted along x and y axes, yielding a two-dimensional spectrum (Figure 4-30b). Instead of the plotting of peak height along the y axis, each spot carries a unique intensity that correlates with the peak height in the one-dimensional spectrum. The signals along the diagonal line through the two-dimensional spectrum are the same signals as in the one-dimensional spectrum, and the variation in intensity along the diagonal correlates with their peak heights. The signals that lie off the diagonal, called nonsequential signals, are derived by magnetization transfer between two protons that are close in space. In one type of two-dimensional NMR, called correlation spectroscopy (COSY), the signals allow the identification of protons connected by covalent bonds (Figure 4-30c). In two-dimensional nuclear Overhauser effect spectroscopy (NOESY), these nonsequential signals allow the measurement of distances through space between nearby atoms (Figure 4-30d). All we need to know for now is that the COSY signals allow the researcher to trace the polypeptide backbone and thus to assign signals to particular amino acids. The NOESY signals occur through space and do not travel through the bonds between atoms. Therefore, NOE signals can arise from residues that are far apart in the primary structure but close together in the tertiary structure (see Figure 4-30d). These through-space signals carry the most important information about the three-dimensional structure of the protein and are the main data used to solve protein structures by NMR.
Tertiary Structure Determination Once the chemical shifts that derive from the primary sequence have been assigned by COSY, the through-space NOE signals provide information that restrains the possible tertiary structure solutions—information that is referred to as a “restraint.” Restraints are absolutely essential to the prediction of tertiary structure. More than 1,000 restraints are required to predict a structure containing 100 residues or more. Although most of these restraints are NOE signals that represent protons close in space but distant in the primary sequence, another type of restraint is the torsion angles between residues, as obtained from the COSY spectrum. A third type of restraint is the known geometric restraints of all amino acids, such as chirality, van der Waals radii, and bond lengths.
With sufficient restraints, a structure can be predicted. First, a randomized configuration of the primary sequence is produced using the known geometry of the peptide bond and side-chain atoms. This still leaves a huge number of possible configurations, however, because the backbone N–Cα and Cα–C bonds are, to some degree, free to rotate. The computer program then tries to fold the chain in a way that best satisfies all the restraints, starting from those nearby in the sequence and proceeding to those that are farther apart. This procedure is repeated several times, each time starting with a different randomized configuration of the primary sequence. If the structure is substantially the same after each trial, then the number of restraints was sufficient to arrive at a unique solution.
Structures determined by NMR are usually shown as a group of closely related structures (Figure 4-31). The individual structures are arrived at by independent trials and represent the range of conformations consistent with the list of restraints. Although the uncertainty in structures generated by NMR is in part a reflection of the molecular vibrations (commonly called breathing) within a protein structure in solution, the observed variation is also due to errors or insufficiencies in the list of restraints. For example, the areas of greatest variation between different structures of a group usually signify areas with fewer restraints. For this reason, in NMR analyses, the total number of restraints is far more important than the accuracy of individual restraints.
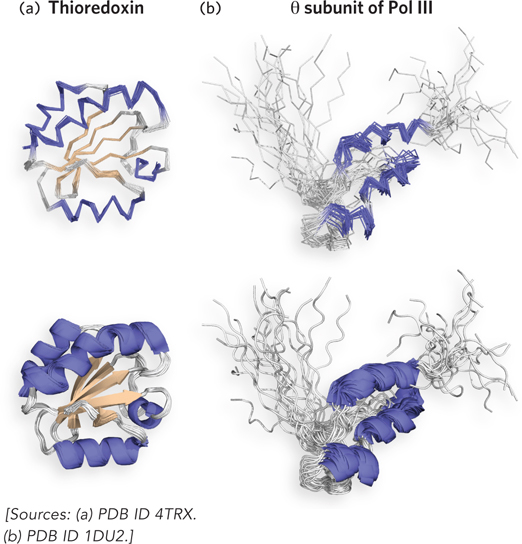
Figure 4-31: The structure of two proteins as determined by NMR. (a) Human thioredoxin (Mr 12,000). Multiple lines represent structures consistent with the restraints from the NMR data. One line is shown thicker than the rest to show the secondary elements within the structure. (b) The θ (theta) subunit (Mr 8,600) of DNA polymerase III (Pol III). The divergent models reflect the lack of restraints in disordered areas. The protein contains a region that lacked sufficient restraints to arrive at a unique solution and probably signifies a region of disordered residues.
Whenever a protein structure is determined by both x-ray crystallography and NMR, the structures generally agree well. In some cases, the precise locations of particular amino acid side chains on the protein exterior are different, often because of effects related to the packing of adjacent protein molecules in a crystal. The two techniques together are at the heart of the rapid increase in the availability of structural information on the macromolecules of living cells.
SECTION 4.5 SUMMARY
The two methods that reveal protein structure at atomic resolution are x-ray crystallography and nuclear magnetic resonance.
X-ray crystallography can be applied to a protein of any size, but it requires a protein crystal.
The diffraction pattern of x rays that have passed through a protein crystal must be recombined into an image mathematically, using the Fourier series.
NMR is performed on proteins in solution and can be applied only to small proteins (Mr < 25,000).
In NMR, the atomic nuclei are excited in a magnetic field, and emitted radiation is collected; some of the signals are sensitive to environment and contain structural information.
In NOESY and COSY, two types of two-dimensional NMR, atoms that are covalently bonded or otherwise in close proximity to one another are identified, and the distances between them are used to create a list of restraints from which a structure can be generated.
UNANSWERED QUESTIONS
Numerous protein structures have been determined, and one might think that, by now, researchers would have deciphered most of the rules about how proteins fold into their unique shapes. Yet, the information that directs how proteins fold and how they associate with their proper partners in a cell remains largely unknown and continues to be a highly active area of research. Here are some of the many questions being actively pursued.
What is the “code” in the primary sequence that determines how a protein folds? We know that the instructions for folding lie in the primary sequence. However, despite the large database of protein structures, we still do not know how these instructions are read. The problem lies in the relatively small difference in energy between the folded and unfolded states. Researchers remain hopeful that the “rules” of protein folding will someday be understood. Perhaps the accurate prediction of the structure adopted by a given sequence will be obtained by computations that draw on the vast empirical knowledge of structural folding patterns in proteins, combined with theoretical energy computations.
How do proteins “know” they are to form multiprotein complexes? Many of the important functions in a cell are performed by multiprotein complexes that act as machines to carry out complicated tasks. These tasks include central jobs such as transcription, replication, and translation. Given the thousands of different proteins in a cell, it is perplexing that particular subunits “know” how to join up, to the exclusion of others, to form these large complexes.
How do chaperones and chaperonins “know” when to bind a protein? Proteins that denature, or newly synthesized proteins that require assistance with folding, are targeted by chaperones and chaperonin complexes. However, most proteins contain disordered regions even when they are properly folded. We know little about how chaperones and chaperonins specifically target unfolded proteins, and even less about how these protein-folding assistants recognize when their job is done, or when to keep working.
Sequence Comparisons Yield an Evolutionary Roadmap from Bird Influenza to a Deadly Human Pandemic
Taubenberger, J.K., A.H. Reid, R.M. Lourens, R. Wang, G. Jin, and T.G. Fanning. 2005. Characterization of the 1918 influenza virus polymerase genes. Nature 437:889–893.
Worldwide pandemic outbreaks of flu can lead to millions of deaths. A virus has little to gain by killing its host, and, usually, the more deadly a virus is, the more recently it evolved. The evolution of a deadly virus has been intensively studied for influenza strains that cause pandemics.
A given influenza virus is typically confined to a certain host species, such as birds, horses, pigs, or humans—partly because cell surface receptors that allow entry of a virus are different in each species. However, some influenza strains evolve and jump the species barrier. Trouble for humans starts when the viruses also acquire efficient human-to-human transmissibility. This rare event can result in a worldwide influenza pandemic. About one to three such pandemics occur every century. How do these deadly viruses evolve? This can be determined from their genome sequences and comparisons with other influenza viruses.
The influenza virus genome consists of eight segments of RNA that encode 10 different proteins. Evolution is facilitated in a couple of ways: through errors introduced by the viral replicase, an RNA-dependent RNA polymerase that copies the RNA genome, and through genetic reassortment of RNA segments between two different viruses to form a novel virus. Genetic reassortment of RNA segments occurs when one host animal becomes infected by two different viruses at the same time. The pig, for example, has cell surface receptors that allow infection by both avian and human influenza viruses and thus may act as a “mixing vessel” to produce recombinant influenza viruses.
Comparative sequence analysis of the avian and human viruses responsible for the influenza pandemics of 1957 and 1968 reveals that the viruses evolved by genetic reassortment of two or three genes between an avian and a human virus. Both pandemic viral strains contained an avian PB1 gene, which encodes part of the viral replicase, a 1:1:1 protein complex composed of products of the PB1, PB2, and PA genes. However, a comparison of the PB2 protein sequences of influenza viruses from multiple sources reveals a human origin of the PB2 gene for the Asian flu pandemic of 1957 and the Hong Kong flu pandemic of 1968 (Figure 1). This result supports the hypothesis of a mixing vessel in the evolution of these viruses. Interestingly, the 1918 Brevig Mission strain, which resulted in the worst pandemic so far, follows a different evolutionary history. Hundreds of millions of people were infected during the 1918–1919 “Spanish flu” pandemic, resulting in the deaths of about 50 million people worldwide. Comparative analysis of all the genes of the 1918 Brevig Mission virus indicates that it did not evolve by genetic reassortment with a second virus but, instead, adapted to humans directly from an avian source.
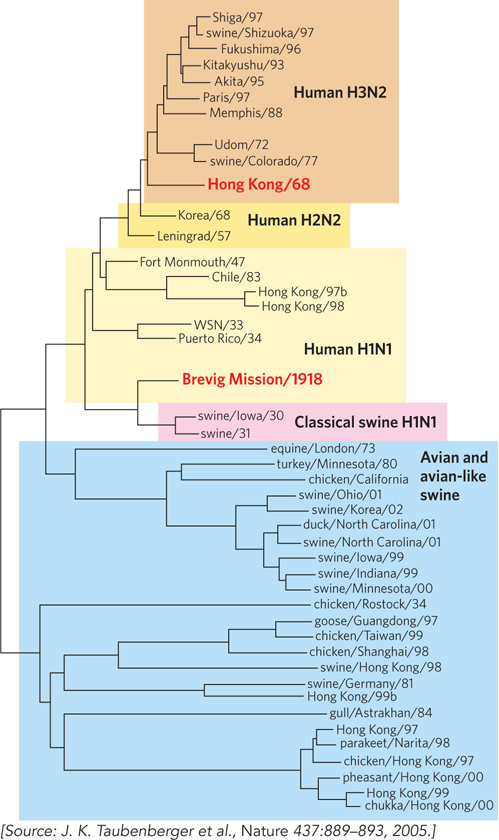
FIGURE 1 This phylogenetic tree of avian and human influenza viruses is based on sequence comparisons of the PB2 gene. Branch points indicate the place where two PB2 sequences diverged from a common ancestor. The 1918, 1957, and 1968 pandemics mentioned in the text are highlighted in red.
We Can Tell That a Protein Binds ATP by Looking at Its Sequence
Koonin, E.V. 1993. A superfamily of ATPases with diverse functions containing either classical or deviant ATP-binding motif. J. Mol. Biol. 229:1165–1174.
Saraste, M., P.R. Sibbald, and A. Wittinghofer. 1990. The P-loop: A common motif in ATP- and GTP-binding proteins. Trends Biochem. Sci. 15:430–434.
Wouldn’t it be handy to be able to figure out what role a protein plays without having to perform complicated experiments? Sequence comparisons can do just that. A classic example is the identification of an ATP/GTP-binding site, based on some characteristic features of ATP/GTP-binding proteins.
Many proteins that bind ATP or GTP have several structural features in common. The P-loop is a conserved, glycine-rich sequence that forms a loop and connects a β strand to an α helix (Figure 2). The P-loop (phosphate-binding loop) interacts with the phosphates of ATP or GTP (Figure 3), and the presence of a P-loop sequence usually indicates that the protein’s function involves the use of ATP or GTP. The P-loop is found in association with the nucleotide-binding Rossmann fold motif.
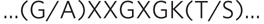
FIGURE 2 The P-loop consensus sequence (i.e., the sequence found in many ATP-binding proteins). X means any amino acid; a pair of residues in parentheses means that one can substitute for the other—for example, G/A means either G or A (Gly or Ala) in that position.
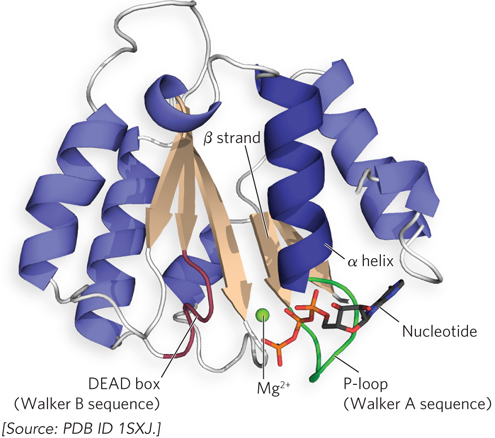
FIGURE 3 This ribbon representation of the ATP-binding RFC2 subunit of the yeast RFC clamp loader, which loads sliding clamps onto DNA for DNA polymerase (discussed in Chapter 11), highlights the features of the Rossmann fold motif that participate in nucleotide binding. The P-loop interacts with the nucleotide, and the DEAD box binds ions that assist in nucleotide hydrolysis.
The P-loop is also referred to as a Walker A sequence. It is often followed in the protein’s primary sequence (after a variable number of residues) by a Walker B sequence, sometimes called a DEAD box (for the amino acid sequence Asp–Glu–Ala–Asp, in one-letter symbols), which contains acidic residues that bind magnesium ions and assist in ATP or GTP hydrolysis. These two sequences are widespread in proteins that function with ATP or GTP. A few examples are eukaryotic Ras family GTP-binding proteins and eukaryotic and bacterial recombinases and mismatch repair proteins. Despite the widespread use of the P-loop motif, however, some proteins bind ATP using sequences that are unrelated to the Walker A motif.
Disulfide Bonds Act as Molecular Cross-Braces to Stabilize a Protein
Matsumura, M., G. Signor, and B.W. Matthews. 1989. Substantial increase of protein stability by multiple disulfide bonds. Nature 342:291–293.
In building construction, cross-braces make bridges and walls stronger and sturdier. Proteins, too, utilize cross-braces. A disulfide bond connects two regions of one or more polypeptide chains within a protein and probably acts as a molecular cross-brace to enhance protein stability. But how would a researcher determine whether a disulfide bond really does work as a stabilizing cross-brace?
Brian Matthews’s laboratory at the University of Oregon examined disulfides for cross-brace function by engineering pairs of Cys residues into T4 lysozyme and then measuring their effect on protein stability (a mutant protein with three disulfide bonds is shown in Figure 4a). The proteins were crystallized to allow detection of structural alterations by x-ray diffraction, and protein stability was measured by circular dichroism (CD) spectroscopy at different temperatures. CD spectroscopy measures the amount of secondary structure in a protein and allows the researcher to follow the loss of α-helical content that accompanies protein denaturation.
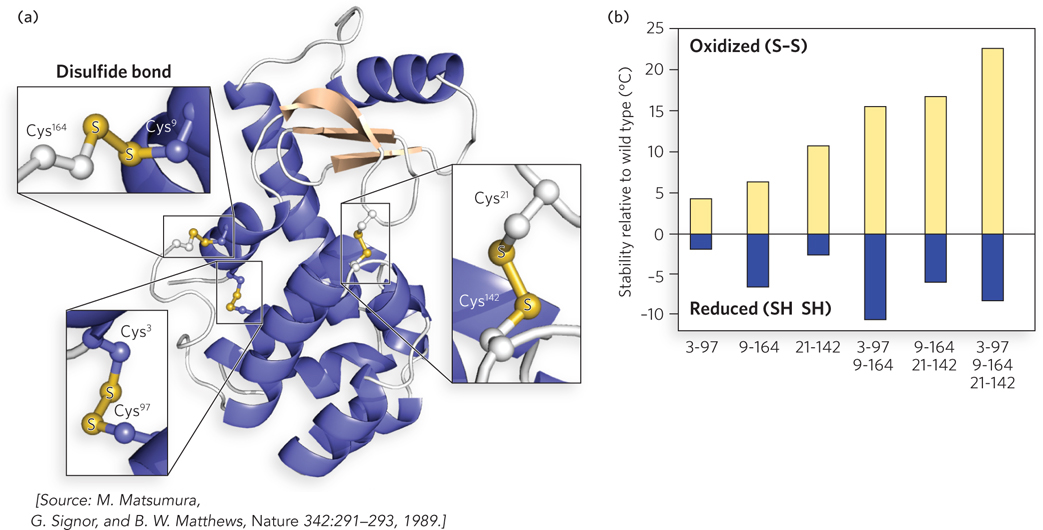
FIGURE 4 (a) Pairs of Cys residues (numbered for their position in the primary sequence) were engineered into T4 lysozyme. This mutant has three disulfide bonds. (b) Additional disulfide bonds stabilize protein structure relative to wild-type lysozyme. The numbers below the plot indicate the positions of the Cys residues involved in the disulfide bonds. The rightmost column shows the results for the three-disulfide mutant protein in (a). The stability of these proteins is indicated by the temperature at which the protein loses its activity, compared with wild type.
Mutant proteins with a single disulfide bond had the same structure as wild-type lysozyme, with only small distortions at the replacement sites. Reduction of the disulfide bond (forming two unlinked Cys residues) resulted in a less-stable protein compared with wild-type lysozyme, indicating that Cys substitution had slightly destabilized each mutant protein. But in the oxidized form, the disulfide cross-link greatly increased the stability of several mutant proteins over the wild-type lysozyme. Addition of multiple disulfide cross-links to the wild-type lysozyme gave an additive effect in the stability of the mutant proteins (Figure 4b).
These elegant structural and biochemical studies demonstrated that disulfide bonds really do act as molecular cross-braces to enhance the stability of a protein. Antibodies, for example, contain many disulfide bonds, and we may assume that these bonds stabilize the proteins as they circulate in blood, outside the protective confines of the cell membrane.