Section 12.3 Exercises

CLARIFYING THE CONCEPTS

Question 12.97

1. Explain the difference between the variable of interest and the blocking factor. What is another term for the variable of interest? For the blocking factor? (p. 694)

12.3.1

The variable of interest is the variable we are interested in studying, and the blocking factor is a variable that is not of primary interest to the researcher but is included in the ANOVA in order to improve the ability of the ANOVA to find significant differences among the treatment means. Treatment. Nuisance factor.

Question 12.98

2. What do we do in a randomized block design ANOVA? (p. 694)

Question 12.99

3. Explain why a large SSE is bad if we want to reject the null hypothesis in ANOVA. (p. 697)

12.3.3

We reject when the is small. The smaller SSE is, the larger is and therefore the smaller the is.

Question 12.100

4. Explain how a larger statistic leads to a more likely rejection of the null hypothesis in ANOVA. (p. 697)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 5–10 Example 11 Randomized block design
(RBD)
Exercises 11–13 Example 12 Demonstrating how RBD
works

For Exercises 5–8, use the indicated randomized block design ANOVA output to test, using level of significance , whether the treatment means differ.

  1. Provide the hypotheses and the rejection rule.
  2. Find the relevant -value; provide the conclusion and the interpretation.

Question 12.101

5.

image

12.3.5

(a) : Not all of the population means are equal. Reject if . (b) The , which is ; therefore we reject . There is evidence at level of significance that the population means are not all equal.

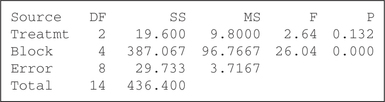
Question 12.102

6.

image

Question 12.103

7.

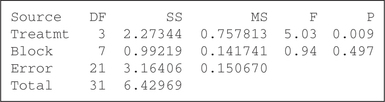
image

12.3.7

(a) : Not all of the population means are equal. Reject if . (b) The , which is ; therefore we reject . There is evidence at level of significance that the population means are not all equal.

Question 12.104

8.

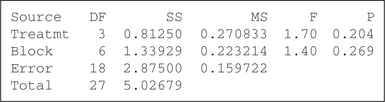
image

For Exercises 9 and 10, for the indicated partially completed randomized block ANOVA table, do the following:

700

  1. Provide the hypotheses.
  2. Complete the missing entries in the table.
  3. Use technology to find the -value. For level of significance , provide the conclusion and the interpretation.

Question 12.105

9.

Source Sum of
square		 Degrees of
freedom		 Mean
squares
Treatments 90 — 45 —
Blocks 50 — —
Error — 8 7.5
Total — 15

12.3.9

(a) : Not all of the population means are equal. Reject if . (b) Answers to missing values are in red.

Source Sum of
squares		 Degrees of
freedom		 Mean
square
Treatments 90 2 45 6
Blocks 50 5 10
Error 60 8 7.5
Total 200 15

(c) The , which is ; therefore we reject . There is evidence at level of significance that the population means are not all equal.

Question 12.106

10.

Source Sum of
square		 Degrees of
freedom		 Mean
squares
Treatments — 3 — —
Blocks — 6 40
Error 216 — —
Total 636 —

For Exercises 11 and 12, do the following:

  1. Reconstruct the corresponding one-way ANOVA table.
  2. Perform the one-way ANOVA using level of significance . Provide the hypotheses, the conclusion, and the interpretation.
  3. Is the conclusion from the one-way ANOVA different from that of the RBD analysis? Did the RBD help to find significance?

Question 12.107

11. The randomized block design ANOVA table in Exercise 9

12.3.11

(a)

Source Sum of
squares		 Degrees of
freedom		 Mean
square
Treatments 90 2 45 5.3182
Error 110 13 8.4615
Total 200 15

(b) : Not all of the population means are equal. Reject if . The , which is ; therefore we reject . There is evidence at level of significance that the population means are not all equal. (c) The conclusions are the same for both tests. No.

Question 12.108

12. The randomized block design ANOVA table in Exercise 10

Question 12.109

13. Verify that, in general, equals the sum of and . (Hint: .)

12.3.13

APPLYING THE CONCEPTS

Question 12.110

veggieprices

14. Vegetable Prices. Is there a difference in the mean price of vegetables from year to year? The table contains the price per pound (in dollars) for six different vegetables in June 2012, June 2013, and June 2014. Test, using the randomized block design at level of significance , whether the population mean price is the same for all three years.

2012 2013 2014
Beans 1.44 1.40 1.48
Broccoli 1.68 1.73 1.77
Lettuce 0.90 0.93 1.12
Sweet Peppers 2.45 2.17 2.59
Potatoes 0.68 0.65 0.69
Tomatoes 1.49 1.47 1.68
Table 12.39: Source: U.S. Department of Agriculture.

Question 12.111

worldmath

15. Eighth-Grade Math Scores Worldwide. Have worldwide eighth-grade math scores been changing? The table contains the TIMMS average math score for eighth-graders in five countries, for the years 1995, 2007, and 2011. Test, using the randomized block design at level of significance , whether the population mean math score differs across the three years.

1995 2007 2011
Singapore 609 593 611
Japan 581 570 570
Russia 524 512 539
USA 492 508 509
Sweden 540 491 484
Table 12.40: Source: National Center for Education Statistics.

12.3.15

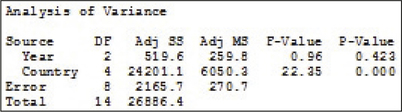
image

: Not all the population means are equal. Reject if the .

.

.

The is not . Therefore we do not reject . There is not enough evidence to conclude at level of significance that not all of the population mean math scores are the same for all three years.

Question 12.112

healthinschildren

16. Health Insurance: Children Not Covered. The following table contains the number of children under 18 who are not covered by health insurance, for a sample of six states, for the years 2010, 2011, and 2012 (in thousands). Test, using the randomized block design at level of significance , whether the population mean number of children not covered by health insurance is the same for all three years.

2010 2011 2012
Alabama 103 86 94
Florida 566 516 527
Georgia 249 278 321
Michigan 122 123 78
New York 352 284 240
Virginia 157 111 108
Table 12.41: Source: U.S. Census Bureau.

Question 12.113

17. Vegetable Prices. Refer to Exercise 14.

  1. Test whether the population mean price is the same for all three years, using a one-way ANOVA and level of significance .
  2. Compare your conclusions in Exercises 14 and 17(a). Did the randomized block design help us to find significance?

12.3.17

(a)

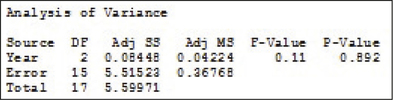
image

: Not all the population means are equal. Reject if the .

.

.

The is not . Therefore we do not reject . There is not enough evidence to conclude at level of significance that not all of the population mean prices of the vegetables are the same for all three years.

(b) Yes.

Question 12.114

18. Eighth-Grade Math Scores Worldwide. Refer to Exercise 15.

  1. Test whether the population mean math score differs across the three years, using a one-way ANOVA and level of significance .
  2. Compare your conclusions in Exercises 15 and 18(a). Did the randomized block design help us to reject the null hypothesis?

Question 12.115

19. Health Insurance: Children Not Covered. Refer to Exercise 16.

  1. Test whether the population mean number of children without health insurance is the same for all three years, using a one-way ANOVA and level of significance .
  2. Compare your conclusions in Exercises 16 and 19(a). Did the randomized block design help us to find significance?

12.3.19

(a)

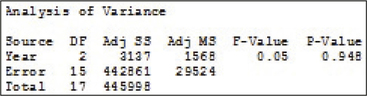
image

: Not all the population means are equal. Reject if the .

.

.

The p-value = 948 is not . Therefore we do not reject . There is not enough evidence to conclude at level of significance that not all of the population mean number of children not covered by health insurance are the same for all three years.

(b) No.

701

Question 12.116

businessvalue

20. Measures of Business Value. The following table contains three measures of the value of a business: the market capitalization, the firm value, and the business enterprise value (in millions of dollars).

  1. Use one-way ANOVA to test, at level of significance , whether the population mean values differ among the three measures.
  2. Notice how much some of the larger firms (like Caterpillar) differ from some of the smaller firms (like Abercrombie & Fitch) for all three measures. This indicates that there is variability among the firms. Let us account for this variability by using the firms as blocks and testing, using the randomized block design at level of significance , whether the population mean values differ among the three measures.
  3. Did accounting for the variability among the firms help us to find significant differences among the three measures of firm value?
Market
cap		 Firm
value		 Enterprise
value
Abercrombie & Fitch 3.1 3.2 2.7
Caterpillar 36.3 71.9 69.1
CIGNA 10.0 12.1 10.7
Delta Air Lines 9.2 25.8 21.3
Nissan Motors 38.2 90.0 82.4
Repsol Petroleum 32.6 50.2 45.5
Table 12.42: Source: U.S. Federal Trade Commission, 2009.