4 Correlation and Regression

Section 4.1 Exercises

CLARIFYING THE CONCEPTS

Question 4.1

1. When investigating the relationship between two quantitative variables, what graph should you use first? (p. 188)

4.1.1

Scatterplot

Question 4.2

2. In your own words, explain what the correlation coefficient measures. What is the symbol that we use for the correlation coefficient? (p. 192)

Question 4.3

3. What is the range of values the correlation coefficient can take? (p. 195)

4.1.3

Between −1 and 1, inclusive

Question 4.4

4. What do the following values of $r$ indicate about the relationship between two variables? What can we say about the variables?

A value of $r$ close to 1 (p. 196)
A value of $r$ close to −1 (p. 197)
A value of $r$ close to 0 (p. 197)

Question 4.5

5. Why do we call $x$ the predictor variable? (p. 188)

4.1.5

Often, the value of the $x$ variable can be used to predict or estimate the value of the $y$ variable.

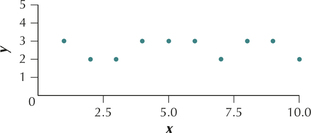
Question 4.6

6. Suppose two quantitative variables have a positive relationship. What can we say about the values of the $y$ variable as the $x$ variable increases? (p. 190)

Question 4.7

7. Suppose two quantitative variables have a negative relationship. What can we say about the values of the $y$ variable as the $x$ variable increases? (p. 190)

4.1.7

They decrease.

Question 4.8

8. Suppose that the correlation coefficient $r$ equals 0. Does this mean that $x$ and $y$ have no relationship? Explain. (pp. 192, 197)

PRACTICING THE TECHNIQUES

CHECK IT OUT!

To do	Check out	Topic
Exercises 9–12	Example 1	Predictor variables and response variables
Exercises 13a–20a	Example 2	Constructing a scatterplot
Exercises 13b–20b and 21–26	Example 3	Describing the relationship between $x and y$
Exercises 13c–20c and 31–34	Example 4	Calculating the correlation coefficient $r$
Exercises 13d–20d and 27–30	Example 5	Interpreting the correlation coefficient $r$

Page 201

For Exercises 9–12, two variables are given. Determine which variable is the predictor variable $(x)$ and which is the response variable $(y)$ .

Question 4.9

9. The heights (in inches) and weights (in pounds) of a sample of five women are recorded.

4.1.9

Predictor ( $x$ ): Height

Response ( $y$ ): Weight

Question 4.10

10. The number of days absent from a class, and the course grade.

Question 4.11

11. The cost of a repair job and the number of hours spent on the repair.

4.1.11

Predictor ( $x$ ): The number of hours spent on the repair

Response ( $y$ ): The cost of a repair job

Question 4.12

12. Attendance at a baseball game (in thousands), and the amount of rainfall at a baseball stadium that day (in inches).

For Exercises 13–20, do the following for the indicated data set:

Construct a scatterplot of the relationship between $x$ and $y$ .
Interpret the scatterplot.
Calculate the correlation coefficient $r$ .
Interpret the value of the correlation coefficient $r$ .

Question 4.13

13. The values of $x$ and $y$ are as follows:

$x$	$y$
10	2
20	2
30	3
40	4
50	4

4.1.13

(a)

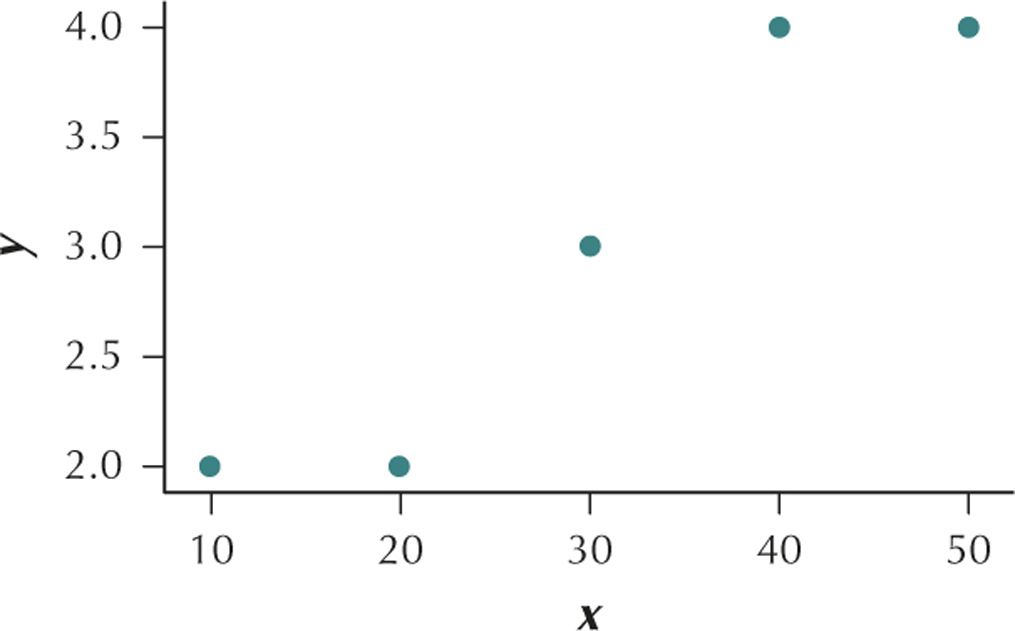
(b) The variables $x$ and $y$ have a positive linear relationship. (c) $r = 0.9487$ (d) This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that $x$ and $y$ are positively correlated. As $x$ increases, $y$ also tends to increase.

Question 4.14

14. The values of $x$ and $y$ are given as follows:

$x$	$y$
1	10
2	9
3	8
4	8
5	7

Question 4.15

15. The predictor variable $(x)$ and the response variable $(y)$ take the following values:

$x$	$y$
−5	−5
−5	−15
0	−20
5	−25
5	−30

4.1.15

(a)

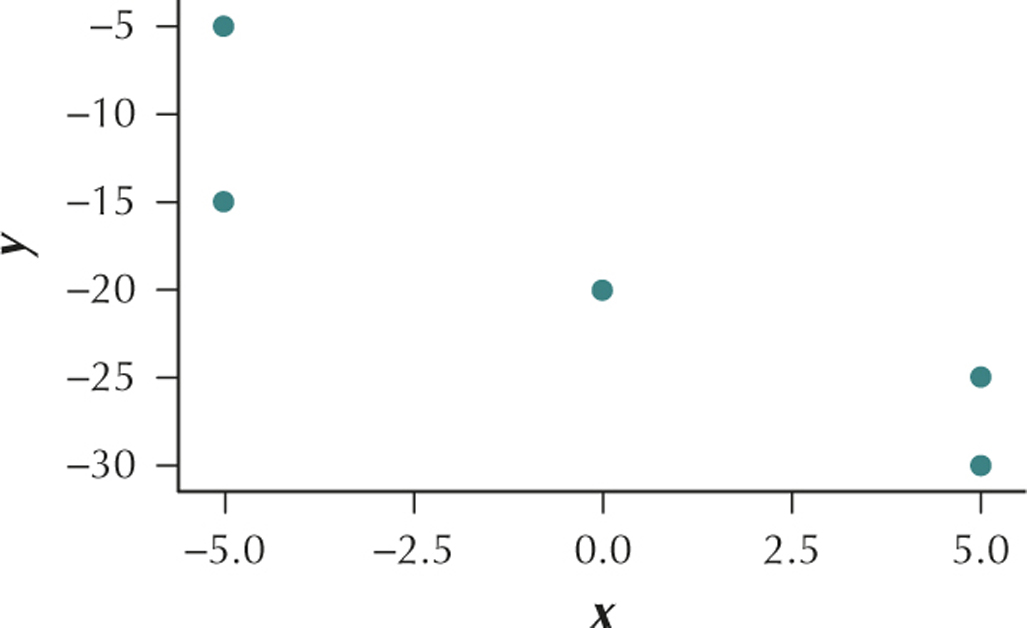
(b) The variables $x$ and $y$ have a negative linear relationship. (c) $r = - 0.9098$ (d) This value of $r$ is very close to the minimum value $r = - 1$ . We would therefore say that $x$ and $y$ are negatively correlated. As $x$ increases, $y$ tends to decrease.

Question 4.16

16. The predictor variable $(x)$ and the response variable $(y)$ take the following values:

$x$	$y$
0	10
20	10
40	15
60	20
80	20

Question 4.17

17. The heights (in inches) and weights (in pounds) of a sample of five women are recorded:

Height	Weight
66	122
67	133
69	153
68	138
65	125

4.1.17

(a)

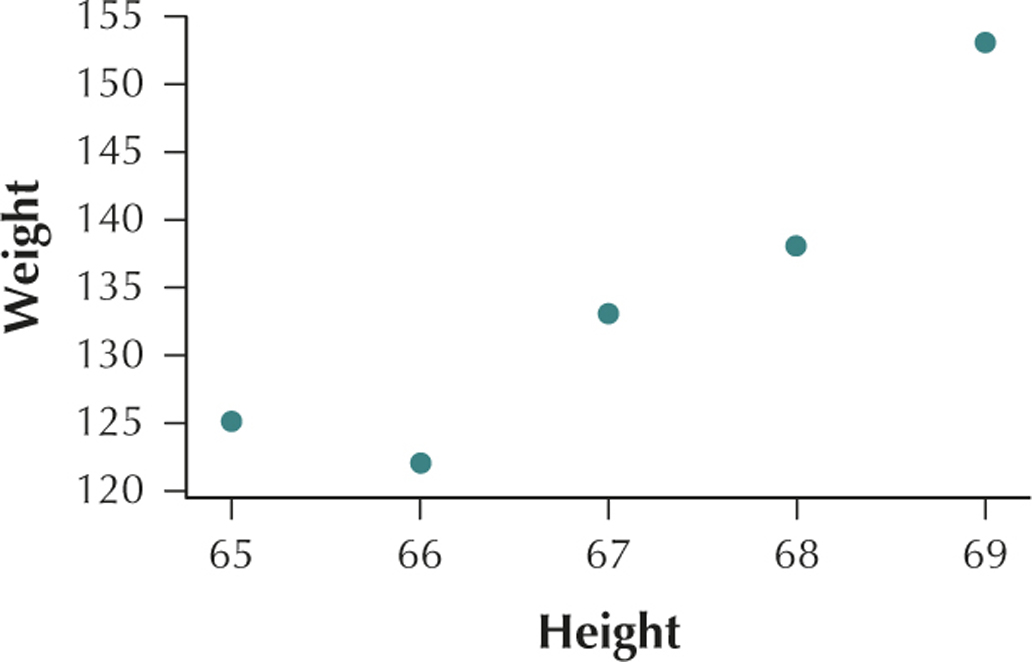
(b) The variables height and weight have a positive linear relationship. (c) $r = 0.9274$ (d) This value of $r$ is very close to the maximum value $r = 1$ .

We would therefore say that height and weight are positively correlated. As height increases, weight also tends to increase.

Question 4.18

18. The number of days absent from a class, and the course grade:

Days absent	Course grade
0	95
2	90
4	85
6	70
8	60

Question 4.19

19. The cost of a repair job, and the number of hours spent on the repair:

Cost	Hours
120	2
180	3
230	5
350	8
380	10

4.1.19

(a)

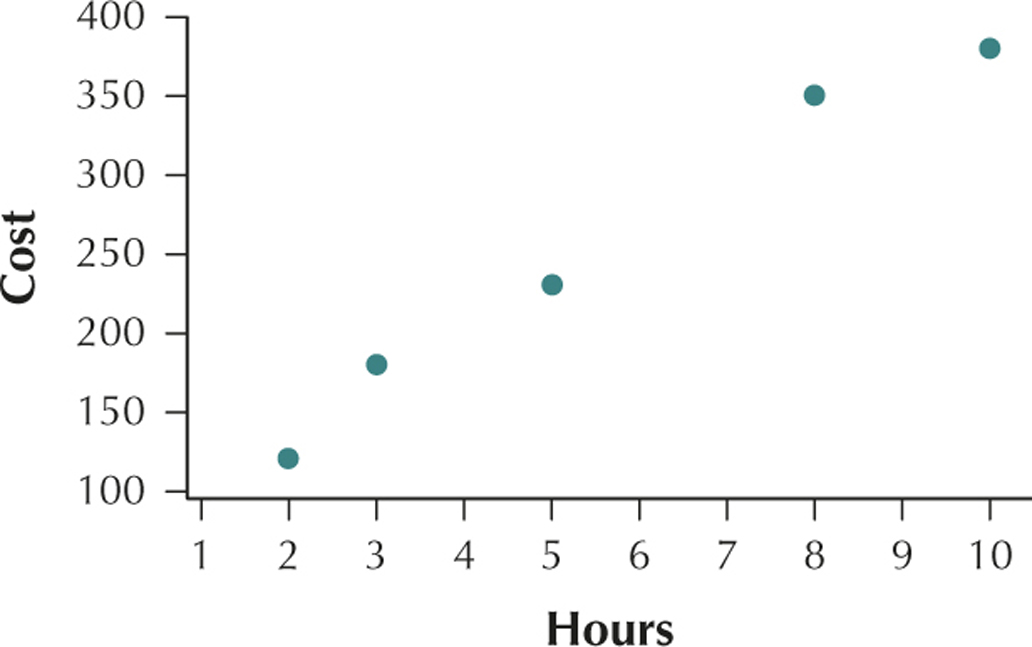
(b) The hours a repair job takes and the cost of the repair job have a positive linear relationship. (c) $r = 0.9896$ (d) This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that hours worked and cost are positively correlated. As the number of hours worked increases, the cost also tends to increase.

Question 4.20

20. Attendance at a baseball game (in thousands), and the amount of rainfall at a baseball stadium that day (in inches):

Rain	Attendance
0.0	40
0.0	42
0.1	38
0.5	30
1.0	20

For Exercises 21–26, do the following:

Characterize the relationship between $x$ and $y$ .
State what happens to the values of the $y$ variable as the $x$ -values increase.

Question 4.21

21.

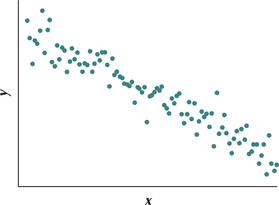
4.1.21

(a) Strong negative linear relationship (b) They decrease.

Page 202

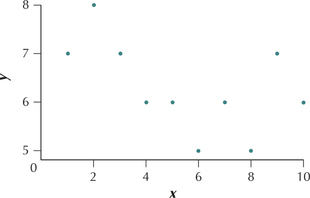
Question 4.22

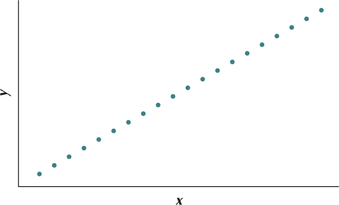
22.

Question 4.23

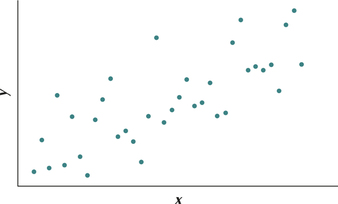
23.

4.1.23

(a) Moderate positive linear relationship (b) They increase.

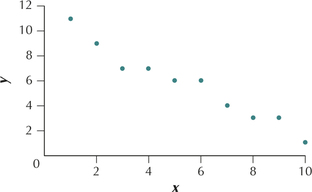
Question 4.24

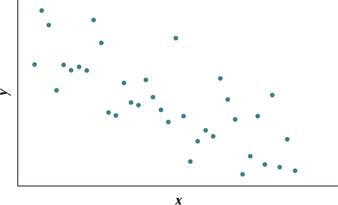
24.

Question 4.25

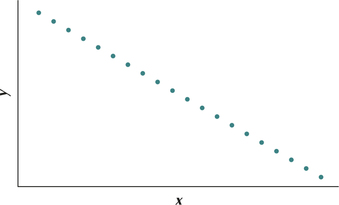
25.

4.1.25

(a) Perfect negative linear relationship (b) They decrease.

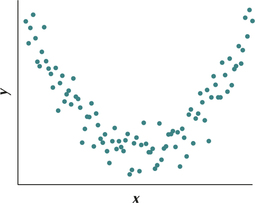
Question 4.26

26.

For Exercises 27–30, identify which of the scatterplots in i–iv represents the data set with the following correlation coefficients:

Question 4.27

27. Near 1

4.1.27

Question 4.28

28. Near zero

Question 4.29

29. Near −0.5

4.1.29

iii

Question 4.30

30. Near −1

In Exercises 31–34, the values for $x$ and $y$ in each scatterplot are integer-valued. For each scatterplot, (a) reconstruct the original data set, and (b) calculate the correlation coefficient for the data.

Question 4.31

31. The data in scatterplot i

4.1.31

(a) (1,1), (2,3), (3,3), (4,4), (5,6), (6,6), (7,7), (8,7), (9,9), (10,11)

(b) Minitab: Pearson correlation of $x$ and $y = 0.978$ . TI-83/84: $r = 0.9781316853$

Question 4.32

32. The data in scatterplot ii

Question 4.33

33. The data in scatterplot iii

4.1.33

(a) (1,7), (2,8), (3,7), (4,6), (5,6), (6,5), (7,6), (8,5), (9,7), (10,6) (b) Minitab: Pearson correlation of $x$ and $y = - 0.522$ . TI-83/84: $r = - 0.5222329679$

Question 4.34

34. The data in scatterplot iv

Page 203

APPLYING THE CONCEPTS

For Exercises 35–49, do the following:

Construct a scatterplot of the relationship between $x$ and $y$ .
Interpret the scatterplot.
Calculate the correlation coefficient $r$ .
Interpret the value of the correlation coefficient $r$ .

Question 4.35

videogamereg

35. Video Game Sales. The Chapter 1 Case Study looked at video game sales for the top 30 video games. The following table contains the weeks on the top 30 list $(x)$ and the total sales ( $y$ , in millions of game units).

Video game	Weeks $(x)$	Total sales in millions of units $(y)$
Super Mario Bros. U for WiiU	78	1.7
NBA 2K14 for PS4	27	0.6
Battlefield 4 for PS3	29	0.9
Titanfall for Xbox One	10	1.2
Yoshi's New Island for 3DS	10	0.2

Table 4.15: Source: www.vgchartz.com.

4.1.35

(a)

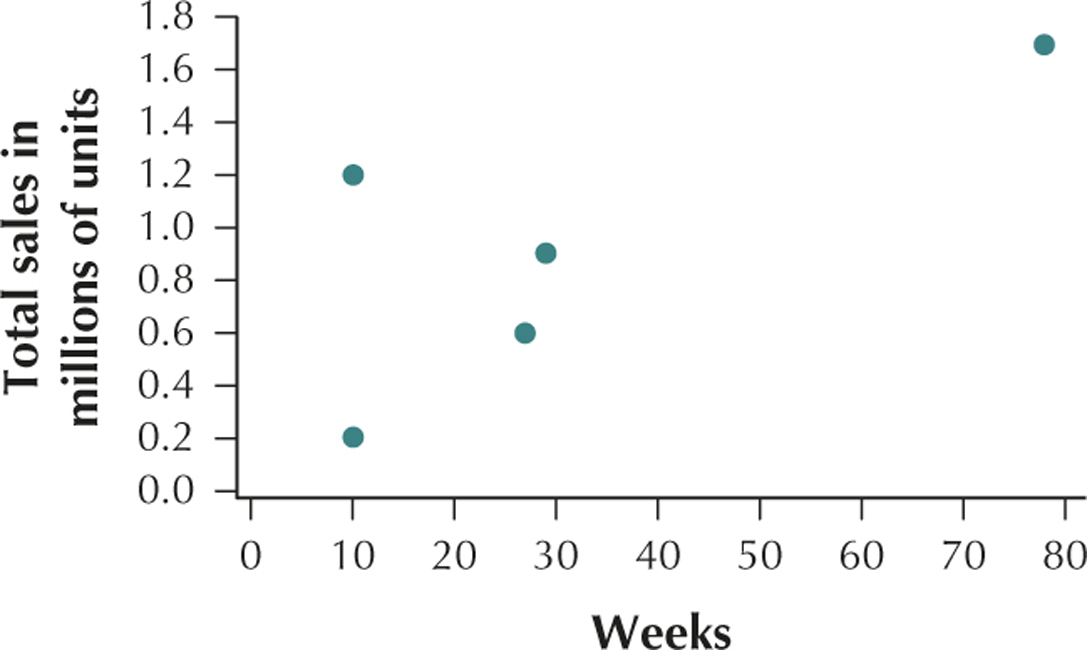
(b) The number of weeks on the top 30 list and the total sales in millions of game units have a positive linear relationship. (c) $r = 0.7403$ (d) This value of $r$ is close to the maximum value $r = 1$ . We would therefore say that weeks and total sales are positively correlated. As the number of weeks on the top 30 lists increases, the total sales also tends to increase.

Question 4.36

edunemploy

36. Does It Pay to Stay in School? The U.S. Census Bureau reported the following unemployment rates $(y)$ associated with the given years of education $(x)$ .

$x = years of education$	$y = unemployment rate$
5.0	16.8
7.5	17.1
8.0	15.3
10.0	20.6
12.0	11.7
14.0	8.1
16.0	3.8

Question 4.37

dartsdjia

37. Darts and the Dow Jones. The following table contains a random sample of eight days from the Chapter 3 Case Study data set, indicating the stock market gain or loss for the portfolio chosen by the random darts $(y)$ , as well as the Dow Jones Industrial Average (DJIA) gain or loss for that day $(x)$ .

Darts $(y)$	DJIA $(x)$
−27.4	−12.8
18.7	9.3
42.2	8.0
−16.3	−8.5
11.2	15.8
28.5	10.6
1.8	11.5
16.9	−5.3

Table 4.17: Source: The Wall Street Journal.

4.1.37

(a)

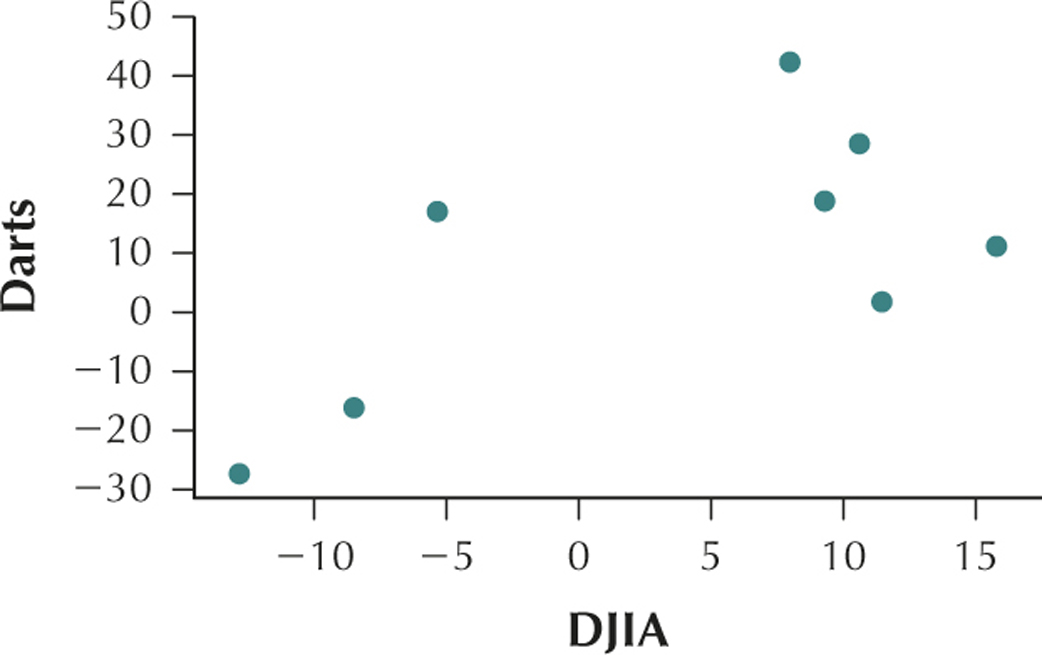
(b) The change in price of the stocks in the DJIA and the change in price of the stocks in the portfolio selected by the darts have a positive linear relationship. (c) $r = 0.6639$ (d) This value of $r$ is close to the maximum value $r = 1$ . We would therefore say that DJIA and Darts are positively correlated. As the change in stock prices of the stocks in the DJIA increases, the change in stock prices selected by darts also tends to increase.

Question 4.38

ageheight

38. Age and Height. The following table provides a random sample from the Chapter 4 Case Study data set body_females, showing the age $(x)$ and height $(y)$ of eight women.

Age $(x)$	Height $(y)$
40	63.5
28	63.0
25	64.4
34	63.0
26	63.8
21	68.0
19	61.8
24	69.0

Table 4.18: Source: Journal of Statistics Education.

Question 4.39

gardasilreg

39. Gardasil Shots and Age. The accompanying table shows a random sample of 10 patients from the Chapter 5 Case Study data set, Gardasil, including the age of the patient $(x)$ and the number of shots taken by the patient $(y)$ .

Age $(x)$	Shots $(y)$
13	3
21	3
16	3
17	2
17	3
18	1
25	2
15	3
12	1
16	1

Table 4.19: Source: Journal of Statistics Education.

4.1.39

(a)

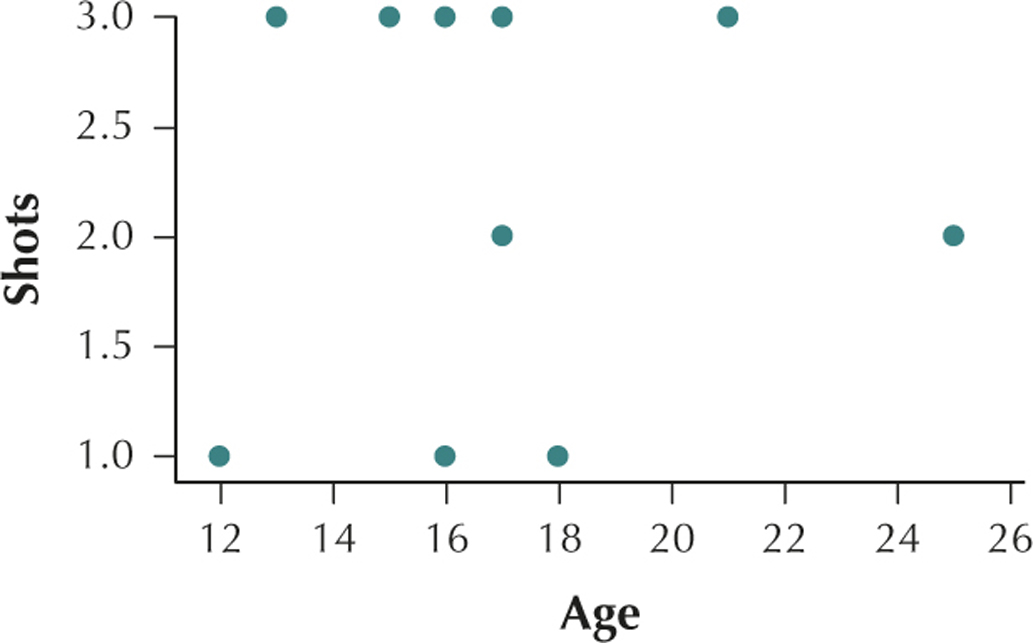
(b) Age and number of shots have no apparent relationship. (c) $r = 0.0641$ (d) This value of $r$ is very close to the value $r = 0$ . We would therefore say that there is no linear relationship between age and shots.

Question 4.40

ncaa2014

40. NCAA Power Ratings. The accompanying table shows the top 10 teams' winning percentages $(x)$ and power ratings $(y)$ for the 2013–2014 NCAA basketball season, according to www.teamrankings.com.

Page 204

Team	Winning proportion $(x)$	Power rating $(y)$
Florida	0.923	121.2
Wichita State	0.971	119.1
Arizona	0.868	118.8
Louisville	0.838	117.9
Connecticut	0.800	117.2
Virginia	0.811	116.8
Wisconsin	0.789	116.6
Villanova	0.853	116.4
Michigan State	0.763	115.9
Michigan	0.757	115.9

Question 4.41

satfatcorr

41. Saturated Fat and Calories. The table contains the calories and saturated fat in a sample of 10 food items.

Food item	Calories	Grams of saturated fat
Chocolate bar (1.45 ounces)	216	7.0
Meat & veggie pizza (large slice)	364	5.6
New England clam chowder (1 cup)	149	1.9
Baked chicken drumstick (no skin, medium size)	75	0.6
Curly fries, deep-fried (4 ounces)	276	3.2
Wheat bagel (large)	375	0.3
Chicken curry (1 cup)	146	1.6
Cake doughnut hole (one)	59	0.5
Rye bread (1 slice)	67	0.2
Raisin bran cereal (1 cup)	195	0.3

Table 4.21: Source: Food-a-Pedia.

4.1.41

(a)

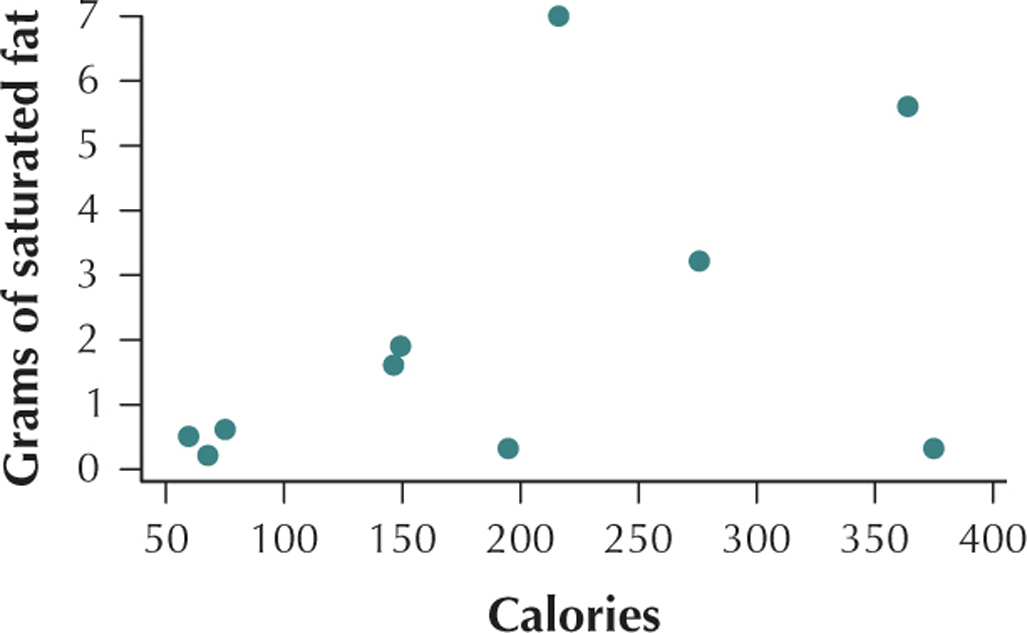
(b) The number of calories in a serving of food and the grams of saturated fat in a serving of food have a positive linear relationship. (c) $r = 0.4482$ (d) This value of $r$ is positive. We would therefore say that the number of calories in a serving of food and the grams of saturated fat in a serving of food are positively correlated. As the number of calories in a serving of food increases, the grams of saturated fat in a serving of food also tends to increase.

Question 4.42

displacement

42. Engine Displacement and Gas Mileage. The table provides the engine displacement (size, in liters) and the city mpg (miles per gallon) gas mileage of a random sample of 12 vehicles taken from the Chapter 6 Case Study data set, FuelEfficiency.

Vehicle	Engine displacement	City mpg
GMC Yukon Denali	6.2	13
Ford E350 Wagon	5.4	11
BMW435i Coupe	3.0	20
Land Rover Range Rover	5.0	13
Infiniti Q50a	3.7	19
Dodge Journey	3.6	17
Jaguar XF	5.0	15
Dodge Challenger	6.4	14
Toyota Highlander Hybrid	3.5	28
Mercedes-Benz S550	4.7	17
Ford Fiesta	1.6	29
Hyundai Elantra	2.0	24

Question 4.43

collegecompleters

43. Completing College. The twenty-first century economy not only needs students to attend college; it needs students to complete their college degrees, in order to compete in the information age. The table contains a sample of 10 states, with data on the percentage of residents who have attended college $(x)$ and the percentage of college attendees who have completed their college degrees $(y)$ .

State	$x = college attenders$	$y = college completers$
California	30.9	38.8
Florida	26.6	35.5
Georgia	30.1	34.1
Illinois	35.7	39.1
Massachusetts	45.2	45.9
New York	38.7	42.8
North Carolina	30.1	35.5
Ohio	28.4	37.1
Pennsylvania	32.5	40.2
Texas	26.2	32.2

Table 4.23: Source: American Community Survey.

4.1.43

(a)

(b) The percent of residents of a state who attend college and the percent of residents of a state who graduate from college have a positive linear relationship. (c) $r = 0.9196$ (d) This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that college attenders and college completers are positively correlated. As the number of college attenders increases, the number of college completers also tends to increase.

Question 4.44

walkbike

44. Walking or Biking to Work. In these days of high gas prices, it is worth considering alternative methods of commuting. The table contains, for a sample of 10 American cities, the percentage of people who walk to work $(x)$ and the percentage of people who bike to work $(y)$ .

City	$x = walk to work$	$y = bike to work$
Anaheim	1.8	0.9
Baltimore	6.5	0.8
Buffalo	6.2	0.9
Cincinnati	5.4	0.5
Detroit	3.1	0.3
Jacksonville	1.4	0.4
Las Vegas	1.9	0.4
New Orleans	5.1	2.1
Orlando	1.9	0.4
Sacramento	3.2	2.5

Table 4.24: Source: U.S. Census Bureau.

Question 4.45

teenbirth

45. Teenage Birth Rate. The National Center for Health Statistics publishes data on state birth rates. The table contains the overall birth rate and the teenage birth rate for eight randomly chosen states. The overall birth rate is defined by the NCHS as “live births per 1000 women,” and the teenage birth rate is defined as “live births per 1000 women aged 15–19.”

Page 205

State	$x = overall birth rate$	$y = teen birth rate$
California	62.0	23.6
Florida	59.3	24.6
Georgia	61.6	30.5
New York	58.8	17.7
Ohio	62.7	27.2
Pennsylvania	58.4	20.9
Texas	69.9	41.0
Virginia	60.9	20.1

4.1.45

(a)

(b) The overall birth rate and the teenage birth rate have a positive linear relationship. (c) $r = 0.9059$ (d) This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that overall birth rate and teen birth rate are positively correlated. As the overall birth rate increases, the teen birth rate also tends to increase.

Question 4.46

brainbody

46. Brain and Body Weight. A study compared the body weight (in kilograms) and brain weight (in grams) for a sample of mammals, with the results shown in the following table.²

$x = body weight (kg)$	$y = brain weight (g)$
52.16	440.0
60.00	81.0
27.66	115.0
85.00	325.0
36.33	119.5
100.00	157.0
35.00	56.0
62.00	132.0
83.00	98.2
55.50	175.0

Question 4.47

consumersentiment

47. Consumer Sentiment. Would you expect the consumer sentiment (a measure of how upbeat a consumer feels about his or her personal economic condition) of those with lower incomes to be correlated with that of those with higher incomes, over time? The University of Michigan's Survey of Consumers published the data in the following table, showing the consumer sentiment in 2013 month by month for the two groups.

Month	$x = consumer sentiment for incomes under $75,000$	$y = consumer sentiment for incomes $75,000 or higher$
Jan	71.6	80.2
Feb	75.7	82.4
Mar	78.3	83.7
Apr	74.5	79.8
May	80.3	94.1
Jun	76.1	98.9
Jul	82.4	90.0
Aug	78.0	89.6
Sep	72.3	86.2
Oct	71.4	77.0
Nov	67.9	88.7
Dec	78.9	88.0

4.1.47

(a)

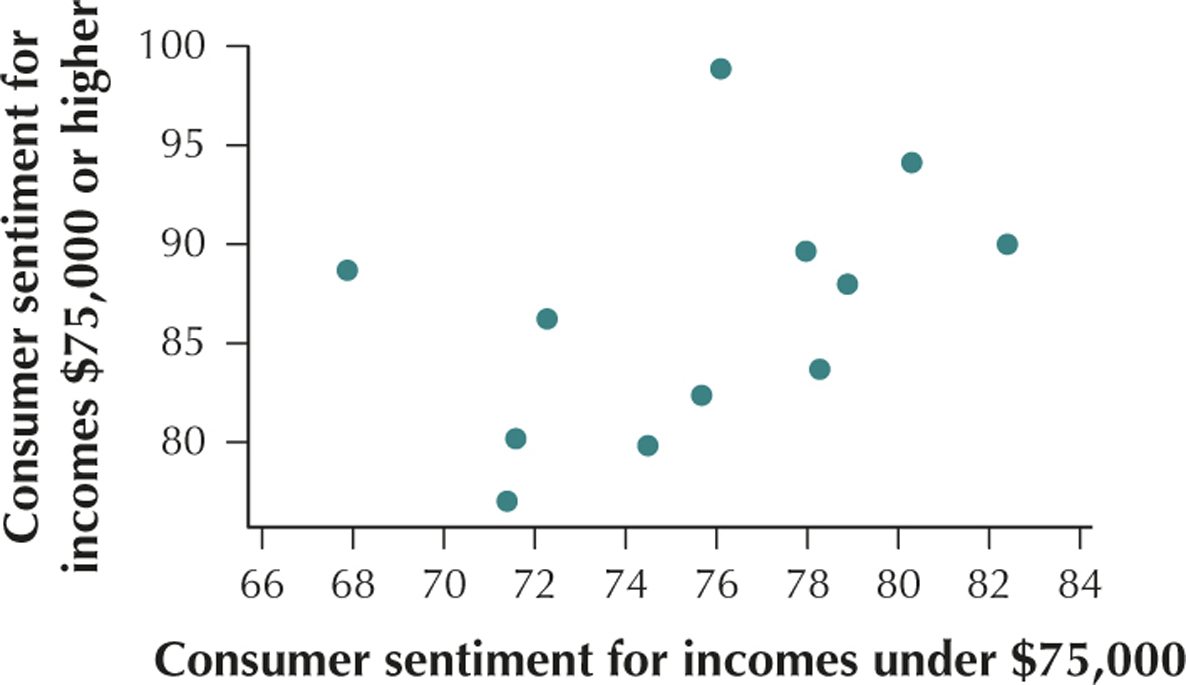
(b) The consumer sentiment for incomes under $75,000 and the consumer sentiment for incomes $75,000 or higher have a positive linear relationship. (c) $r = 0.4296$ (d) This value of $r$ is positive. We would therefore say that the consumer sentiment for incomes under $75,000 and the consumer sentiment for incomes $75,000 or higher are positively correlated. As the consumer sentiment for incomes under $75,000 increases, the consumer sentiment for incomes $75,000 or higher also tends to increase.

Question 4.48

satlanguages

48. SAT Scores, by Foreign Language. The table contains the mean 2014 SAT Critical Reading and Math scores, which are categorized by the foreign language taken in high school or spoken at home.

Language	SAT Critical Reading score	SAT Mathematics score
Chinese	535	606
French	519	525
German	530	540
Greek	526	543
Hebrew	526	541
Italian	497	509
Japanese	521	552
Korean	490	576
Latin	556	556
Russian	483	535
Spanish	498	508

Question 4.49

batters2014

49. Batting Average and Runs Scored. The table shows the top 10 hitters in the American League of Major League Baseball for 2014. We are interested in estimating the number of runs scored $(y)$ using the player's batting average $(x)$ .

Batter	Team	Runs scored	Batting average
Jose Altuve	Houston Astros	85	0.341
Victor Martinez	Detroit Tigers	87	0.335
Michael Brantley	Cleveland Indians	94	0.327
Adrian Beltre	Texas Rangers	79	0.324
Jose Abreu	Chicago White Sox	80	0.317
Robinson Cano	Seattle Mariners	77	0.314
Miguel Cabrera	Detroit Tigers	101	0.313
Melky Cabrera	Toronto Blue Jays	81	0.301
Adam Eaton	Chicago White Sox	76	0.300
Howie Kendrick	Los Angeles Angels	85	0.293

4.1.49

(a)

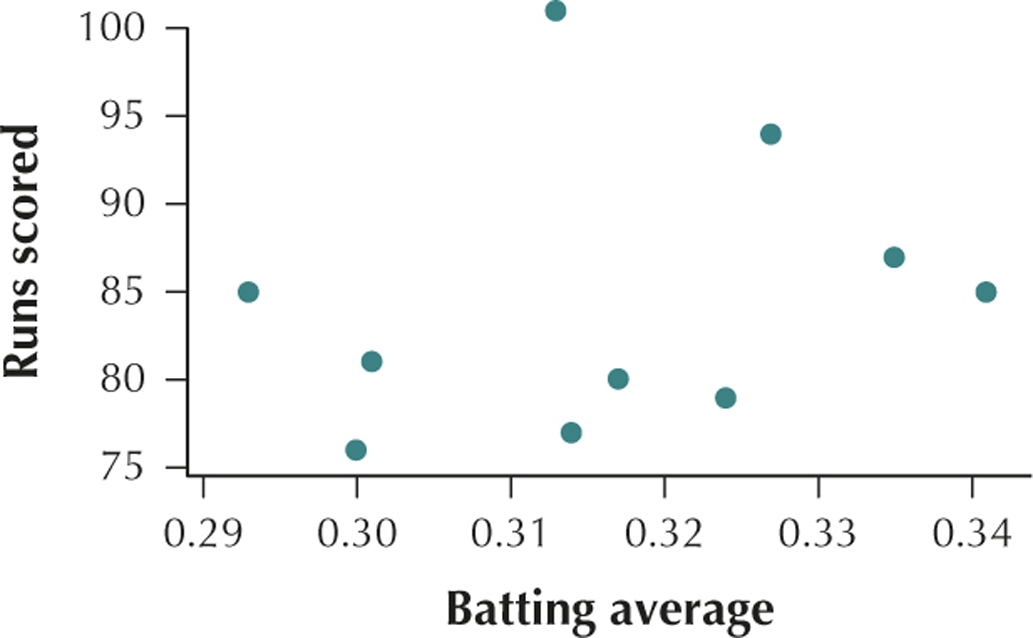
(b) The batting average of a baseball player and the number of runs scored by a baseball player have no apparent relationship. (c) $r = 0.2332$ (d) This value of $r$ is very close to the value $r = 0$ . We would therefore say that there is no linear relationship between batting average and runs scored.

Correlation in Accounting. A company's current ratio measures its ability to pay its short-term obligations. Use the data in the table, which contains a random sample of large technology companies in 2010, for Exercises 50–56. Total assets and total liabilities are in billions of dollars.

Page 206

Company	Current ratio	Price- earnings ratio	Assets	Liabilities
Microsoft	1.82	12.51	77.9	38.3
Intel	2.79	18.44	53.1	11.4
Dell	1.28	10.95	33.7	28.0
Apple	1.88	24.57	53.9	26.0
Google	10.62	18.87	40.5	4.5

Table 4.30: Source: Lexis Nexis.

Question 4.50

accountingcorr

50. Provide and interpret a scatterplot of liabilities versus assets.

Question 4.51

accountingcorr

51. Calculate and interpret the correlation coefficient between liabilities and assets.

4.1.51

$r = 0.5554$ ; This value of $r$ is positive. We would therefore say that assets and liabilities are positively correlated. As assets increase, liabilities also tend to increase.

Question 4.52

accountingcorr

52. Provide and interpret a scatterplot of current ratio versus price-earnings ratio.

Question 4.53

accountingcorr

53. Calculate and interpret the correlation coefficient between current ratio and price-earnings ratio.

4.1.53

$r = 0.2443$ ; This value of $r$ is very close to the value $r = 0$ . We would therefore say that there is no linear relationship between price–earnings ratio and current ratio.

Question 4.54

accountingcorr

54. Compute a new variable, called net worth, which equals assets – liabilities.

Question 4.55

accountingcorr

55. Provide and interpret a scatterplot of net worth versus current ratio.

4.1.55

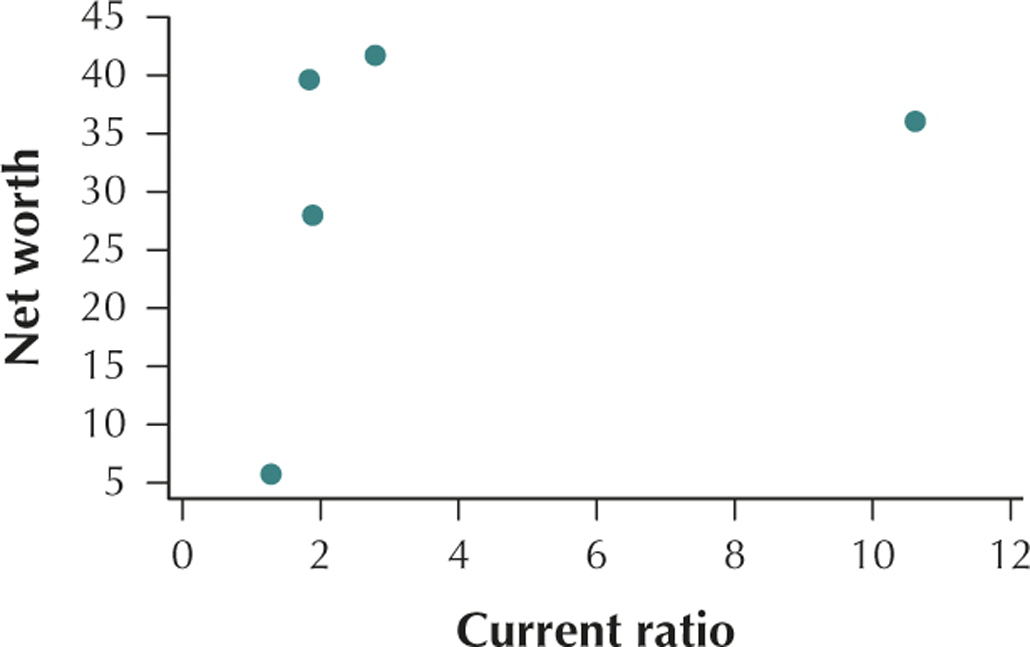
The current ratio of a company and the company's net worth have a positive linear relationship.

Question 4.56

accountingcorr

56. Calculate and interpret the correlation coefficient between net worth and current ratio.

Best Places for Dating. Sperling's Best Places published the list of best places for dating in America. The table shows the top 10 places, along with the overall dating score $(y)$ and a set of predictor variables. Use this information for Exercises 57–59.

City	$y = overall dating score$	Percentage 18–24 years old	Percentage 18–24 who are single	Online dating score
Austin	100.0	13.4%	81.2%	77.8
Colorado Springs	88.7	10.5%	74.2%	88.9
San Diego	84.0	11.3%	79.4%	77.4
Raleigh	80.7	11.6%	82.9%	79.2
Seattle	78.7	9.0%	83.9%	100.0
Charleston	78.7	11.2%	82.7%	66.9
Norfolk	77.0	11.2%	75.6%	82.9
Ann Arbor	75.5	12.9%	90.3%	51.1
Springfield	75.2	11.7%	89.8%	63.5
Honolulu	75.2	10.1%	82.3%	50.2

Question 4.57

bestdating

57. Construct and interpret a scatterplot for each of the following predictor variables versus the overall dating score:

Percentage 18–24 years old
Percentage 18–24 years old who are single
Online dating score

4.1.57

(a)

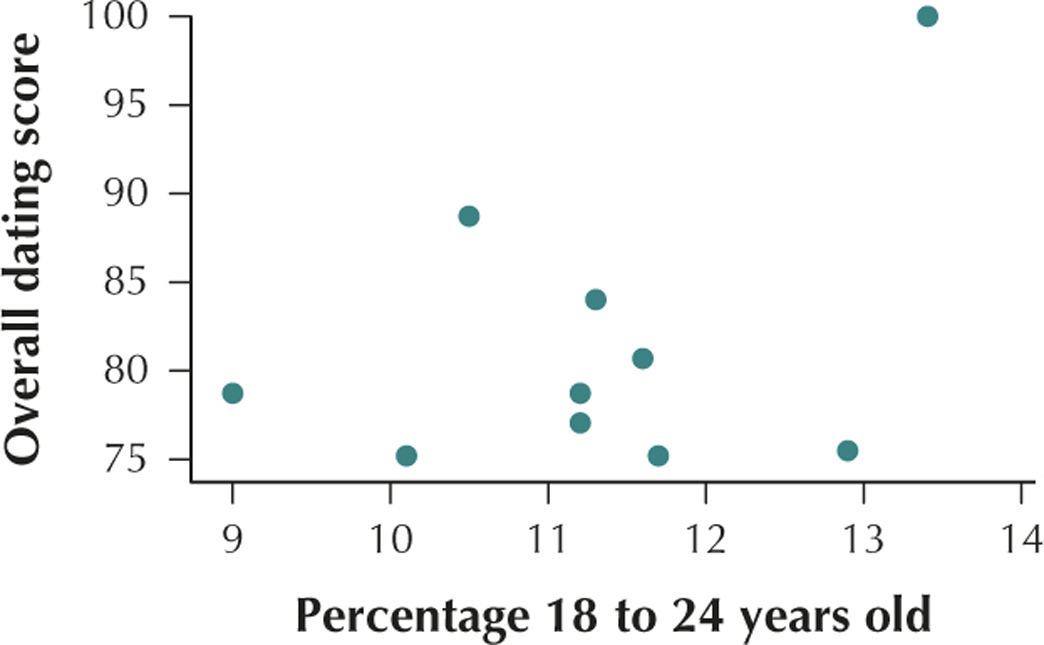
The percentage of 18- to 24-year-olds in a city and the overall dating score in a city have a positive linear relationship.

(b)

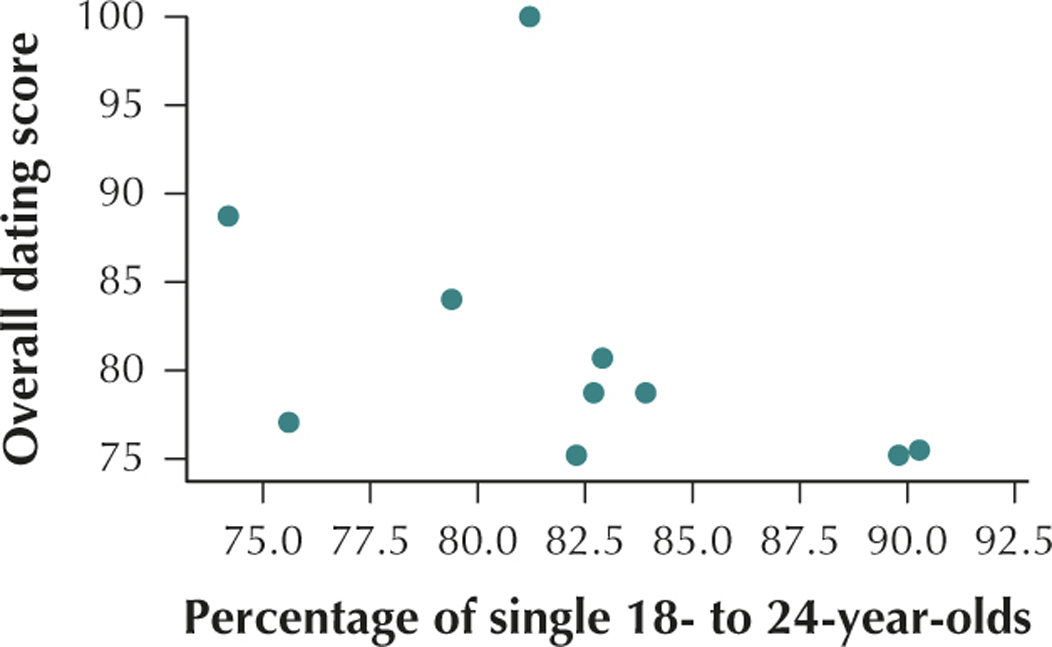
The percentage of a city's residents who are 18- to 24-year-olds and single and the overall dating score of a city have a negative linear relationship.

(c)

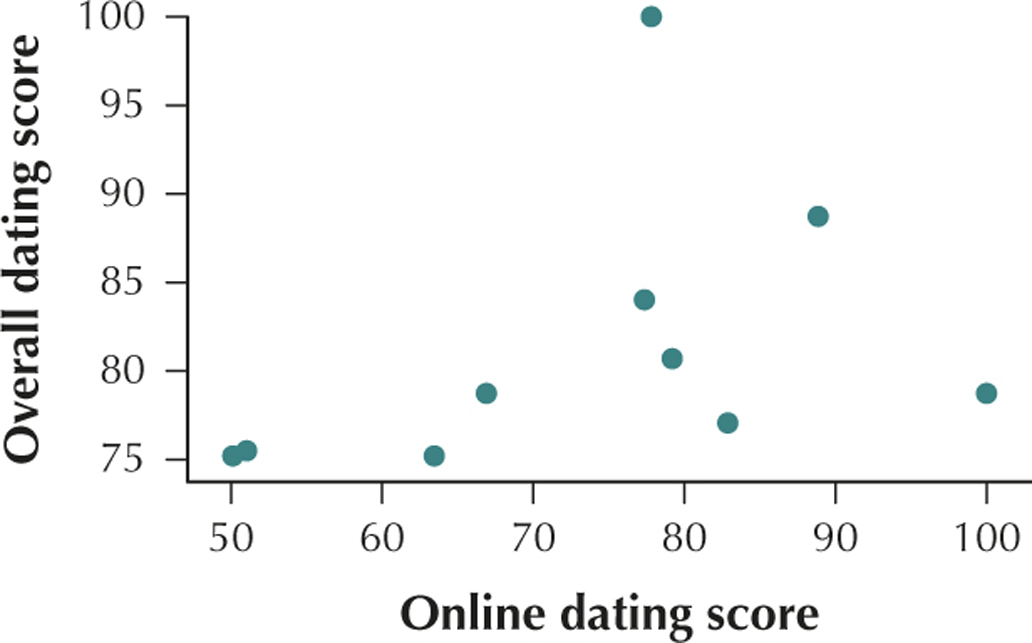
The online dating score of a city and the overall dating score of a city have a positive linear relationship.

Question 4.58

bestdating

58. Calculate and interpret the correlation coefficient $r$ between each of the following predictor variables and the overall dating score:

Percentage 18–24 years old
Percentage 18–24 years old who are single
Online dating score

Question 4.59

bestdating

59. Based on your work in Exercises 57 and 58, which predictor variable is the best indicator of the overall dating score, and thus an indicator of the best places for dating?

4.1.59

Percentage of 18- to 24-year-olds who are single

Virginia Weather. The table contains data on weather in a sample of cities in the state of Virginia. Use this information for Exercises 60–65.

Data on the weather in Virginia
City	Average January temperature	Heating degree- days	Average July temperature	Cooling degree- days
Alexandria	34.9	4055	79.2	1531
Arlington	34.9	4055	79.2	1531
Blacksburg	30.9	5559	71.1	533
Charlottesville	35.5	4103	76.9	1212
Chesapeake	40.1	3368	79.1	1612
Danville	36.6	3970	78.8	1418
Hampton	39.4	3535	78.5	1432
Harrisonburg	30.5	5333	73.5	758
Leesburg	31.5	5031	75.2	911
Lynchburg	34.5	4354	75.1	1075
Manassas	31.7	4925	75.7	1075
Newport News	41.2	3179	80.3	1682
Norfolk	40.1	3368	79.1	1612
Petersburg	39.7	3334	79.6	1619
Portsmouth	40.1	3368	79.1	1612
Richmond	36.4	3919	77.9	1435
Roanoke	35.8	4284	76.2	1134
Suffolk	39.6	3467	78.5	1427
Virginia Beach	40.7	3336	78.8	1482

Table 4.32: Source: National Oceanic and Atmospheric Administration.

Question 4.60

vaweather

60. Construct and interpret a scatterplot for the average January temperature versus the cooling degree-days.

Question 4.61

vaweather

61. Based on your scatterplot, what would you expect the sign of the correlation coefficient to be? Why?

4.1.61

Positive. The scatterplot indicates a positive linear relationship between cooling-degree days and the average January temperature.

Question 4.62

vaweather

62. Calculate the correlation coefficient $r$ between the average January temperature and the cooling degree-days.

Question 4.63

vaweather

63. Build and interpret a scatterplot for the average July temperature versus the heating degree-days.

4.1.63

Heating degree-days and the average July temperature have a negative linear relationship.

Question 4.64

vaweather

64. Calculate the correlation coefficient $r$ between the average July temperature and the heating degree-days.

Question 4.65

vaweather

65. Which relationship would you say is stronger: the relationship between the average January temperatures with the cooling degree-days, or the relationship between the average July temperatures and the heating degree-days?

4.1.65

The relationship between the average July temperatures and the heating degree-days is stronger.

What's Your Major? The table contains the percentages of students majoring in (i) Mathematics/Statistics/Computer Science, (ii) Biological Sciences, and (iii) Psychology, for a sample of 10 states. Use this information for Exercises 66–71.

Page 207

State	Math/Stat/ Comp Sci	Biological Sci	Psychology
Alaska	2.0	11.0	5.5
Connecticut	4.1	5.3	5.7
Hawaii	2.9	6.9	5.2
Idaho	3.7	9.6	3.2
Maryland	5.7	7.1	4.8
Montana	2.7	11.1	4.1
New Jersey	5.3	5.3	4.7
Oregon	3.2	8.4	5.4
Virginia	5.5	5.4	4.7
Wyoming	2.2	12.2	3.6

Table 4.33: Source: American Community Survey.

Question 4.66

statemajors

66. Construct a scatterplot of the Math/Stat/Comp Sci majors versus the Psychology majors.

Question 4.67

statemajors

67. Based on your scatterplot, would you say that a relationship exists between the two sets of majors?

4.1.67

No.

Question 4.68

statemajors

68. Calculate the correlation coefficient $r$ between the Math/Stat/Comp Sci majors and the Psychology majors. Was your intuition in Exercise 67 confirmed?

Question 4.69

statemajors

69. Construct a scatterplot of the Biological Science majors versus the Psychology majors.

4.1.69

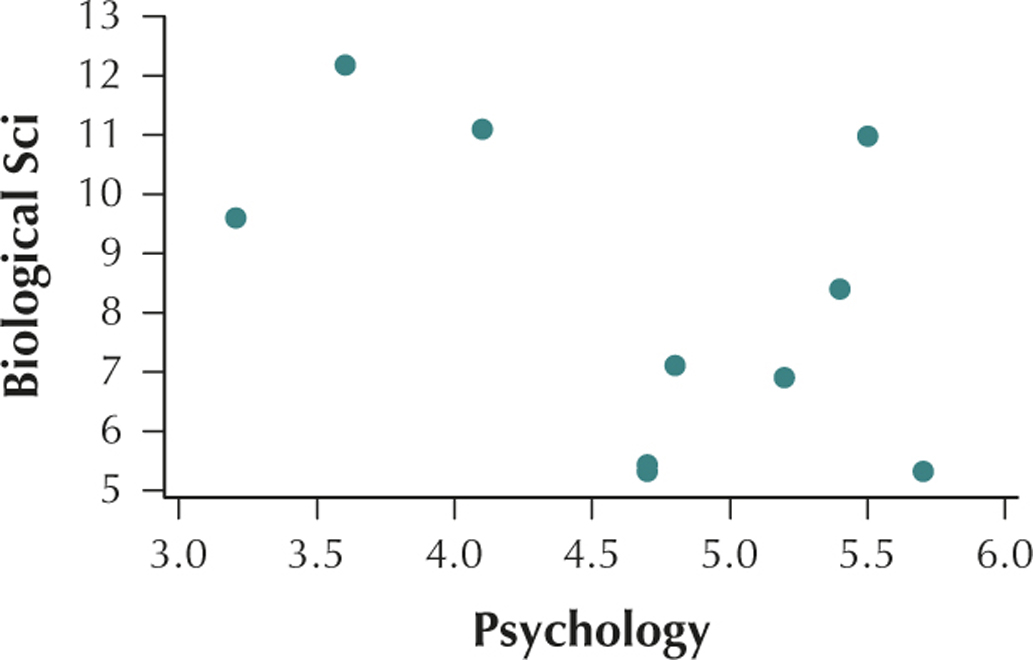
Question 4.70

statemajors

70. Based on your scatterplot in Exercise 69, would you say that a relationship exists between the two sets of majors?

Question 4.71

statemajors

71. Calculate the correlation coefficient $r$ between the Biological Science majors and the Psychology majors. Was your intuition in Exercise 70 confirmed?

4.1.71

$r = - 0. 4858$ . Yes.

Worldwide Indicators of Well-Being. The Statistics Online Computational Resource (SOCR) provides resources for statistics students and educators. The following table, sampled from data provided by SOCR, includes 10 countries, along with 3 indicators of their well-being: an indicator of economic dynamism, a measure of literacy, and a health indicator. Use this information for Exercises 72–82.

Country	Economy	Literacy	Health
Australia	71.5	91.5	95.2
Canada	68.5	96.7	92.8
Germany	61.9	91.1	92.8
India	50.0	66.2	51.7
Japan	69.0	94.0	100.0
Mexico	42.0	74.7	78.3
Pakistan	41.5	66.9	49.3
South Korea	73.0	96.7	87.9
United Kingdom	72.9	92.8	90.3
United States	77.8	89.4	85.5

Question 4.72

wellbeing

72. Some analysts claim that literacy depends on the economy of a country. Provide a scatterplot of literacy $(y)$ versus economy $(x)$ . Describe any relationship between the variables.

Question 4.73

wellbeing

73. Calculate and interpret the correlation coefficient $r$ for the linear relationship between $x = economy$ and $y = literacy$ .

4.1.73

$r = 0.8811$ . This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that economy and literacy are positively correlated. As the economy increases, literacy also tends to increase.

Question 4.74

wellbeing

74. Other analysts state that a country's economy depends on the country's literacy. Build a scatterplot of economy $(y)$ versus literacy $(x)$ . Describe any relationship between the variables. Compare this scatterplot with the one in Exercise 72. Discuss similarities and differences.

Question 4.75

wellbeing

75. Do you expect that the correlation coefficient between $x = economy$ and $y = literacy$ will be the same as that between $x = literacy$ and $y = economy$ ? Calculate and interpret the correlation coefficient $r$ for the linear relationship between $x = literacy$ and $y = economy$ . Was your intuition confirmed?

4.1.75

Yes. $r = 0.8811$ . Yes.

Question 4.76

wellbeing

76. Provide a scatterplot of literacy $(y)$ versus health $(x)$ . Describe any relationship between the variables.

Question 4.77

wellbeing

77. Calculate and interpret the correlation coefficient $r$ for the linear relationship between $x = health$ and $y = literacy$ .

4.1.77

$r = 0.9309$ . This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that health and literacy are positively correlated. As health increases, literacy also tends to increase.

Question 4.78

wellbeing

78. Without calculating it, state what the correlation coefficient $r$ would be for the linear relationship between $x = literacy$ and $y = health$ .

Question 4.79

wellbeing

79. Provide a scatterplot of health $(y)$ versus economy $(x)$ . Describe any relationship between the variables.

4.1.79

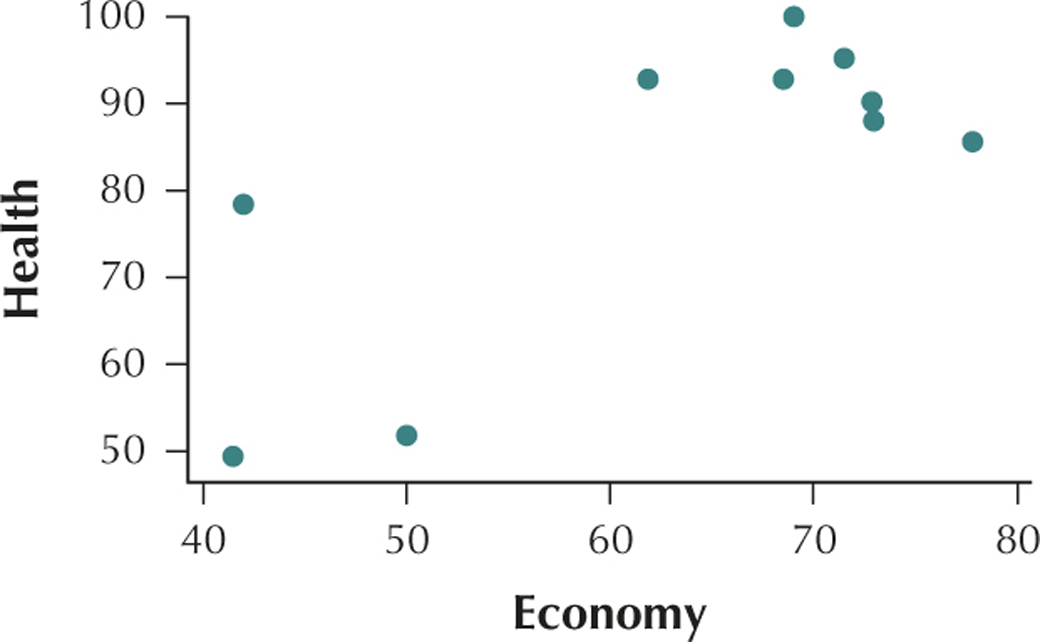
Economy and health have a positive linear relationship.

Question 4.80

wellbeing

80. Calculate and interpret the correlation coefficient $r$ for the linear relationship between $x = economy$ and $y = health$ .

Question 4.81

wellbeing

81. Without calculating it, state what the correlation coefficient $r$ would be for the linear relationship between $x = health$ and $y = economy$ .

4.1.81

$r = 0.7598$

Question 4.82

wellbeing

82. Based on your work in the previous exercises, state a general rule about the correlation between $x$ and $y$ , and the correlation between $y$ and $x$ .

Question 4.83

83. Computational Formula for $r$ . The following computational formula may be used as an equivalent of the definition formula for the correlation coefficient $r$ :

$r = \frac{\sum x y - (\sum x \sum y) / n}{(n - 1) s_{x} s_{y}}$

Use the computational formula and the TI-83/84 to calculate the correlation coefficient $r$ for the relationship between square footage and sales price of the eight home lots for sale in Glen Ellyn from Example 2 (page 189).

4.1.83

$r = 0.9434$

sqrfootsale

BRINGING IT ALL TOGETHER

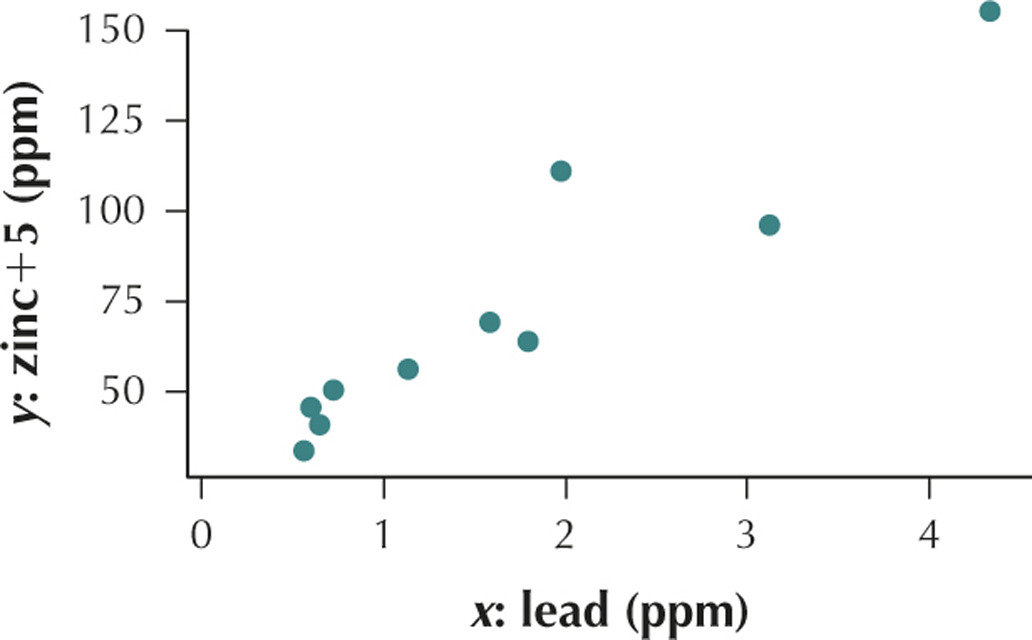
Lead and Zinc Concentrations in River Fish. Like to go fishing? In some areas, it may not be healthy to eat the fish you catch, due to the pollutants in the river that the fish ingest. Use the information in the table for Exercises 84–88. The table contains the lead and zinc concentrations in river fish from the Spokane River in Washington State, in parts per million.³

Page 208

Fish	$x : lead (ppm)$	$y : zinc (ppm)$
1	0.73	45.3
2	1.14	50.8
3	0.60	40.2
4	1.59	64.0
5	4.34	150.0
6	1.98	106.0
7	3.12	90.8
8	1.80	58.8
9	0.65	35.4
10	0.56	28.4

Question 4.84

leadzincfish

84. Investigate the relationship.

Construct a scatterplot of the variables. Make sure the $y$ variable goes on the y axis.
What type of relationship do these variables have: positive, negative, or no apparent linear relationship?
Will the correlation coefficient be positive, negative, or near zero?

Question 4.85

leadzincfish

85. Calculate and interpret the correlation coefficient.

Compute the value of the correlation coefficient.
Does this value for $r$ concur with your judgment in part (c) of the previous exercise?
Interpret the meaning of this value of the correlation coefficient.

4.1.85

(a) $r = 0.9405$ (b) Yes. (c) This value of $r$ is very close to the maximum value $r = 1$ . We would therefore say that lead and zinc are positively correlated. As the lead content in the fish increases, the zinc content in the fish also tends to increase.

Question 4.86

leadzincfish

86. Determine whether we can conclude that $x$ and $y$ are correlated.

Question 4.87

leadzincfish

87. Transformation. Add 5 to each value for $y$ .

Redraw the scatterplot. Comment on the similarity or difference from the scatterplot in Exercise 84(a).
Recalculate the correlation coefficient.
Compare your answers from Exercises 85(a) and 87(b).
Compose a rule that states the behavior of the correlation coefficient $r$ when a constant is added to each $y$ data value.

4.1.87

(a)

Everything is the same except the dots are shifted up 5 ppm. (b) $r = 0.9405$ (c) They are the same. (d) When a constant is added to each $y$ -data value the correlation coefficient stays the same.

Question 4.88

leadzincfish

88. Transformation. What if, starting with the original data in the table, we added a certain unknown constant amount to each value for $x$ ?

Without redrawing the scatterplot, describe how this change would affect the scatterplot you drew in Exercise 84(a).
Without recalculating the correlation coefficient, state what you think the effect of this change would be on the correlation coefficient. Why do you think that?
Compose a rule that states the behavior of the correlation coefficient $r$ when a constant is added to each $x$ data value.

CONSTRUCT YOUR OWN DATA SETS

Question 4.89

89. Describe two variables from real life that would have a value of $r$ close to 1. Explain why they are positively correlated.

4.1.89

Answers will vary.

Question 4.90

90. Create a sample of five observations from each of your variables in the previous exercise, and put them into a table similar to Table 4 (page 194). Next, construct a scatterplot of the variables. Finally, draw a single straight line through the data points in the plot in a manner that you think best approximates the relationship between the variables.

Use the Correlation and Regression applet for Exercises 91–93.

Question 4.91

91. Create a set of $n = 10$ points such that the correlation coefficient $r$ takes approximately the following values.

Note that you can drag points up or down to adjust your value of $r$ .

$r = 0.90$
$r = - 0.90$
$r = 0.00$

4.1.91

(a)–(c) Answers will vary.

Question 4.92

92. Describe the relationship between the variables for each of the sets of points in the previous exercise.

Question 4.93

93. Select “Show mean $X$ and mean $Y$ lines.” Create a set of $n = 4$ points such that the correlation coefficient $r$ takes approximately the following values. Note that you can drag points up or down to adjust your value of $r$ .

$r = 0.70$
$r = - 0.70$
$r = 0.00$

4.1.93

(a)–(c) Answers will vary.

WORKING WITH LARGE DATA SETS

Chapter 4 Case Study: Measuring the Human Body. Open the data sets body_females body_males. We shall explore the relationships between height and weight for the women and men in these data sets using the tools and techniques we have learned in this section. Use technology to do the following:

Question 4.94

body_females

body_males

94. Construct a scatterplot of weight versus height for the men.

Question 4.95

body_females

body_males

95. Characterize the relationship between male height and weight.

Question 4.96

body_females

body_males

96. Find the correlation coefficient between height and weight for the males.

Question 4.97

body_females

body_males

97. Interpret the correlation coefficient for men's height and weight.

Question 4.98

body_females

body_males

98. Discuss similarities and differences among your results for the females (from the Your Turn exercises in this section) and the males, as follows:

The scatterplots
The relationships between height and weight
The correlation coefficients