5.4 Counting Methods

OBJECTIVES By the end of this section, I will be able to …

  1. Apply the Multiplication Rule for Counting to solve certain counting problems.
  2. Use permutations and combinations to solve certain counting problems.
  3. Compute probabilities using combinations.

Counting methods allow us to solve a range of problems, including how to compute certain probabilities.

1 Multiplication rule for counting

Let us begin with an example illustrating a general rule of counting.

292

EXAMPLE 33 Design your own T-shirt

image

A store at the local mall allows customers to design their own T-shirts. The store offers the following options to its customers:

  • Sleeve type: Long-sleeve or short-sleeve
  • Color: White, black, or red
  • Image: Stock picture or uploaded photo

List the possible T-shirt options.

Solution

Figure 18 is a tree diagram that shows all the different T-shirts that can be designed. Two choices are available for the type of sleeve. For each sleeve type, there are three choices for color. For each color, there are two choices of image: stock picture or uploaded photo. Altogether, customers have a choice from among

different T-shirt options.

NOW YOU CAN DO

Exercises 7–10.

image
Figure 5.20: FIGURE 18 Tree diagram for the different T-shirt options.

293

We can generalize the result from Example 33 as the Multiplication rule for Counting.

Multiplication rule for counting

Suppose an activity consists of a series of events in which there are possible outcomes for the first event, possible outcomes for the second event, possible outcomes for the third event, and so on. Then the total number of different possible outcomes for the series of events is

EXAMPLE 34 Counting with repetition: Famous initials

Some Americans in history are uniquely identified by their initials. For example, “JFK” stands for John Fitzgerald Kennedy, and “FDR” stands for Franklin Delano Roosevelt. How many different possible sets of initials are there for people with a first, middle, and last name?

Solution

Let us consider the three initials as an activity consisting of three events. Note that a particular letter may be repeated, as in “AAM” for A. A. Milne, author of Winnie the Pooh. Then there are ways to choose the first initial, ways to choose the second initial, and ways to choose the third initial. Thus, by the Multiplication Rule for Counting, the total number of different sets of initials is

NOW YOU CAN DO

Exercises 11 and 12.

EXAMPLE 35 Counting without repetition: Intramural singles tennis

Note: To summarize the key difference between Examples 34 and 35: If repetitions are allowed, then . If repetitions are not allowed, then the numbers being multiplied decrease by one from left to right.

A local college has an intramural singles tennis league with five players: Ryan, Megan, Nicole, Justin, and Kyle. The college presents a trophy to the top three players in the league. How many different possible sets of three trophy winners are there?

Solution

The major difference between Example 34 and this example is that, in this example there can be no repetition. Ryan cannot finish in first place and second place. So we proceed as follows: Five possible players could finish in first place, so . Now there are only four players left, one of whom will finish in second place, so . That leaves only three players, one of whom will finish in third place, giving . Thus, by the Multiplication Rule for Counting, the number of different possible sets of trophy winners is

NOW YOU CAN DO

Exercises 13 and 14.

YOUR TURN #21

For the situation in Example 35, suppose there are six players, and the college presents a trophy to the top four players in the league. How many different possible sets of four trophy winners are there?

(The solution is shown in Appendix A.)

294

EXAMPLE 36 Traveling salesman problem

A Southeast regional salesman has eight destinations that he must travel to this month: Atlanta, Raleigh, Charleston, Nashville, Jacksonville, Richmond, Mobile, and Jackson. How many different possible routes could he take?

Solution

The salesman has different choices for where to go first. Once the first destina-tion has been chosen, there are only choices for where to go second. And once the first two destinations have been chosen, there are only choices for where to go third, and so on. Thus, by the Multiplication Law for Counting, the number of dif-ferent possible routes for the salesman is

NOW YOU CAN DO

Exercises 15 and 16.

YOUR TURN #22

For the traveling salesman in Example 36, suppose there are ten destinations he must travel to. How many different possible routes could he take?

(The solution is shown in Appendix A.)

The calculation in Example 36 leads us to introduce the factorial symbol, which is used for the counting rules we will learn in the remainder of this section.

For any integer , the factorial symbol ! is defined as follows:

EXAMPLE 37 Factorials

Calculate the following factorials:

Solution

NOW YOU CAN DO

Exercises 17–22.

YOUR TURN #23

Find the following factorials:

(The solutions are shown in Appendix A.)

295

2 Permutations and combinations

EXAMPLE 38 Traveling to some but not all of the cities

Example 37 calculated the number of possible routes for traveling to cities. However, suppose we are interested in traveling to some but not all of the cities? For example, suppose that the salesman is traveling to three of the eight cities. Find the number of possible routes.

Solution

Eight choices are available for the first city, seven choices for the second city, and six choices for the third city. The salesman is traveling to three cities only, so the number of possible routes is thus

This result may be rewritten using factorial notation, as follows:

NOW YOU CAN DO

Exercises 23 and 24.

YOUR TURN #24

For the traveling salesman in Example 38, suppose there are 10 destinations, but he is traveling only to 5 of the 10 destinations. Find the number of possible routes.

(The solution is shown in Appendix A.)

Example 38 leads us to the following definition.

Permutations

A permutation is an arrangement of items, such that

  • items are chosen at a time from distinct items.
  • repetition of items is not allowed.
  • the order of the items is important.

The number of permutations of items chosen at a time is denoted as and given by the formula

In Example 38, we are looking for the number of permutations of 8 cities taken 3 at a time. We have

EXAMPLE 39 Calculating numbers of permutations

Find the following numbers of permutations:

Solution

  1. 296

NOW YOU CAN DO

Exercises 25–32.

YOUR TURN #25

Find the following numbers of permutations:

(The solution is shown in Appendix A.)

EXAMPLE 40 Counting permutations: Secret Santas

“Secret Santa” refers to a method whereby each member of a group anonymously buys a holiday gift for another member of the group. Each person is secretly assigned to buy a gift for another randomly chosen person in the group. Suppose Jessica, Laverne, Samantha, and Luisa share a dorm suite and want to do Secret Santa this holiday season.

  1. Verify that in this instance one woman purchasing a gift for another woman represents a permutation.
  2. Calculate how many possible different permutations of gift buying there are for the four women.

Solution

    • There are women, and people are associated with each gift (the giver and the receiver).
    • Each person can buy only one gift, so repetition is not allowed.
    • Finally, there is a difference between Jessica buying for Laverne and Laverne buying for Jessica. Thus, order is important, and thus, buying a gift represents a permutation.

  2. The number of permutations is calculated as follows:

In a permutation, order is important. For example, in Example 40, there was a dif-ference between Jessica buying a gift for Laverne and Laverne buying one for Jessica. However, what if we consider shaking hands instead? Then Jessica shaking hands with Laverne is considered the same as Laverne shaking hands with Jessica. Thus, some-times order is not important. What is important here is the combination of Jessica and Laverne.

combinations

A combination is an arrangement of items in which

  • items are chosen from distinct items.
  • repetition of items is not allowed.
  • the order of the items is not important.

The number of combinations of items chosen from different items is denoted as

297

EXAMPLE 41 How many combinations in the intramural tennis league?

We return to the intramural singles tennis league at the local college. There are five players: Ryan, Megan, Nicole, Justin, and Kyle. Each player must play each other once.

  1. Confirm that a match between two players represents a combination.
  2. How many matches will be held?

Solution

  1. Let {Ryan, Megan} denote a tennis match between Ryan and Megan. Note:

    • There are players chosen from players.
    • Each player plays each other player once, so repetition is not allowed.
    • There is no difference between {Ryan, Megan} and {Megan, Ryan}, so order is not important.

    Thus, a tennis match between two players represents a combination.

  2. The list of all matches is as follows.
{Ryan, Megan} {Megan, Nicole} {Nicole, Justin}
{Ryan, Nicole} {Megan, Justin} {Nicole, Kyle}
{Ryan, Justin} {Megan, Kyle} {Justin, Kyle}
{Ryan, Kyle}

Thus, there are possible matches of players chosen from players.

YOUR TURN #26

For the intramural league in Example 41, suppose there are 10 players. How many matches will be held?

(The solution is shown in Appendix A.)

We saw in Example 39 that and in Example 41 that . Permuta-tions and combinations differ only in that ordering is ignored for combinations. To calculate the number of combinations , we have to take into consideration how many different rearrangements there are of the same items. For example, in Example 41, there are rearrangements of the same players, such as {Ryan, Megan} and {Megan, Ryan}. Thus,

In general, the number of combinations can be computed as the number of permu-tations divided by the factorial of the number of items chosen.

Note: Following are some special combinations you may find useful. For any integer :

Formula for the Number of combinations

The number of combinations of items chosen from different items is given by

For instance, in Example 41, the formula for the number of combinations is

Thus, the relation: is verified.

298

EXAMPLE 42 Calculating numbers of combinations

Find the following numbers of combinations:

Solution

NOW YOU CAN DO

Exercises 33–40.

YOUR TURN #27

Find the following numbers of combinations:

(The solutions are shown in Appendix A.)

Note that in (c), we used the commutative property of multiplication and found that . In general, for this reason.

EXAMPLE 43 Calculating the number of permutations and combinations using technology

Use the TI-83/84 and Excel to calculate the following:

Solution

We use the instructions provided in the Step-by-Step Technology Guide at the end of this section (page 302).

  1. From Figures 19a and 19b, we find that

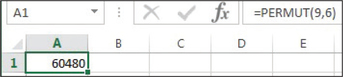    image
    Figure 5.21: FIGURE 19a TI-83/84 permutation results.
    image
    Figure 5.22: FIGURE 19b Excel permutation results.
  2. From Figures 19c and 19d, we find that .
    image
    Figure 5.23: FIGURE 19c TI-83/84 combination results.
    image
    Figure 5.24: FIGURE 19d Excel combination results.

299

Sometimes we wish to find the number of permutations of items where some of the items are not distinct.

EXAMPLE 44 Permutations with nondistinct items

How many distinct strings of letters can we make by using all the letters in the word STATISTICS?

Solution

Each string will be 10 letters long and include 3 S's, 3 T's, 2 I's, 1 A, and 1 C. The 10 positions shown here need to be filled.

The string-forming process is as follows:

  • Step 1 Choose the positions for the three S's.
  • Step 2 Choose the positions for the three T's.
  • Step 3 Choose the positions for the two I's.
  • Step 4 Choose the position for the one A.
  • Step 5 Choose the position for the one C.

There are ways to place the three S's in Step 1. Once Step 1 is done, seven slots are left, leaving positions for the three T's. Once Step 2 is done, four slots are left, so there are ways to place the two I's. Once Step 3 is done, only two slots are left, so there are only ways to position the A. Finally, there is only way to place the C.

Putting Steps 1–5 together, we calculate the number of distinct letter strings as

There are 50,400 distinct strings of letters that can be made using the letters in the word STATISTICS.

This example can be generalized in the following result.

Permutations of Nondistinct Items

The number of permutations of items of which are of the first kind, are of the second kind, …, and are of the kind is calculated as

where

300

EXAMPLE 45 Number of permutations of nondistinct items

Brandon brings a healthy snack to school each day, consisting of 5 carrot sticks, 4 celery sticks, and 2 cherry tomatoes. If Brandon eats one item at a time, in how many different ways can he eat his snack?

Solution

We are seeking the number of permutations of items, of which are carrot sticks, are celery sticks, and are cherry tomatoes. Using the formula for the number of permutations of nondistinct items,

There are 6930 distinct ways in which Brandon can eat his snack.

NOW YOU CAN DO

Exercises 41 and 42.

Acceptance sampling refers to the process of (1) selecting a random sample from a batch of items, (2) evaluating the sample for defectives, and (3) either accepting or rejecting the entire batch based on the evaluation of the sample.

EXAMPLE 46 Acceptance sampling uses combinations

Suppose we have a batch of 20 cell phones, of which, unknown to us, 3 are defective and 17 are nondefective; we will take a random sample of size 2 and evaluate both items once.

  1. Are the arrangements in acceptance sampling permutations or combinations?
  2. Find the number of ways that both sampled cell phones are defective.

Solution

  1. Both permutations and combinations require the following:
    • items are chosen from distinct items. Here, we are selecting phones from a batch of .
    • Repetition of the items is not allowed. Each item is evaluated only once. The difference between permutations and combinations is that, for permutations, order is important, whereas for combinations, order is not important. In acceptance sampling, the order of the items is not important. Thus, acceptance sampling uses combinations.

  2. The number of ways of choosing two of the three defectives is

Selecting 2 defectives means that we are choosing 0 of the 17 nondefectives. The number of ways this can happen is

By the Multiplication Rule for Counting, the number of ways that both sampled cell phones are defective is

301

3 Computing Probabilities Using Combinations

The counting methods we have learned in this section may be used to compute probabilities. We assume that each possible outcome in a random sample is equally likely, and thus we use the classical method for assigning the probability of an event :

EXAMPLE 47 probability using combinations: Acceptance sampling

Continuing with Example 46, if both cell phones in the sample of size 2 are defective,we will reject the batch and cancel our contract with the supplier.

  1. What is the number of ways that both cell phones will be defective?
  2. What is the number of outcomes in this sample space?
  3. What is the probability that both cell phones will be defective?

Solution

  1. From Example 46, the number of ways that both cell phones will be defective is

  2. The number of outcomes in the sample space is given by the number of ways of selecting 2 cell phones out of a batch of 20; that is,

  3. Therefore, the probability that both cell phones will be defective is given by

EXAMPLE 48 Florida Lotto

You can win the jackpot in the Florida Lotto by correctly choosing all 6 winning numbers out of the numbers 1–53.

  1. What is the number of ways of winning the jackpot by choosing all 6 winning numbers?
  2. What is the number of outcomes in this sample space?
  3. If you buy a single ticket for $1, what is your probability of winning the jackpot?
  4. If you mortgage your house and buy 500,000 tickets, what is your probability of winning the jackpot (assuming that all the tickets are different)?

Solution

  1. The number of ways of winning the jackpot by correctly choosing all 6 of the winning numbers and none of the losing numbers is

    302

  2. The size of the sample space is

  3. Therefore, if you buy a single ticket for $1, your probability of winning the jackpot is given by

  4. If you buy 500,000 tickets and they are all unique, then your probability of winning becomes

This is because the unique tickets are mutually exclusive, and the Addition Rule for Mutually Exclusive Events allows us to add the probabilities of the 500,000 tickets.After mortgaging your $500,000 house and buying lottery tickets with the proceeds, there is a better than 97% probability that you will not win the lottery.