5.2 Combining Events
 This page includes Statistical Videos
This page includes Statistical VideosOBJECTIVES By the end of this section, I will be able to …
- Combine events using complement, union, and intersection.
- Apply the Addition Rule to events in general and to mutually exclusive events in particular.
1 Complement, Union, and Intersection
In Example 7, if your roommate rolled a 4, then your roommate was to do your laundry for the rest of the semester. Your roommate is keenly interested in not rolling a 4. If A is an event, then the collection of outcomes not in event A is called the complement of A, denoted Ac. The term complement comes from the word “to complete,” meaning that any event and its complement together make up the complete sample space.
EXAMPLE 14 Finding the probability of the complement of an event
If A is the event “observing a sum of 4 when the two fair dice are rolled,” then your roommate is interested in the probability of Ac, the event that a sum of 4 is not rolled. Find the probability that your roommate does not roll a sum of 4.
Solution
Which outcomes belong to Ac? By the definition, Ac is all the outcomes in the sample space that do not belong in A. The following outcomes are included in A:{(3,1),(2,2)(1,3)}.
Figure 12 shows all the outcomes, except the outcomes from A in the two-dice sample space. There are 33 outcomes in Ac and 36 outcomes in the sample space. The classical probability method then gives the probability of not rolling a sum of 4 to be
P(AC)=N(AC)N(S)=3336=1112

NOW YOU CAN DO
Exercises 7–12.
YOUR TURN#8
Refer to the two-dice sample space on page 247. Define event B as rolling a sum of 8.
- Find P(B).
- Calculate P(Bc).
(The solutions are shown in Appendix A.)
The probability is high that, on this roll at least, your roommate will not land on Boardwalk.
For event A in Example 14, note that
P(A)+P(AC)=112+1112=1
Is this a coincidence, or does the sum of the probabilities of an event and its complement always add to 1? Recall the Law of Total Probability (Section 5.1), which states that the sum of all the outcome probabilities in the sample space must be equal to 1. Because any event A and its complement Ac together make up the entire sample space, then it always happens that P(A)+P(Ac)=1.
Probabilities for complements
For any event A and its complement AC,P(A)+P(AC)=1. Applying a touch of algebra gives the following:
- P(A)=1-P(AC)
- P(AC)=1-P(A)
Sometimes we need to find the probability of a combination of events. For example, consider the casino game of craps in which you roll two dice. One way of winning is by rolling the sum 7 or 11. We can find the probability of the following two events: the sum is 7 or the sum is 11. First, we need some tools for finding the probability of a combination of events.
Union and Intersection of Events
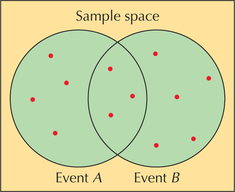
The union of two events A and B is the event representing all the outcomes that belong to A or B or both. The union of A and B is denoted as A∪B and is associated with “or.” In other words, (A∪B)=(A or B).
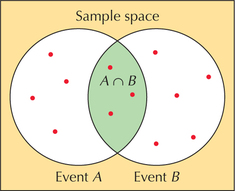
The intersection of two events A and B is the event representing all the outcomes that belong to both A and B. The intersection of A and B is denoted as A∩B and is associated with “and.” In other words, (A∩B)=(A and B).
If you are asked to find the probability of “A or B,” you should find the probability of A ∪ B. Figure 13 shows the union of two events, with the red dots indicating the outcomes. Note from Figure 13 that the union of the events A and B refers to all outcomes in A or B or both. Figure 14 shows that the intersection of the two events is the part where A and B overlap. Both union and intersection are commutative. That is, (A ∪ B)=(B ∪ A)and(A∩B)=(B∩A). In other words, (A or B)=(B or A)and(A and B)=(B and A).
EXAMPLE 15 Union and intersection
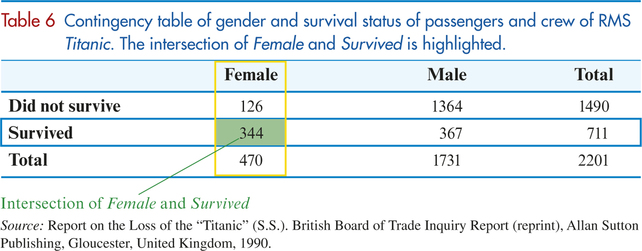
Recall from Section 2.1 that a contingency table (also known as a crosstabulation) is a tabular summary of the relationship between two categorical variables. Table 6 contains a contingency table summarizing the gender and survival status of the passengers and crew of RMS Titanic.
Suppose our experiment is to select one person at random from the passengers and crew. Define the following events:
- F:Person is a female
- S:Person survived
- Find the intersection of these events, (F and S).
- Find the union of these events, (F or F).
Solution
- The intersection of F and S is the event containing the outcomes that are common to both F and S. Note in Table 6 that the female outcomes form a column and the survived outcomes form a row. The intersection of F and S lies at the “intersection” of this column and this row, as illustrated in Table 6. The green cell belongs both to the Female column and the Survived row, and thus belongs to both events. The green cell therefore represents the intersection, (F and S), which includes the 344 passengers and crew who were both female and survived.
- The union of F and S is the event containing all the people who were either female or who survived, or both. That is, the union (F or S) contains the following groups:
- F:Those who were female (126 who did not survive and 344 who did survive)
- S:Those who survived (344 females and 367 males).
Thus, in Table 6, the union (F or S) is represented by the cells containing 126, 344, and 367.
NOW YOU CAN DO
Exercises 13–18.
YOUR TURN#9
Refer to the experiment in Example 15. Define the following events:
- M:Person is a male
- N:Person did not survive
- Find (M and N).
- Find (M or N).
(The solutions are shown in Appendix A.)
2 Addition rule
We are often interested in finding the probability that either one event or another event may occur. The formula for finding these kinds of probabilities is called the Addition Rule.
Addition Rule
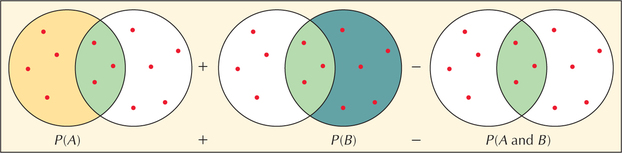
P(A∪B)=P(A)+P(B)-P(A∩B)
In other words,
P(A or B)=P(A)+P(B)-P(A and B)
What Does the Addition Rule Mean?
We can use Figure 15 to understand the Addition Rule. We are trying to find P(A or B), the probability of all the outcomes in A or B or both. The first part of the formula says to add the probabilities of the outcomes in A to those of the outcomes in B. But what about the overlap between A and B, which includes outcomes that belong to both events? To avoid counting the outcomes in the overlap (intersection) twice, we have to subtract the probability of the intersection, P(A and B).
EXAMPLE 16 Addition Rule
Continuing with the RMS Titanic data from Example 15, Table 6 is reproduced here. Find the probability that a randomly chosen passenger or crew member had the following characteristics:
- Was female
- Survived
- Was female and survived
- Was female or survived

Solution
- Here, we seek P(F). There were 470 female passengers and crew among the 2201 people on board the Titanic. Therefore, P(F)=470/2201=0.2135.
- We are looking for P(S). Of the 2201 people on board the Titanic, 711 survived. Thus, P(S)=711/2201=0.3230.
- Those who were female and survived represent the intersection (F and S). In Example 15, we found that these were represented by the green cell with 344 people in it, lying in the intersection of the Female column and the Survived row. Therefore, P(FandS)=344/2201=0.1563.
- Here, we seek P(F or S). By the Addition Rule,
P(ForS)=P(F)+P(S)-P(FandS)=0.2135+0.3230-0.1563=0.3802
NOW YOU CAN DO
Exercises 19–44.
YOUR TURN#10
Refer to the experiment in Example 15. Define the following events:
- M:Person was a male
- N:Person did not survive
Find the probability that a randomly chosen passenger or crew member has the following characteristics:
- Was male
- Did not survive
- Was a male who did not survive
- Was a male or did not survive
(The solutions are shown in Appendix A.)
Mutually Exclusive Events
When drawing a card at random from a deck of 52 cards, the events “a heart is drawn” and “a diamond is drawn” have no outcomes in common. That is, no card is both a heart and a diamond. We say that these two events are mutually exclusive.
Two events are said to be mutually exclusive, or disjoint, if they have no outcomes in common.
Note that any event and its complement are always mutually exclusive. Other examples of mutually exclusive events are given in Table 7.
| Experiment | Mutually exclusive events |
|---|---|
| Draw a single card from a deck of 52 cards | Card is red; card is a spade. |
| Buy a stock | Stock will increase in value; stock will not change in value. |
| Select a student at random | Student is 30 years old or older; student is under 18 years old. |
| Select a college course at random | Course has 3 credits; course has 4 credits. |
Figure 16 shows how mutually exclusive events are represented graphically. It shows the events
A={1,3,5,7,9} and B={0,2,4,6,8}
with sample space S={0,1,2,3,4,5,6,7,8,9}.
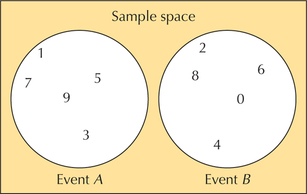
Note that no overlap exists between the two events. When two events are mutually exclusive, they share no outcomes, and therefore the intersection of mutually exclusive events is empty. Because the intersection (A and B) is empty, then for mutually exclusive events, P(A and B)=0. Therefore, we can formulate a special case of the Addition Rule for Mutually Exclusive Events A and B:
P(A or B)=P(A)+P(B)-P(A and B)=P(A)+P(B)-0=P(A)+P(B)
Addition Rule for Mutually Exclusive Events
If A and B are mutually exclusive events, P(AorB)=P(A)+P(B).
EXAMPLE 17 Addition Rule for mutually exclusive events
The National Center for Education Statistics conducted a survey regarding the living arrangements of 19,735 college students. The results are shown in Table 8.
| On campus | Off campus | With parents | Total | |
|---|---|---|---|---|
| Females | 1,368 | 5,741 | 4,103 | 11,212 |
| Males | 1,240 | 4,170 | 3,113 | 8,523 |
| Total | 2,608 | 9,911 | 7,216 | 19,735 |
Calculate the following probabilities for a randomly chosen college student:
- Lives on campus, P(C).
- Lives with parents, P(W).
- Lives on campus or with parents, P(C or W).
Solution
- A total of 2,608 of the 19,735 students live on campus, so P(C)=2,608/19,735=0.1322.
- Of the 19,735 students, 7,216 live with parents, so P(W)=7,216/19,735=0.3656.
- Living on campus and living with parents are mutually exclusive. So, by the Addition Rule for Mutually Exclusive Events, P(CorW)=P(C)+P(W)=0.1322+0.3656=0.4978.
NOW YOU CAN DO
Exercises 45–48.
YOUR TURN#11
Refer to Example 17. Find the probability that a randomly chosen student lives on campus or lives off campus.
(The solution is shown in Appendix A.)