8 Confidence Intervals

8.4 Confidence Intervals for the Population Variance and Standard Deviation

OBJECTIVES By the end of this section, I will be able to …

Describe the properties of the $χ^{2}$ (chi-square) distribution, and find critical values for the $χ^{2}$ distribution.
Construct and interpret confidence intervals for the population variance and standard deviation.

We have seen how confidence intervals can be used to estimate the unknown value of a population mean or a population proportion. However, the variability of a population is also important. As we have learned, less variability is usually better. For example, a tool manufacturer relies on a quality control technician (who has a strong background in statistics) to make sure that the tools the company is making do not vary appreciably from the required specifications. Otherwise, the tools may be too large or too small. Data analysts therefore construct confidence intervals to estimate the unknown value of the population parameters that measure variability: the population variance $σ^{2}$ and the population standard deviation $σ$ .

Page 474

We first need to become acquainted with the $χ^{2}$ (chi-square) distribution, which is used to construct these confidence intervals.

1 Properties of the $χ^{2}$ (chi-Square) Distribution

The $χ^{2}$ (pronounced ky-square, to rhyme with “my square”) distribution was discovered in 1875 by the German physicist Friedrich Helmert and further developed in 1900 by the English statistician Karl Pearson. It is a continuous distribution, so the $χ^{2}$ random variable is continuous.

Just as we did with the normal and $t$ distributions, we can find probabilities associated with values of $χ^{2}$ , and vice versa. Similar to any continuous distribution, probability is represented by area below the curve above an interval. We examine the properties of the $χ^{2}$ distribution and then learn how to use the $χ^{2}$ table to find the critical values of the $χ^{2}$ distribution.

Properties of the $χ^{2}$ Distribution

Just as for any continuous random variable, the total area under the $χ^{2}$ curve equals 1.
The value of the $χ^{2}$ random variable is never negative, so the $χ^{2}$ curve starts at 0. However, it extends indefinitely to the right, with no upper bound.
Because of the characteristics just described, the $χ^{2}$ curve is right-skewed.
There is a different curve for every different degrees of freedom, $n - 1$ . As the number of degrees of freedom increases, the $χ^{2}$ curve begins to look more symmetric (Figure 34).

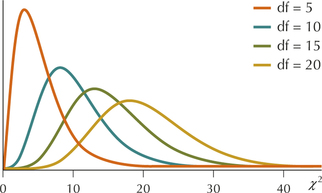FIGURE 34 Shape of the $χ^{2}$ distribution for different degrees of freedom.

To construct the confidence intervals in this section, we will need to find the critical values of a $χ^{2}$ distribution for the given confidence level $100 (1 - α) %$ , using either the $χ^{2}$ table (Table E in the Appendix) or technology. The $χ^{2}$ table is somewhat similar to the $t$ table (Table D in the Appendix); both tables show the degrees of freedom in the left column. The area to the right of the $χ^{2}$ critical value is given across the top of the table.

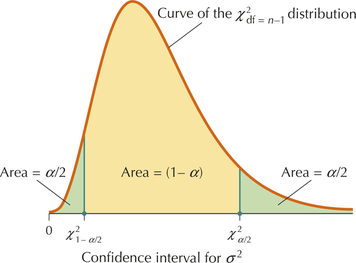
The $χ^{2}$ distribution is not symmetric, so we cannot construct the confidence interval for $σ^{2}$ using the “point estimate ± margin of error” method. Instead, the lower bound and upper bound for the confidence interval are determined using two $χ^{2}$ critical values:

$X_{1 - α / 2}^{2}$ = the value of the $χ^{2}$ distribution with area $1 - α / 2$ to its right (Figure 35)

$X_{α / 2}^{2}$ = the value of the $χ^{2}$ distribution with area $1 - α /2$ to its right (Figure 35)

Page 475

For instance, for a 95% confidence interval $(1 - α) = 0.95$ , $α / 2 = 0.025$ and $1 - α / 2 = 0.975$ . Thus, $χ_{0.975}^{2}$ represents the value of the $χ^{2}$ distribution with area $1 - α / 2 = 0.975$ to the right of the $χ^{2}$ critical value. The second critical value $X_{0.025}^{2}$ represents the value of the $χ^{2}$ distribution with area $α / 2 = 0.025$ to the right of the $χ^{2}$ critical value.

FIGURE 35

$χ^{2}$ critical values.

EXAMPLE 23 Finding the $χ^{2}$ critical values

Note: If the appropriate degrees of freedom are not given in the $χ^{2}$ table, the conservative solution is to take the next row with the smaller df.

Find $χ^{2}$ critical values for a 90% confidence interval, where we have a sample size of size $n = 10$ .

Solution

For a 90% confidence interval,

$\begin{matrix} (1 - α) = 0.90 & \frac{α}{2} = \frac{0.10}{2} = 0.05 & 1 - \frac{α}{2} = 1 - 0.05 = 0.95 \end{matrix}$

So we are seeking (1) $χ_{0.95}^{2}$ , the critical value with area $1 - α / 2 = 0.95$ to the right of it, and (2) $χ_{0.05}^{2}$ , the critical value with area $α / 2 = 0.05$ to the right of it.

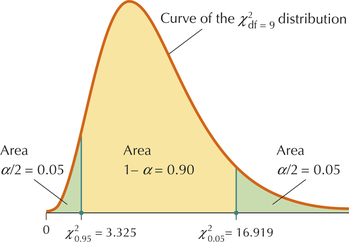
Because $n = 10$ , the degrees of freedom is $df = n - 1 = 10 - 1 = 9$ . To find $χ_{0.95}^{2}$ for df = 9, go across the top of the $χ^{2}$ table (Table E in the Appendix) until you see 0.95 (Figure 36). $χ_{0.95}^{2}$ is somewhere in that column. Now go down that column until you see your number of degrees of freedom df = 9. Thus, for df = 9, $χ_{0.95}^{2} = 3.325$ . For a $χ^{2}$ distribution with 9 degrees of freedom, there is area = 0.95 to the right of 3.325.

FIGURE 36 Finding

$χ_{0.95}^{2}$ and

$χ_{0.05}^{2}$ using the

$χ^{2}$ table.

Page 476

Similarly, $χ_{0.05}^{2}$ is found in the column labeled “0.05” and the row corresponding to $df = 9$ . We find that $χ_{0.05}^{2} = 16.919$ , as shown in Figure 37.

FIGURE 37

$χ^{2}$ critical values for the

$χ^{2}$ distribution with df = 9.

NOW YOU CAN DO

Exercises 9–16.

YOUR TURN#16

Find $χ^{2}$ critical values for a 95% confidence interval, where we have a sample size of size $n = 20$ .

(The solutions are shown in Appendix A.)

2 Constructing Confidence Intervals for the Population Variance and Standard Deviation

We derive the formula for a $100 (1 - α) %$ confidence interval for the population variance $σ^{2}$ . Suppose we take a random sample of size $n$ from a normal population with mean $μ$ and standard deviation $σ$ . Then the statistic

$χ^{2} = \frac{(n - 1) s^{2}}{σ^{2}}$

follows a $χ^{2}$ distribution with $n - 1$ degrees of freedom, where $s^{2}$ represents the sample variance. From Figure 35, we see that $100 (1 - α) %$ of the values of $χ^{2}$ lie between $χ_{1 - α / 2}^{2}$ and $χ_{α / 2}^{2}$ . These values are described as

$χ_{1 - α / 2}^{2} < \frac{(n - 1) s^{2}}{σ^{2}} < χ_{α / 2}^{2}$

Rearranging this inequality so that $σ^{2}$ is in the numerator gives us the formula for the $100 (1 - α) %$ confidence interval for $σ^{2}$ :

$\frac{(n - 1) s^{2}}{χ_{α / 2}^{2}} < σ^{2} < \frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2}}$

Thus, the lower bound of the confidence interval for $σ^{2}$ is $\frac{(n - 1) s^{2}}{χ_{α / 2}^{2}}$ , and the upper bound is $\frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2}}$ . Taking the square root of each gives us the lower and upper bounds or the confidence interval for $σ$ .

Confidence Interval for the Population Variance $σ^{2}$

Suppose we take a sample of size $n$ from a normal population with mean $μ$ and standard deviation $σ$ . Then a $100 (1 - α) %$ confidence interval for the population variance $σ^{2}$ is given by

$lower bound = \frac{(n - 1) s^{2}}{χ_{α / 2}^{2}}, upper bound = \frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2}}$

where $s^{2}$ represents the sample variance and $χ_{1 - α / 2}^{2}$ and $χ_{α / 2}^{2}$ are the critical values for a $χ^{2}$ distribution with $n − 1$ degrees of freedom.

Page 477

Confidence Interval for the Population Standard Deviation $σ$

A $100 (1 - α) %$ confidence interval for the population standard deviation $σ$ is then given by

$lower bound = \sqrt{\frac{(n - 1) s^{2}}{χ_{α / 2}^{2}}}, upper bound = \sqrt{\frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2}}}$

EXAMPLE 24 Constructing confidence intervals for the population variance $σ^{2}$ and population standard deviation $σ$

electricmiles

The accompanying table shows the miles-per-gallon equivalent (MPGe) for fve electric cars, as reported by www.hybridcars.com in 2014. The normal probability plot in Figure 38 indicates that the data are normally distributed.

FIGURE 38 Normal probability plot of miles-per-gallon equivalent for fve electric cars.

Electric Vehicle	Mileage (MPGe)
Tesla Model S	89
Nissan Leaf	99
Ford Focus	105
Mitsubishi i-MiEV	112
Chevrolet Spark	119

Find the critical values $χ_{1 - α / 2}^{2}$ and $χ_{α / 2}^{2}$ for a confidence interval with a 95% confidence level.
Construct and interpret a 95% confidence interval for the population variance of electric car MPG.
Construct and interpret a 95% confidence interval for the population standard deviation of electric car MPG.

electricmiles

Solution

There are $n = 5$ electric cars in our sample, so the degrees of freedom equal $n - 1 = 4$ .

For a 95% confidence interval,

$\begin{matrix} (1 - α) = 0.95 & α / 2 = 0.025 & 1 - α / 2 = 0.975 \end{matrix}$

From the $χ^{2}$ table (Table E in the Appendix), therefore,

$\begin{matrix} χ_{1 - α / 2}^{2} = χ_{0.975}^{2} = 0.484 & χ_{α / 2}^{2} = χ_{0.025}^{2} = 11.143 \end{matrix}$

Figures 39 through 41 show these results using Excel, Minitab, and JMP.
Figure 42 shows the descriptive statistics for MPGe, as obtained by the TI-83/84. The sample standard deviation is $s = 11.58447237$ .

Page 478

FIGURE 39 Excel results.

FIGURE 40 Minitab results.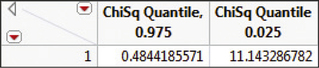

FIGURE 41 JMP results.

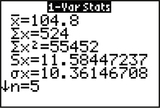FIGURE 42 TI-83/84 results.

Thus, our 95% confidence interval for $σ^{2}$ is given by

$\begin{array}{l} lower bound = \frac{(n - 1) s^{2}}{χ_{α / 2}^{2}} = \frac{(4) {11.58447237}^{2}}{11.143} \approx 48.1737414 \approx 48.17 \\ upper bound = \frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2}} = \frac{(4) {11.58447237}^{2}}{0.484} \approx 1109.09091 \approx 1109.09 \end{array}$

We are 95% confident that the population variance $σ^{2}$ lies between 48.17 and 1109.09 miles per gallon squared, that is, (MPG)². (Recall that the variance is measured in units squared.) It is unclear what miles per gallon squared means, so we prefer to construct a confidence interval for the population standard deviation $σ$ .
Using the results from part (b),
$\begin{array}{l} lower bound = \sqrt{\frac{(n - 1) s^{2}}{χ_{α / 2}^{2}}} = \sqrt{48.1737414} \approx 6.94073061 \approx 6.94 \\ upper bound = \sqrt{\frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2}}} = \sqrt{1109.09091} \approx 33.30301653 \approx 33.3 \end{array}$

We are 95% confident that the population standard deviation $σ$ lies between 6.94 and 33.3 miles per gallon. Figure 43 shows the two confidence intervals obtained using Minitab.

FIGURE 43 Minitab results showing the confidence intervals.

Figure 44 shows the confidence interval for $σ$ obtained using JMP. We are interested in the bottom row, which has the confidence interval for the population standard deviation $σ$ .

FIGURE 44 JMP results showing the confidence interval for

$σ$ .

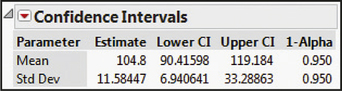
NOW YOU CAN DO

Exercises 17–32.