Section 8.2 Exercises

CLARIFYING THE CONCEPTS

Question 8.98

1. Why do we need the interval? Why can't we always use intervals? (pp. 448–449)

8.2.1

In most real-world problems, the population standard deviation is unknown, so we can't use the interval.

Question 8.99

2. Suppose that is known. Should we still use a interval? (p. 453)

Question 8.100

3. As the sample size gets larger and larger, what happens to the curve? (p. 450)

8.2.3

The curve approaches closer and closer to the curve.

Question 8.101

4. State the formula for the margin of error for the interval. (p. 454)

PRACTICING THE TECHNIQUES

image CHECK IT OUT!

To do Check out Topic
Exercises 5–8 Example 12 Finding
Exercises 9–12 Example 13 Checking whether the
conditions are met for
the interval for
Exercises 13–28 Example 14 Constructing a
confidence interval
for
Exercises 29–40 Example 15 Margin of error

Question 8.102

5. For the following scenarios, we are taking a random sample from a normal population with unknown. Find .

  1. Confidence level 90%, sample size 21
  2. Confidence level 95%, sample size 21
  3. Confidence level 99%, sample size 21

8.2.5

(a) 1.725 (b) 2.086 (c) 2.845

Question 8.103

6. For the following scenarios we are taking a random sample from a normal population with unknown. Find .

  1. Confidence level 95%, sample size 11
  2. Confidence level 95%, sample size 21
  3. Confidence level 95%, sample size 31

Question 8.104

7. Refer to Exercise 5.

  1. Describe what happens to the value of , as the confidence level increases, for a given sample size.
  2. Draw a sketch of the curve for sample size , and explain why the value of changes as it does.

8.2.7

(a) For a given sample size, the value of increases as the confidence level increases. (b) As the value of increases, the confidence interval becomes wider. With a wider confidence interval you can be more confident that your confidence interval contains μ.

image

Question 8.105

8. Refer to Exercise 6.

  1. Describe what happens to the value of , as the sample size increases, for a given confidence level.
  2. Draw a sketch of the curve for a confidence level of 95%, and explain why the value of changes as it does.

For each of Exercises 9–12, we are taking a random sample from a population with unknown. Check whether the conditions are met for constructing the indicated interval for . If not, explain why not.

Question 8.106

9. Confidence level 95%, , ,

8.2.9

The sample size is not large ( is not ) and we are not told that the population is normal. Therefore, the conditions are not met for the interval for μ. It is not okay to construct the interval.

Question 8.107

10. Confidence level 99%, , , , normal population

458

Question 8.108

11. Confidence level 95%, , ,

8.2.11

We are not told that the population is normal. However, the sample size is large ( is ). Therefore, the conditions are met for the interval for μ. It is okay to construct the interval.

Question 8.109

12. Confidence level 90%, , ,

For the data sets shown in Exercises 13–16, assume the populations are normal, and do the following:

  1. Calculate and .
  2. Find .
  3. Construct and interpret a 95% confidence interval for .

Question 8.110

13.

4 5 3 5 3

8.2.13

(a) (b) (c) (2.759, 5.241). We are 95% confident that the population mean lies between 2.759 and 5.241.

Question 8.111

14.

18 14 16 14 18

Question 8.112

15.

10 16 13 16 10

8.2.15

(a) (b) (c) (9.276, 16.724). We are 95% confident that the population mean lies between 9.276 and 16.724.

Question 8.113

16.

100 108 104 100 108

For Exercises 17–22, we are taking a random sample from a normal population with unknown.

  1. Find .
  2. Confirm that the requirements are met for the confidence interval for .
  3. Construct the confidence interval for with the indicated confidence level.
  4. Sketch the confidence interval on a number line.

Question 8.114

17. Confidence level 90%, sample size 16, sample mean 10, sample standard deviation 5

8.2.17

(a) (b) We are told that the population is normal. (c) (7.8, 12.2); We are 90% confident that the population mean lies between 7.8 and 12.2.

(d)

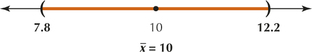
image

Question 8.115

18. Confidence level 95%, sample size 16, sample mean 22, sample standard deviation 3

Question 8.116

19. Confidence level 99%, , ,

8.2.19

(a) (b) We are told that the population is normal. (c) (43.3, 56.7). We are 99% confident that the population mean lies between 43.3 and 56.7.

(d)

image

Question 8.117

20. Confidence level 95%, , ,

Question 8.118

21. Confidence level 95%, , ,

8.2.21

(a) (b) We are told that the population is normal. (c) (−20.6, −19.4). We are 95% confident that the population mean lies between −20.6 and −19.4.

(d)

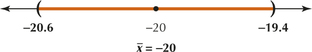
image

Question 8.119

22. Confidence level 90%, , ,

For Exercises 23–28, we are taking a random sample from a population with unknown. However, do not assume that the population is normally distributed.

  1. Find .
  2. Confirm that the requirements are met for the confidence interval for .
  3. Construct the confidence interval for with the indicated confidence level.
  4. Sketch the confidence interval on a number line.

Question 8.120

23. Confidence level 90%, sample size 256, sample mean 100, sample standard deviation 16.

8.2.23

(a) (b) We are not told that the population is normal. However, the sample size is large ( is ). (c) (98.3, 101.7). We are 90% confident that the population mean lies between 98.3 and 101.7.

(d)

image

Question 8.121

24. Confidence level 95%, sample size 100, sample mean 250, sample standard deviation 10.

Question 8.122

25. Confidence level 90%, , ,

8.2.25

(a) (b) We are not told that the population is normal. However, the sample size is large ( is ). (c) (34.4, 35.6). We are 90% confident that the population mean lies between 34.4 and 35.6.

(d)

image

Question 8.123

26. Confidence level 99%, , ,

Question 8.124

27. Confidence level 95%, , ,

8.2.27

(a) (b) We are not told that the population is normal. However, the sample size is large ( is ). (c) (−21, −19). We are 95% confident that the population mean lies between −21 and −19.

(d)

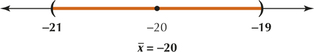
image

Question 8.125

28. Confidence level 95%, , ,

For Exercises 29–40, calculate and interpret the margin of error for the confidence interval from the indicated exercise.

Question 8.126

29. Exercise 17

8.2.29

. We can estimate the population mean to within 2.2 with 90% confidence.

Question 8.127

30. Exercise 18

Question 8.128

31. Exercise 19

8.2.31

. We can estimate the population mean to within 6.7 with 99% confidence.

Question 8.129

32. Exercise 20

Question 8.130

33. Exercise 21

8.2.33

. We can estimate the population mean to within 0.6 with 95% confidence.

Question 8.131

34. Exercise 22

Question 8.132

35. Exercise 23

8.2.35

. We can estimate the population mean to within 1.7 with 90% confidence.

Question 8.133

36. Exercise 24

Question 8.134

37. Exercise 25

8.2.37

. We can estimate the population mean to within 0.6 with 90% confidence.

Question 8.135

38. Exercise 26

Question 8.136

39. Exercise 27

8.2.39

. We can estimate the population mean to within 1 with 95% confidence.

Question 8.137

40. Exercise 28

APPLYING THE CONCEPTS

Question 8.138

41. Hospital Length of Stay. The U.S. Agency for Healthcare Research and Quality reports that the mean length of stay in the hospital for patients suffering from acute myocardial infarction (heart attack) was 4.8 days. Suppose a sample of 31 heart attack patients had a mean length of stay of 4.8 days, with a sample standard deviation of 3 days. Do the following:

  1. State how the conditions for the interval for are met.
  2. Find for a confidence interval with 95% confidence.
  3. Construct and interpret a 95% confidence interval for the population mean length of stay for all heart attack victims.

8.2.41

(a) We are not told that the population is normal. However, the sample size is large ( is ). (b) (c) (3.7, 5.9). We are 95% confident that μ, the population mean length of stay in hospital for all heart attack victims, lies between 3.7 days and 5.9 days.

Question 8.139

42. Student loans. The Pew Research Center (www.pewresearch.org) reports that the mean student loan amount in 2010 was $26,682. Suppose a sample of 41 students had a sample mean loan amount of $26,682 and a sample standard deviation student loan amount of $20,000. Do the following:

  1. State how the conditions for the interval for are met.
  2. Find for a confidence interval with 90% confidence.
  3. Construct and interpret a 90% confidence interval for the population mean student loan amount.

Question 8.140

43. Consumer Sentiment. The University of Michigan Surveys of Consumers found that the mean index of consumer sentiment for December 2013 was 82.5. Suppose this result was based on a sample of size 100, which had a standard deviation of 10.

  1. State how the conditions for the interval for are met.
  2. Find for a confidence interval with 95% confidence.
  3. Construct and interpret a 95% confidence interval for the population mean consumer sentiment.

8.2.43

(a) We are not told that the population is normal. However, the sample size is large ( is ). (b) (c) (80.5, 84.5). We are 95% confident that μ, the population mean consumer sentiment for all consumers, lies between 80.5 and 84.5.

Question 8.141

44. Teachers' Salaries. The Digest of Educational Statistics reported that the mean salary for teachers in 2012 was $56,410. Assume that the sample size was 101 and the sample standard deviation was $15,000.

  1. State how the conditions for the interval for are met.
  2. Find for a confidence interval with 90% confidence.
  3. Construct and interpret a 90% confidence interval for the population mean teacher salary.

459

Question 8.142

45. Hospital Length of Stay. Refer to Exercise 41.

  1. Calculate and interpret the margin of error.
  2. If the sample size is increased to 400, describe what will happen to the margin of error.

8.2.45

(a) days. We can estimate the population mean length of stay in hospital of all heart attack victims to within 1.1 days with 95% confidence. (b) It decreases.

Question 8.143

46. Student Loans. Refer to Exercise 42.

  1. Calculate and interpret the margin of error.
  2. If the sample size is increased to 100, describe what will happen to the margin of error.

Question 8.144

47. Consumer Sentiment. Refer to Exercise 43.

  1. Compute the margin of error and interpret it.
  2. Describe two ways of reducing this margin of error. Which method is more desirable, and why?

8.2.47

(a) . We can estimate the population mean consumer sentiment for all consumers to within 2 with 95% confidence. (b) Decrease the confidence level or increase the sample size; Increase the sample size; The only way to have both high confidence and a tight interval is to boost the sample size.

Question 8.145

48. Teachers' Salaries. Refer to Exercise 44.

  1. Compute the margin of error and interpret it.
  2. Describe two ways of reducing this margin of error. Which method is more desirable, and why?

For Exercises 49–56, software output for confidence intervals for are provided. Assume the conditions are met. For each, examine the indicated software output, and do the following:

  1. Report the confidence interval in the form “(lower bound, upper bound).”
  2. Interpret the confidence interval.
  3. Calculate the margin of error for the confidence interval.
  4. Interpret the margin of error.

Question 8.146

49. Exam Scores. TI-83/84 output, where represents the population mean exam score. Confidence level is 95%.

image

8.2.49

(a) (72.2, 77.8) (b) We are 95% confident that μ, the population mean exam score for all exam takers, lies between 72.2 and 77.8. (c) 2.8 (d) We can estimate the population mean exam score for all exam takers to within 2.8 with 95% confidence.

Question 8.147

50. Clothing Store Sales. Minitab output, where represents the population mean total net sales for a clothing store.

image

Question 8.148

51. Vegetable Farms. SPSS output, where represents the population mean number of vegetable farms per county, nationwide.

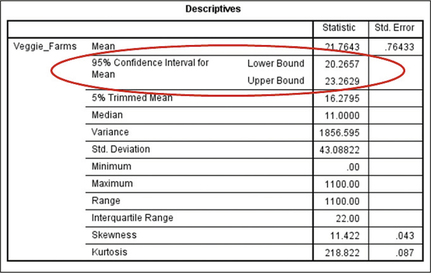
image

8.2.51

(a) (20.3, 23.3) (b) We are 95% confident that μ, the population mean number of vegetable farms per county for all counties nationwide, lies between 20.3 vegetable farms per county and 23.3 vegetable farms per county. (c) 1.5 vegetable farms per county (d) We can estimate the population mean number of vegetable farms per county for all counties nationwide to within 1.5 vegetable farms per county with 95% confidence.

Question 8.149

52. Grocery Stores. JMP output, where represents the population mean number of grocery stores per county, nationwide.

image

Question 8.150

53. Small Businesses. Crunchit! Output, where represents the population mean number of small businesses per city, nationwide. Note: The notation “” means to move the decimal place four places to the right. So, “,” moving the decimal place four places to the right, gives us 22,400.

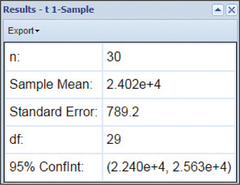
image

8.2.53

(a) (22,400, 25,630) (b) We are 95% confident that μ, the population mean number of small businesses per city for all cities nationwide, lies between 22,400 small businesses per city and 25,630 small businesses per city. (c) 1615 small businesses per city (d) We can estimate the population mean number of small businesses per city for all cities nationwide to within 1615 small businesses per city with 95% confidence.

Question 8.151

54. Protein Content in Breakfast Cereal. For the SPSS output, represents the population mean amount of protein, in grams, for all breakfast cereals.

image

Question 8.152

55. Sugar Content in Breakfast Cereal. For the JMP output, represents the population mean amount of sugars, in grams, for all breakfast cereals.

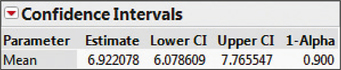
image

8.2.55

(a) (6.08, 7.77) (b) We are 90% confident that μ, the population mean amount of sugar for all breakfast cereals, lies between 6.08 grams and 7.77 grams. (c) 0.84 gram (d) We can estimate the population amount of sugar for all breakfast cereals to within 0.84 gram with 90% confidence.

Question 8.153

56. Fourth-Graders' Feet. For the CrunchIt! Output, represents the population mean length of fourth-graders' feet, in cm.

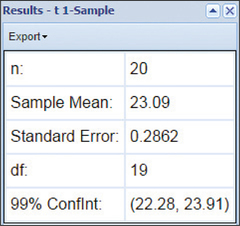
image

460

Question 8.154

carbon

57. Carbon Emissions. The Excel output shows the carbon emissions (in millions of tons) from consumption of fossil fuels for a random sample of five nations.12 The sample mean (using the function “average”) and the sample standard deviation (using the function “stdev”) are also given. The highlighted cell is the margin of error given by the function CONFIDENCE.T, which needs the following values: , , and . Below, the normal probability plot is given.

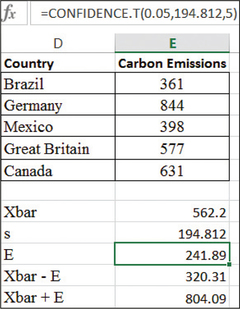
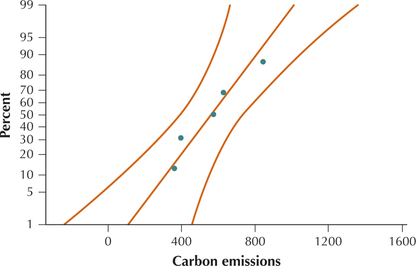
image
image
  1. Check the normality assumption.
  2. Use the Excel output to report and interpret a 95% confidence interval for the population mean carbon emissions.
  3. Use the Excel output to report and interpret the margin of error for the confidence interval in part (b).
  4. Explain two ways we could decrease the margin of error. Which method is preferable, and why?

8.2.57

(a) Acceptable normality (b) (320.31, 804.09). We are 95% confident that μ, the population mean carbon emissions for all nations, lies between 320.31 million tons and 804.09 million tons. (c) million tons; We can estimate the population mean carbon emissions for all nations to within 241.89 million tons with 95% confidence. (d) Decrease the confidence level or increase the sample size. Increase the sample size. The only way to have both high confidence and a tight interval is to boost the sample size.

Question 8.155

deepwaterclean

58. Deepwater Horizon Cleanup Costs. The Excel output shows the amount of money disbursed by BP to a random sample of six Florida counties for cleanup of the Deepwater Horizon oil spill, in millions of dollars.13 The functions used to provide the confidence interval are similar to those in Exercise 57. The normal probability plot is also given.

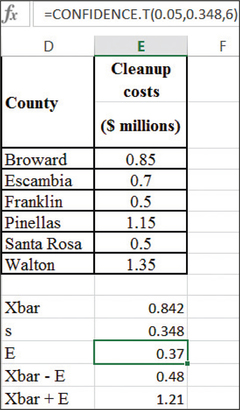
image
image
  1. Check the normality assumption.
  2. Use the Excel output to report and interpret a 95% confidence interval for the population mean cleanup cost.
  3. Use the Excel output to report and interpret the margin of error for the confidence interval in part (b).
  4. Explain two ways we could decrease the margin of error. Which method is preferable, and why?

Question 8.156

wiisales

59. Wii Game Sales. The following table represents the number of units sold (in 1000s) in the United States for the week ending March 26, 2011, for a random sample of 8 Wii games.14 The normal probability plot is given.

Game Units
(1000s)		 Game Units
(1000s)
Wii Sports Resort 65 Zumba Fitness 56
Super Mario All
Stars		 40 Wii Fit Plus 36
Just Dance 2 74 Michael Jackson 42
New Super Mario
Brothers		 16 Lego Star Wars 110
Table 8.20: Source: www.vgchartz.com, April 1, 2011.

461

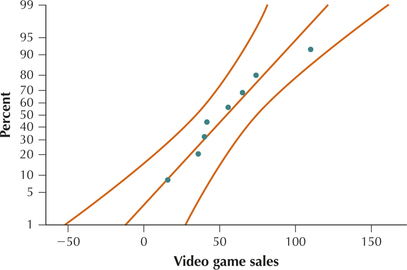
image
  1. Confirm that the normality condition is met.
  2. Construct and interpret a 95% confidence interval for the population mean number of units sold.
  3. Calculate and interpret the margin of error.
  4. How could we decrease the margin of error of our confidence interval without decreasing the confidence level?

8.2.59

(a) Acceptable normality (b) (31, 79). We are 95% confident that μ, the population mean number of Wii game units sold per week for all weeks, lies between 31 thousand units and 79 thousand units. (c) thousand units. We can estimate the population mean number of Wii game units sold per week for all weeks to within 24 thousand units with 95% confidence. (d) Decrease the confidence level or increase the sample size. Increase the sample size. The only way to have both high confidence and a tight interval is to boost the sample size.

Question 8.157

georgiarain

60. A Rainy Month in Georgia? The following table represents the total rainfall (in inches) for the month of February 2011 for a random sample of 10 locations in Georgia.15

Location Rainfall
(inches)		 Location Rainfall
(inches)
Athens 4.72 Atlanta 4.25
Augusta 4.31 Cartersville 3.03
Dekalb 2.96 Fulton 4.36
Gainesville 4.06 Lafayette 3.75
Marietta 3.20 Rome 3.26
Table 8.21: Source: National Weather Service.
  1. Use technology to construct a normal probability plot to confirm that the data exhibit acceptable normality.
  2. Construct and interpret a 90% confidence interval for the population mean rainfall in inches.
  3. Calculate and interpret the margin of error.
  4. How could we decrease the margin of error of our confidence interval without decreasing the confidence level?

Question 8.158

electricmiles

61. Electric Cars. The accompanying table shows the miles-per-gallon equivalent (MPGe) for five electric cars, as reported by www.hybridcars.com in 2014.

Electric Vehicle MPGe
Tesla Model S 89
Nissan Leaf 99
Ford Focus 105
Mitsubishi i-MiEV 112
Chevrolet Spark 119
  1. Use technology to construct a normal probability plot of MPGe. Confirm that the distribution is normal.
  2. Find for a confidence interval with 90% confidence.
  3. Compute and interpret the margin of error for a confidence interval with 90% confidence.
  4. Construct and interpret a 90% confidence interval ( interval) for the population mean mileage.

8.2.61

(a)

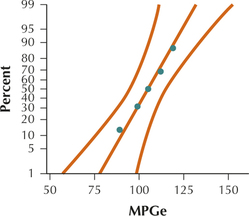
image

Acceptable normality. (b) (c) MPGe. We can estimate the population mean mileage to within 11.0 MPGe with 90% confidence.

(d) (93.8, 115.8). We are 90% confident that μ, the population mean mileage, lies between 93.8 MPGe and 115.8 MPGe.

Question 8.159

cerealcalories

62. Calories in Breakfast Cereals. What is the mean number of calories in a bowl of breakfast cereal? A random sample of six well-known breakfast cereals yielded the following calorie data:

Cereal Calories
Apple Jacks 110
Cocoa Puffs 110
Mueslix 160
Cheerios 110
Corn Flakes 100
Shredded Wheat 80
  1. Use technology to construct a normal probability plot of the number of calories.
  2. Is there evidence that the distribution is not normal?
  3. Can we proceed to construct a interval? Why or why not?

Question 8.160

commutedist

63. Commuting Distances. A university is trying to attract more commuting students from the local community. As part of the research into the modes of transportation students use to commute to the university, a survey was conducted asking how far commuting students commuted from home to school each day. A random sample of 30 students provided the distances (in miles) shown.

14 10 14 12 12 11 5 6 9 14 9 9 4 7 15
9 7 7 12 10 15 10 6 11 9 11 10 11 7 12
  1. Find for a confidence interval with 90% confidence.
  2. Compute and interpret the margin of error for a confidence interval with 90% confidence.
  3. Construct and interpret a 90% confidence interval for the population mean commuting distance.

8.2.63

(a) (b) mile. We can estimate the population mean commuting distance to within 0.9 mile with 90% confidence. (c) (9.0, 10.8). We are 90% confident that μ, the population mean commuting distance, lies between 9.0 miles and 10.8 miles.

Question 8.161

image 64. Refer to the previous exercise. What if we increased the sample size to some unspecified value but everything else stayed the same. Describe what, if anything, would happen to each of the following measures and why:

  2. Margin of error
  3. Width of the confidence interval

462

Cigarette Consumption. Use the following information for Exercises 65–67. Health officials are interested in estimating the population mean number of cigarettes smoked annually per capita in order to evaluate the efficacy of their antismoking campaign. A random sample of eight U.S. counties yielded the following numbers of cigarettes smoked per capita: 2206, 2391, 2540, 2116, 2010, 2791, 2392, 2692.

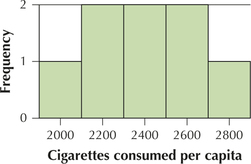
image

Question 8.162

65. Evaluate the normality assumption using the accompanying histogram. Is it appropriate to construct a interval using this data set? Why or why not? What is it about the histogram that tells you one way or the other?

8.2.65

The graph is symmetric about the middle value with the values with the highest frequency in the middle. This indicates that the normality assumption is valid. Since the normality assumption appears to be valid and is unknown, Case 1 applies, so we can use the interval.

Question 8.163

66. Compute and interpret the margin of error for a confidence interval with 90% confidence. What is the meaning of this number?

Question 8.164

67. Construct and interpret a 90% confidence interval for the population mean number of cigarettes smoked per capita.

8.2.67

(2208, 2576). We are 90% confident that μ, the population mean number of cigarettes smoked per capita, lies between 2208 cigarettes and 2576 cigarettes.

Question 8.165

68. Baby Weights. A random sample of 20 babies born in Brisbane (Australia) Hospital had the histogram of the babies' weights shown here. The sample mean is 3227 grams, and the sample standard deviation is 560 grams. Discuss the normality of the data. Do the data appear acceptably normal? Is it appropriate to apply the interval or not? Explain why or why not.

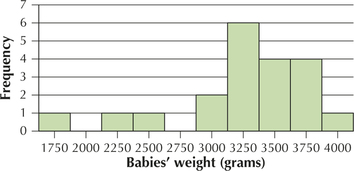
image

BRINGING IT ALL TOGETHER

image Chapter 8 Case Study: Motor Vehicle Fuel Efficiency.

Use the following information for Exercises 69–74. The Environmental Protection Agency calculates the estimated annual fuel cost for motor vehicles, with the resulting data provided in the variable annual fuel cost of the Chapter 8 Case Study data set Fuel Efficiency. A sample of the annual fuel cost is provided for 12 vehicles.

Annual fuel cost
1750 2500 2400 2350
2150 3100 2950 2500
2550 2750 2300 2800

Question 8.166

69. Construct a normal probability plot of the data (see pages 381–384). Evaluate the normality assumption using the accompanying histogram. Is it appropriate to construct a interval using this data set? Why or why not?

8.2.69

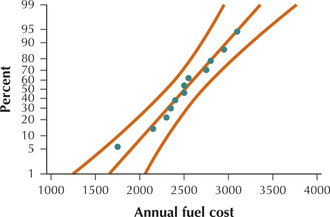
image

Acceptable normality.

Question 8.167

70. Find the point estimate of , the population mean annual fuel cost.

Question 8.168

71. Compute the sample standard deviation .

8.2.71

Question 8.169

72. Find for a confidence interval with 90% confidence.

Question 8.170

73. Construct and interpret a 90% confidence interval for the population mean annual fuel cost.

8.2.73

(2318.2, 2697.8). We are 90% confident that μ, the population mean annual fuel cost, lies between $2318.2 and $2697.8.

Question 8.171

74. Compute and interpret the margin of error for a confidence interval with 90% confidence. What is the meaning of this number?

WORKING WITH LARGE DATA SETS

image Chapter 8 Case Study: Motor Vehicle Fuel Efficiency.

Open the Chapter 8 Case Study data set Fuel Efficiency. Here, we will examine confidence intervals for the population mean amount of carbon dioxide generated by motor vehicles in city driving. We will then see whether these confidence intervals succeeded in capturing the population mean amount of carbon dioxide. Use technology to do the following: image fueleffciency

Question 8.172

75. Obtain a random sample of size 100 from the data set.

8.2.75

Answers will vary.

Question 8.173

76. Suppose we are interested in constructing a 95% interval for the population mean amount of carbon dioxide generated by these vehicles in city driving (the variable city CO2), using our sample from the previous exercise. Do we need to check for normality?

Question 8.174

77. Construct and interpret a 90% interval for the population mean amount of city CO2.

8.2.77

Answers will vary.

Question 8.175

78. Did your interval in Exercise 77 capture the population mean? Check by finding the mean city CO2 of all the vehicles.

Question 8.176

79. Generate a second sample of size 100 from the data set. Construct a second 90% interval for the population mean amount of city CO2. Did this confidence interval capture the population mean?

8.2.79

Answers will vary.

Question 8.177

80. If we keep on obtaining new samples all day long, about what proportion of the 90% confidence intervals will capture the population mean?