Chapter 13 Exercises
Chapter 13 Exercises
13.1 The Adjusted Winner Procedure
Question 13.31
1. The 1991 divorce of Ivana and Donald Trump was widely covered in the media. The marital assets included a 45-room mansion in Greenwich, Connecticut; the 118- room Mar-a-Lago mansion in Palm Beach, Florida; an apartment in the Trump Plaza; a 50-room Trump Tower triplex; and just over $1 million in cash and jewelry. Assume that points are assigned as follows:
| Marital Asset | Point Allocations | |
|---|---|---|
| Donald’s Points | Ivana’s Points | |
| Connecticut estate | 10 | 38 |
| Palm Beach mansion | 40 | 20 |
| Trump Plaza apartment | 10 | 30 |
| Trump Tower triplex | 38 | 10 |
| Cash and jewelry | 2 | 2 |
Use the adjusted winner procedure to determine a fair allocation of the marital assets. (Exercise 1 courtesy of Catherine Duran.)
1.
Donald receives the Trump Tower triplex and about 87% ownership of the Palm Beach mansion. Ivana gets the rest.
Question 13.32
2. Suppose that Calvin and Hobbes discover a sunken pirate ship and must divide their loot. They assign points to the items as follows:
| Object | Calvin’s Points | Hobbes’s Points |
|---|---|---|
| Cannon | 10 | 5 |
| Anchor | 10 | 20 |
| Unopened chest | 15 | 20 |
| Doubloon | 11 | 14 |
| Figurehead | 20 | 30 |
| Sword | 15 | 6 |
| Cannon ball | 5 | 1 |
| Wooden leg | 2 | 1 |
| Flag | 10 | 2 |
| Crow’s nest | 2 | 1 |
Use the adjusted winner procedure to determine a fair allocation of the loot. (Exercise 2 courtesy of Erica DeCarlo.)
Question 13.33
3. This exercise illustrates how the adjusted winner procedure can be used to resolve disputes as well as to achieve fair allocations. Suppose that Mike and Phil are roommates in college, and they encounter serious conflicts during their first week at school. Their resident adviser decides to use the adjusted winner procedure to resolve the dispute. The issues agreed upon, and the (independently assigned) points, turn out to be the following:
| Issue | Mike’s Points | Phil’s Points |
|---|---|---|
| Stereo level | 4 | 22 |
| Smoking rights | 10 | 20 |
| Room party policy | 50 | 25 |
| Cleanliness | 6 | 3 |
| Alcohol use | 15 | 15 |
| Phone time | 1 | 8 |
| Lights-out time | 10 | 2 |
| Visitor policy | 4 | 5 |
Use the adjusted winner procedure to resolve this dispute. (Exercise 3 courtesy of Erica DeCarlo.)
3.
Phil gets his way on the stereo level issue, the smoking rights issue, the phone time issue, the visitor policy issue, and about 87% of his way on the alcohol issue. Mike gets his way on the rest.
Question 13.34
4. Suppose that a labor union and management are trying to resolve a dispute that involves four issues: the base salary of the workers, the annual salary increase that workers can expect, the benefits package the workers will receive, and the amount of vacation time to which each worker will be entitled. Use the adjusted winner procedure to resolve this dispute, with the following point assignments:
| Issue | Labor | Management |
|---|---|---|
| Base salary | 30 | 50 |
| Salary increases | 20 | 40 |
| Benefits | 35 | 5 |
| Vacation time | 15 | 5 |
Question 13.35
5. Mary and Fred are serving as co-chairs of the mathematics department. There are a number of time-consuming tasks that must be done by one or the other. It really doesn’t matter who does which task, except that they disagree on how unpleasant particular tasks are. They decide to use the adjusted winner procedure by phrasing items as “The other co-chair will handle __________________.” The items and point assignments are as follows:
| The other co-chair will handle: | Mary’s Points | Fred’s Points |
|---|---|---|
| Salary recommendations | 11 | 19 |
| Class schedules | 19 | 9 |
| Hiring | 14 | 20 |
| Department meetings | 20 | 10 |
| Calculus placement | 21 | 11 |
| External review | 15 | 31 |
- Which tasks will Mary do?
- Which tasks will Fred do?
- Which task do they share, and who takes on more of the burden for this task?
5.
(a) Mary will handle salary recommendations and external reviews.
(b) Fred will handle class schedules, department meetings, and calculus placement.
(c) They share hiring. Since Fred retained 1217, Mary will be taking on more of the burden.
Question 13.36
6. Make up an example involving two people and several objects for which the adjusted winner procedure can be used, and then use the adjusted winner procedure to determine a fair division.
Question 13.37
7. Make up an example involving two people and several issues for which the adjusted winner procedure can be used, and then use the adjusted winner procedure to determine a fair resolution of the dispute.
7.
Answers will vary.
Question 13.38
8. Suppose we have three items (X, Y, and Z) and three people (Bob, Carol, and Ted). Assume that each person spreads 100 points over the items (as in the adjusted winner procedure) to indicate the relative worth of each item to that person.
| Item | Bob | Carol | Ted |
|---|---|---|---|
| X | 40 | 30 | 30 |
| Y | 50 | 40 | 30 |
| Z | 10 | 30 | 40 |
For each of the allocations listed below, indicate the following:
- Whether or not it is proportional.
- Whether or not it is envy-free.
- Whether or not it is equitable.
- For the ones that are not Pareto-optimal, another allocation that makes one person better off without making anyone else worse off.
Allocation 1: Bob gets Z, Carol gets Y, and Ted gets X. (This is not Pareto-optimal.)
Allocation 2: Bob gets Y, Carol gets Z, and Ted gets X. (This is not Pareto-optimal.)
Allocation 3: Bob gets X, Y, and Z. (This is Pareto-optimal; explain why.)
Allocation 4: Bob gets Y, Carol gets X, and Ted gets Z. (This is Pareto-optimal.)
Allocation 5: Bob gets X, Carol gets Y, and Ted gets Z. (This is Pareto-optimal.)
13.2 The Knaster Inheritance Procedure
Question 13.39
9. If John bids $28,225 and Mary bids $32,100 on their aging parents’ old classic car, which they no longer drive, how would you reach a fair division?

9.
Mary gets the car and places 32,1002=$16,050 in a kitty. John takes out 28,2252=$14,112.50. The remaining $16,050−$14,112.50=$1937.50 is split equally. The net effect of this is that Mary receives the car and pays John $15,081.25.
Question 13.40
10. John and Mary inherit their parents’ old house and classic car. John bids $28,225 on the car and $55,900 on the house. Mary bids $32,100 on the car and $59,100 on the house. How should they arrive at a fair division?
Question 13.41
11. Can you modify your fair-division procedure in Exercise 10 so that both John and Mary receive one of the two objects while still considering the allocation as fair?
11.
Answers will vary.
Question 13.42
12.
 Describe a fair division for three heirs, A, B, and C, who inherit a house in the city, a small farm, and a valuable sculpture, and who submit sealed bids (in dollars) on these objects as follows:
Describe a fair division for three heirs, A, B, and C, who inherit a house in the city, a small farm, and a valuable sculpture, and who submit sealed bids (in dollars) on these objects as follows:
| A | B | C | |
|---|---|---|---|
| House | $145,000 | $149,999 | $165,000 |
| Farm | $135,000 | $130,001 | $128,000 |
| Sculpture | $110,000 | $80,000 | $127,000 |
13.3 Fair Division and Organ Transplant Policies
Question 13.43
13. Construct the table showing how points would be allocated among the following four potential recipients for a kidney transplant, according to the criteria in Section 13.3.
| Potential Recipient | Months Waiting | Antigens Matched | Percent Sensitized |
|---|---|---|---|
| A | 9 | 2 | 20 |
| B | 6 | 3 | 0 |
| C | 5 | 4 | 40 |
| D | 2 | 6 | 60 |
13.
See table below.
| Potential Recipient | Months Waiting, Position in Terms of Waiting, and Points Awarded | Antigens Matched and Points Awarded | Percent Sensitized and Points Awarded | Total Points |
| A | 9 (1) 10×(44)=10 points |
2 2×2=4 points |
20% 2 points |
16.0 |
| B | 6(2) 10×(34)=7.5 points |
3 2×3=6 points |
0% 0 points |
13.5 |
| C | 5 (3) 10×(24)=5 points |
4 2×4=8 points |
40% 4 points |
17.0 |
| D | 2 (4) 10×(14)=2.5 points |
6 2×6=12 points |
60% 6 points |
20.5 |
Question 13.44
14. Does the example in Exercise 13 give rise to the same kind of paradox as in Section 13.3? Explain why or why not.
13.4 Taking Turns
Question 13.45
15. Suppose that Bob and Carol rank a series of objects, from most preferred to least preferred, as follows:
| Bob | Carol |
|---|---|
| Car | Boat |
| Investments | Investments |
| MP3 player | Car |
| Boat | Washer-dryer |
| Television | Television |
| Washer-dryer | MP3 player |
Assume that Bob and Carol use the bottom-up strategy and that Bob gets to choose first. Determine Bob’s first choice and the final allocation.
15.
Bob first chooses the investments, and the final allocation has him also receiving the car and the MP3 player.
| Potential Recipient | Months Waiting, Position in Terms of Waiting, and Points Awarded | Antigens Matched and Points Awarded | Percent Sensitized and Points Awarded | Total Points |
| A | 9 (1) 10×(44)=10 points |
2 2×2=4 points |
20% 2 points |
16.0 |
| B | 6(2) 10×(34)=7.5 points |
3 2×3=6 points |
0% 0 points |
13.5 |
| C | 5 (3) 10×(24)=5 points |
4 2×4=8 points |
40% 4 points |
17.0 |
| D | 2 (4) 10×(14)=2.5 points |
6 2×6=12 points |
60% 6 points |
20.5 |
Question 13.46
16. Repeat Exercise 15 under the assumption that Carol gets to choose first.
Question 13.47
17. Mark and Fred have inherited a number of items from their parents’ estate, with no indication of who gets what. They rank the items from most preferred to least preferred, as follows:
| Mark | Fred |
|---|---|
| Truck | Boat |
| Tractor | Tractor |
| Boat | Car |
| Car | Truck |
| Tools | Motorcycle |
| Motorcycle | Tools |
Assume that Mark and Fred use the bottom-up strategy and that Mark gets to choose first. Determine Mark’s first choice and the final allocation.
17.
Mark first chooses the tractor, and the final allocation has him also receiving the truck and the tools.
Question 13.48
18. Repeat Exercise 17 under the assumption that Fred gets to choose first.
Question 13.49
19. Suppose that Donald and Ivana Trump decide to settle their divorce (described in Exercise 1 on page 563) by taking turns. Assume that they both use the bottom- up strategy, and Donald chooses first. Determine Donald’s first choice and the final allocation. (Assume that Donald values the Connecticut estate slightly more than he values the Trump Plaza apartment.)
19.
Donald first chooses the Palm Beach mansion, and the final allocation has him also receiving the Trump Tower triplex and the cash and jewelry.
Question 13.50
20. Repeat Exercise 19 under the assumption that Ivana gets to choose first.
13.5 Divide-and-Choose
Question 13.51
21. Suppose that Bob is entitled to one-fourth of a cake and Carol is entitled to three-fourths. In a few sentences, explain how divide-and-choose can be used to achieve an allocation in which each party is guaranteed to receive at least as much as he or she is entitled to.
21.
One way is to have Bob divide the cake into four pieces and to let Carol choose any three. Another is to have Bob divide the cake into two pieces and then let Carol choose one. They can do divide-and-choose on the piece that Carol did not choose.
Question 13.52
22. Suppose that Bob, Carol, and Ted view a cake as having 18 units of value, with each unit of value represented by a small square (as in the accompanying illustration). Suppose, however, that the players value various parts of the cake differently (or that Bob views the cake as being perfectly rectangular, whereas Carol and Ted see it as skewed in opposite ways). We represent this pictorially as follows:
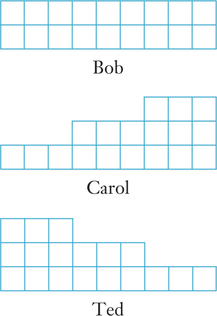
Assume that all cuts that will be made are vertical.
- If Bob and Carol use divide-and-choose to divide the cake between them, how large a piece will each receive (assuming they follow the suggested strategies that go with divide-and-choose and that Bob is the divider)?
- If Carol and Ted use divide-and-choose to divide the cake between them, how large a piece will each receive (assuming that they follow the suggested strategies that go with divide-and-choose and that Carol is the divider)?
Question 13.53
23. Assume that Bob and Carol view the cake as in Exercise 22, but assume also that each knows how the other values the cake, and that neither is spiteful. Suppose they are to divide the cake using the rules, but not necessarily the strategies, of divide-and-choose. Is Bob better off being the divider or the chooser?
23.
Bob should be the divider. That way, he can get 12 units of value instead of 9 units of value.
13.6 Cake-Division Procedures: Proportionality
Question 13.54
24. Suppose that Players 1, 2, and 3 view a cake as in Exercise 22. Notice that each player views the cake as having 18 square units of area (or value). Assume that each player regards a piece as acceptable if and only if it is at least 18/3=6 square units of area (his or her “fair share”). Assume also that all cuts made correspond to vertical lines.

- Provide three drawings to show how each player views a division of the cake by Player 1 into three pieces he or she considers to be the same size or value. Label the pieces A, B, and C.
- Identify two of these pieces that Player 2 finds acceptable and two that Player 3 finds acceptable.
- Show that a feasible assignment of fair pieces can be achieved by letting the players choose in the following order: Player 3, Player 2, Player 1. Indicate how many square units of value each player thinks he or she received. Is there any other order in which players can choose pieces (in this example) that also results in a feasible assignment?
Question 13.55
25. Suppose that Players 1, 2, and 3 view a cake as follows:
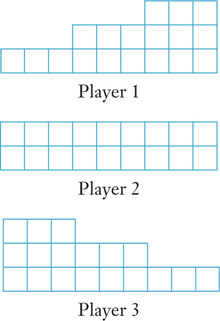
- Provide three drawings to show how each player views a division of the cake by Player 1 into three pieces that he or she considers to be the same size or value. Label the pieces A, B, and C. (We are still assuming that all cuts correspond to vertical lines, so this will require a cut along a vertical center line of some of the squares.)
- Show that neither Player 2 nor Player 3 finds more than one of the three pieces acceptable (with “acceptable” defined as in Exercise 24).
- Identify a single piece that Player 2 and Player 3 agree is not acceptable. (There are actually two such pieces; for definiteness, find the one on the right.)
- Assume that Players 2 and 3 give the piece from part (c) to Player 1, and that they reassemble the rest and Players 2 and 3 divide it between themselves using divide-and-choose (with a single vertical cut). Determine what size piece each of the three players will think he or she received (i) if Player 2 divides and Player 3 chooses, and (ii) if Player 3 divides and Player 2 chooses.
25.
(a) See figures below.
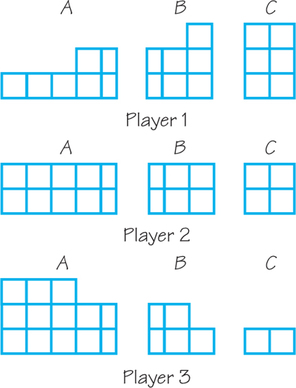
(b) Player 2 finds A acceptable (9 square units), but not B (5 square units) or C (4 square units). Player 3 finds A acceptable (12 square units), but not B (4 square units) or C (2 square units).
(c) Players 2 and 3 both find B and C unacceptable.
( C is on the right.)
(d) (i) Player 1 gets a piece he thinks is 6 square units. Player 2 gets a piece he thinks is 7 square units, and Player 3 gets a piece he thinks is 10 square units.
(ii) Player 1 gets a piece she thinks is 6 square units, Player 2 gets a piece she thinks is 823 square units, and Player 3 gets a piece she thinks is 8 square units.
Question 13.56
26. Suppose Players 1, 2, and 3 view a cake as in Exercise 25. Illustrate the last-diminisher method (still restricting attention to vertical cuts and, in addition, assuming that the piece potentially being diminished is a piece off the left side of the cake) by following steps (a) through (f) below.
- Draw a picture showing the third of the cake (6 squares) that Player 1 will slice off the cake.
- Determine whether Player 2 will pass or further diminish this piece. If he or she would further diminish it, make a new drawing.
- Determine whether Player 3 will pass or further diminish this piece. If he or she would further diminish it, make a new drawing.
- Determine who receives the piece cut off the cake and what size or value he or she thinks it is. (Actually, we knew what size the person receiving this first piece would think it was, assuming that he or she followed the prescribed strategy. How did we know this?)
- Finish the last-diminisher method using divide- and-choose on what remains, with the lowest-numbered player who remains doing the dividing.
- Redo step (e) with the other player doing the dividing.
Question 13.57
27. The Banach-Knaster last-diminisher method is not the only well-known cake-division procedure that yields a proportional allocation for any number of players. There is also one due to A. M. Fink (sometimes called the lone-chooser method). For three players (Bob, Carol, and Ted), it works as follows:
- Bob and Carol divide the cake into two pieces using divide-and-choose.
- Bob now divides the piece he has into three parts that he considers to be the same size. Carol does the same with the piece she has.
- Ted now chooses whichever of Bob’s three pieces that he (Ted) thinks is largest, and Ted chooses whichever of Carol’s three pieces that he thinks is largest.
- Bob keeps his remaining two pieces, as does Carol.
- Explain why Ted thinks he is getting at least one-third of the cake.
- Explain why Bob and Carol each think they are receiving at least one-third of the cake.
- Explain why, in general, this scheme is not envy-free.
27.
(a) Ted thinks he is getting at least one-third of the piece that Bob initially received and at least one- third of the piece that Carol initially received. Thus, Ted thinks he is getting at least one-third of part of the cake (Bob’s piece) plus one-third of the rest of the cake (Carol’s piece).
(b) Bob gets to keep exactly two-thirds (in his own view) of the piece that he initially received and thought was at least of size one-half. Two-thirds times one-half equals one-third. The same argument applies to Carol.
(c) If, for example, Ted thinks the half Carol initially gets is worthless, then Ted may wind up thinking that he (Ted) has only slightly more than one-third of the cake, while Bob has (in Ted’s view) almost two-thirds of the cake. In such a case, Ted will envy Bob.
Question 13.58
28. In A. M. Fink’s procedure (described in Exercise 27), suppose that a fourth person (Alice) comes along after Bob, Carol, and Ted have already divided the cake among themselves so that each of the three thinks that he or she has a piece of size at least one-third. Mimic what was done in the three-person case to obtain an allocation among the four that is proportional. (Hint: Begin by having Bob, Carol, and Ted divide the pieces they have into a certain number—how many?—of equal parts.)
13.7 Cake-Division Procedures: The Problem of Envy
Question 13.59
29. Suppose Players 1, 2, and 3 view the cake as in Exercise 25. Illustrate the envy-free procedure for n=3 (yielding an allocation of part of the cake) by following steps (a) through (c) below. Again, restrict attention to vertical cuts.
- Provide a total of three drawings to show how each player views a division of the cake by Player 1 into three pieces he or she considers to be the same size or value. Label the pieces A, B, and C. (This is the same as Exercise 25a.)
- Redraw the picture from Player 2’s view, and illustrate the trimming of piece A that he or she would do. Label the trimmed piece A and the actual trimmings T.
- Indicate which piece each player would choose (and what he or she thinks its size is) if the players choose in the following order, according to the envy-free procedure: Player 3, Player 2, Player 1.
29.
(a) See figures below.
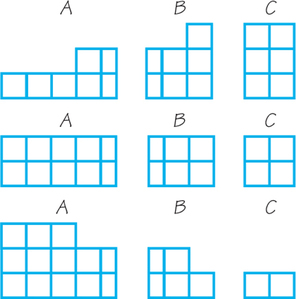
(b) See figures below.
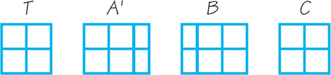
(c) Player 3 will choose A (which he thinks is of size 6 square units). Player 2 will choose B (which he thinks is of size 5 square units). Player 1 will receive C (which he thinks is of size 6 square units). The proviso does not come into play (since Player 3 took the trimmed piece).
Question 13.60
30. There is a two-person moving-knife cake-division procedure due to A. K. Austin that leads to each player receiving a piece of cake that he or she considers to be of size exactly one-half. It begins by having one of the two players (Bob) place two knives over the cake, one of which is at the left edge and the other of which is parallel to the first and placed so that the piece between the knives (A in the picture below) is of size exactly one-half in Bob’s estimation.
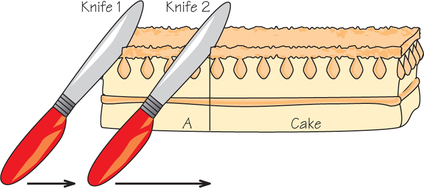
If Carol agrees that this is a 50-50 division, we are done. Otherwise, Bob starts moving both knives to the right—perhaps at different rates—so that the piece between the knives remains of size one-half in his eyes. Carol calls “stop” at the point when she also thinks the piece between the two knives is of size exactly one-half.
- If the knife on the right were to reach the right-hand edge, where would the knife on the left be?
- Explain why there definitely is a point where Carol thinks the piece between the two knives is of size exactly one-half. (Hint: If Carol thinks the piece is too small at the beginning, what will she think of it at the end?)
Question 13.61
31. Here are the steps in the Selfridge-Conway procedure for three players.
Stage 1. The initial division
- Step 1. Player 1 cuts the cake into, what in his view, is three equal pieces.
- Step 2. Player 2, if he thinks one piece is largest, trims from that piece to create what he believes is a two-way tie for largest piece. The trimmings are set aside. If Player 2 thinks that the original split was fair, he does nothing.
- Step 3. Player 3 may choose any piece.
- Step 4. Player 2 chooses a piece. If the trimmed piece remains, he must choose it. If not, he chooses the one he feels is tied with the trimmed piece for largest.
- Step 5. Player 1 gets the remaining piece.
Stage 2. Dividing the trimmings
Assume that Player 3 received the trimmed piece in Stage 1.
- Step 6. Player 2 divides the trimmings into what he considers three equal parts.
- Step 7. Player 3 chooses one part of the trimmings.
- Step 8. Player 1 chooses a piece of the trimmings.
- Step 9. Player 2 receives the remaining trimmings.
- Explain why Player 1 is envy-free after Stage 1.
- Explain why Player 2 is envy-free after Stage 1.
- Explain why Player 3 is envy-free after Stage 1.
- Explain why Player 1 is envy-free after Stage 2.
- Explain why Player 2 is envy-free after Stage 2.
- Explain why Player 3 is envy-free after Stage 2.
(Thanks to Michael Rosenthal for suggesting this exercise topic.)
31.
(a) This is because Player 1 views all three pieces as being of equal size or value.
(b) Player 2 created a two-way tie for largest or most valuable piece. Player 3 may take one of these, but at least one will still be available for Player 2 to choose.
(c) This is because Player 3 gets to choose first.
(d) Player 1 will not envy Player 3 because Player 3 received the trimmed piece, and so Player I’s piece is as large in his eyes as Player 3’s piece plus all of the trimmings. Player 1 will not envy Player 2 because he is choosing before Player 2.
(e) This is because Player 2 views all three pieces of the trimmings as being of equal size or value.
(f) This is because Player 3 gets to choose first.
13.8 Vickrey Auctions
Question 13.62
32. Consider the Vickrey auction for a lamp that is worth $100 to our bidder Bob (page 559). Suppose someone suggests that Bob would always do as well with a bid of $80. Show that this is false by playing the role of another bidder who could make Bob regret a choice of bidding $80 rather than his (sincere) bid of $100. You are free to make any assumptions that you want about the bids other than Bob’s and your own.
Question 13.63
33. Consider the Vickrey auction for a lamp that is worth $100 to our bidder Bob (page 559). Suppose someone suggests that Bob would always do as well with a bid of $120. Show that this is false by playing the role of another bidder who could make Bob regret a choice of bidding $120 rather than his (sincere) bid of $100. You are free to make any assumptions you want about the bids other than Bob’s and your own.
33.
If I bid, say, $110, then Bob wins the lamp but pays $10 more than he thinks it’s worth. This is worse for him than bidding $100 and losing the auction.
Chapter Review
Question 13.64
34. Beth and Harvey are co-captains of their intramural softball team. As in Exercise 5 (page 564), there are a number of time-consuming tasks that must be done by one or the other. It really doesn’t matter who does which task, except that they disagree on how unpleasant particular tasks are. Like Fred and Mary, Beth and Harvey decide to use the adjusted winner procedure by phrasing items as “The other co-chair will handle _____________.” The items and point assignments are as follows:
| The other co-chair will handle: | Beth’s Points | Harvey’s Points |
|---|---|---|
| Selection of player positions | 9 | 40 |
| Coordination of game schedule | 9 | 10 |
| Reserving the field | 9 | 11 |
| Scheduling practices | 9 | 12 |
| Checking equipment | 9 | 13 |
| Planning the end-of-season party | 55 | 14 |
- Which tasks will Beth do?
- Which tasks will Harvey do?
- Which task do they share, and who takes on more of the burden for this task?
Question 13.65
35. Describe a fair division for three children, E, F, and G, who inherit equal shares of their parents’ classic car collection and who submit sealed bids (in dollars) on these five cars as follows:
| E | F | G | |
|---|---|---|---|
| Duesenberg | $18,000 | $15,000 | $15,000 |
| Bentley | $18,000 | $24,000 | $20,000 |
| Ferrari | $16,000 | $12,000 | $16,500 |
| Pierce-Arrow | $14,000 | $15,000 | $13,500 |
| Cord | $24,000 | $18,000 | $22,000 |
35.
For the final resolution, E receives the Duesenberg and Cord and pays $8500, F receives the Bentley and Pierce-Arrow and pays $7500, and G receives the Ferrari plus $16,000.
Question 13.66
36. In the scheme for arriving at a priority ranking for organ transplants, how might one change the way points are assigned for “waiting time” so that the kind of paradox that arose in Section 13.3 could not occur?
Question 13.67
37. Suppose that Mary and Fred decide to settle the question of which co-chair performs which tasks (described in Exercise 5 on page 564) by taking turns. Assume that they both use the bottom-up strategy, and Mary chooses first. Determine the final allocation of tasks.
37.
Fred will do the calculus placement, department meetings, and class schedules. Mary will do external reviews, hiring, and salary recommendations.
Question 13.68
38. Repeat Exercise 37 under the assumption that Fred chooses first.
Question 13.69
39. If you and another person are using the divide-and-choose procedure to divide something between you, would you rather be the divider or the chooser? (Assume that neither of you knows anything about the preferences of the other.)
39.
It is better to be the chooser. As divider, I’d get exactly 50% (or risk getting less). As chooser, I have a guarantee of getting at least 50% and the possibility (depending on the division) of getting more than 50%.
Question 13.70
40. There is a moving-knife version of the Banach- Knaster procedure that is due to Dubins and Spanier. To describe it, we picture the cake as being rectangular and the procedure beginning with a referee holding a knife along the left edge, as illustrated below.
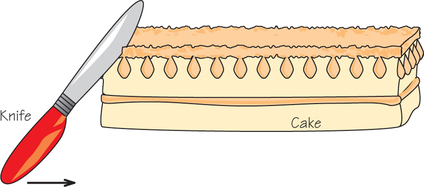
Assume, for the sake of illustration, that there are four players (Bob, Carol, Ted, and Alice). The referee starts moving the knife from left to right over the cake (keeping it parallel to the position in which it started) until one of the players (assume it is Bob) calls “cut.” At this time, a cut is made, the piece to the left of the knife is given to Bob, and he exits the game. The knife starts moving again, and the process continues. The strategies are for each player to call “cut” whenever it would yield him or her a piece of size at least one-fourth.
- Explain why this procedure produces an allocation that is proportional.
- Explain why the resulting allocation is not, in general, envy-free.
- Explain why, if you are not the first player to call “cut,” there is a strategy different from the one suggested that is never worse for you, and sometimes better.