15.5 15.4 Mechanism Design and Larger Games
We have shown how to compute optimal pure and mixed strategies, and the values ensured by using them, in 2×2 constant-sum games. In 2×2 variable-sum games, we focused on Nash equilibria as a solution concept in the Prisoners’ Dilemma and Chicken, but we found that this notion of a stable outcome did not justify the choice of cooperative strategies in either of these games.
We turn next to a game in which there may be any number of players, each of whom can choose among an infinite number of strategies! Although this game sounds more complex, it demonstrates that it may be easy to determine a Nash equilibrium, and it may be easy for each player to determine an optimal strategy.
The game models a specific type of auction. An auction is a common way to sell an item when the seller is unsure of the going price of the item; the auction is designed to get the seller the highest price for the item. For example, Sotheby’s auction house specializes in high-end contemporary art and rare items such as the British Guiana one-cent magenta stamp, considered the rarest and most valuable stamp in the world. Because these items are one of a kind, the seller has difficulties in knowing what the market value for the item is. Auctions have become more common as websites like eBay hold auctions in which bidders can participate online at any hour of the day. Stamp collectors had used the following type of auction well before Columbia University economist William Vickrey analyzed it formally in 1961.
A Vickrey Auction DEFINITION
In a Vickrey auction, also called the second-price sealed-bid auction, bidders independently submit sealed bids for an item being sold. The winner is the one who bids the highest, but he or she pays only the amount of the second-highest bid.
A Vickrey auction involves a bidding strategy that is at least as good as any other. This notion weakens the idea of a dominant strategy that was introduced when analyzing the Prisoners’ Dilemma. A weakly dominant strategy is one that is at least as good as any other strategy. Flipping perspective, we define a dominated strategy.
Dominated Strategy DEFINITION
A player’s strategy S is dominated by his or her strategy T if the outcome under T is always better for the player than the outcome under S, regardless of the decisions made by the other players.
In the location/schedule game of Example 1 with payoff matrix from Table 15.1 (page 623), Mark chooses the location of the hospital, while Lisa chooses the shift. Recall that Mark is concerned about making the highest hourly wage possible for his emergency room work. For this reason, Mark will never select the Rural hospital because he would receive a lower hourly wage than he would at the Suburban hospital, regardless of which shift Lisa selects. This is apparent because the numbers in the Suburban row of Table 15.1 are greater than the numbers in the Rural row. We say that the Rural strategy is dominated by the Suburban strategy.
Dominated strategies can be eliminated from consideration, as there will never be a situation in which a dominated strategy should be played.
EXAMPLE 9 The Vickrey Auction
The Vickrey Auction
Suppose that Anneliese, Binh, and Charlie bid for a stamp in a Vickrey auction. Anneliese, Binh, and Charlie value the stamp at $300, $200, and $100, respectively. To see that it is always at least as good for Anneliese to bid her true valuation of the stamp, consider the two possible results of bidding $300. To simplify the analysis, we will assume that each bidder’s bid is distinct, so no two bidders bid the same amount.
- If Anneliese’s bid of $300 is the highest bid, then she wins the item but pays the second-highest bid $SH, which is strictly less than $300. To represent the Vickrey auction as a game, Anneliese’s payoff in this case is given by $300−$SH, which is a positive number because Anneliese was able to buy the stamp for less than she valued it. If she had decided to bid more than $300, then she would still be the highest bidder and still pay the same amount $SH. However, if she decides to bid less than $300, then it is possible that her bid will be less than $SH, in which case she loses the item and has a payoff of $0. Anneliese has no incentive to raise or to lower her bid because she can do no better than a payoff of $300−$SH, but she can do worse, receiving a payoff of $0 if she bids too low.
- If Anneliese’s bid of $300 is not the highest bid, then she does not receive the item, and naturally does not have to pay for it—she receives a payoff of $0. Let $H be the highest bid. If she had decided to bid more than $300, say, more than $H, then she becomes the highest bidder and would have had to pay $H, which is more than $300—the value she placed on the stamp. This means that she would have overpaid for the stamp and her payoff would be the negative amount of $300−$SH. If she bids less than $300, she would still fail to have the highest bid and would still not have to pay anything. As before, Anneliese has no incentive to raise or to lower her bid.
Anneliese’s strategy of bidding $300 weakly dominates any other strategy she could use. A similar analysis holds for Binh and Charlie. Collectively, it is a Nash equilibrium for Anneliese, Binh, and Charlie to each bid his or her true valuation for the stamp. To see this, if Anneliese, Binh, and Charlie bid $300, $200, and $100, respectively, for the stamp, then Anneliese will be the highest bidder and pay $200 for the stamp. The payoffs for Anneliese, Binh, and Charlie are given by the triplet ($300−$200=$100,$0,$0). Neither Binh nor Charlie could change his bid to receive a positive payoff. Anneliese’s bid cannot affect the price she pays; it can determine only whether or not she is the highest bidder. Likewise, she cannot change her bid to do better and could only do worse by bidding too little and losing the stamp to Binh.
If more than one player has the highest bid, then one of the players is selected at random to receive the item and the second highest bid is equal to the highest bid. The analysis in the example extends for a Vickrey auction with any number of players. Each player has a weakly dominant strategy to bid his or her true valuation of the item. It leads to the following result.
Nash Equilibrium in a Vickrey Auction THEOREM
In a Vickrey auction, it is a Nash equilibrium for each bidder to bid the amount at which he or she values the item.
The Vickrey auction induces the bidders to reveal truthfully their values for the item being auctioned (see Chapter 13, Section 13.8, for more on Vickrey auctions). However, there are other equilbria for the Vickrey auction game. For the stamp auction, bids of $201, $200, and $100 and of $200, $301, and $100 by Anneliese, Binh, and Charlie, respectively, are also Nash equilibria. The second of these two equilibria is surprising because Binh can win the item! For games in which each player has a dominant strategy (like the Prisoners’ Dilemma), then there is a single Nash equilibrium. It is also a Nash equilibrium for every player to use a weakly dominant strategy, but there may be more than one equilibrium if each player has a weakly dominant strategy, as demonstrated by the Vickrey auction game.
Self Check 7
Suppose Anneliese, Binh, and Charlie bid $150, $301, and $100, respectively, at the stamp auction. Why does Anneliese not prefer to change her bid? Why does Binh prefer not to change his bid? Does your answer to the question about Anneliese also hold for Charlie? Answering these three questions shows that when Anneliese, Binh, and Charlie bid as described, it is a Nash equilibrium: Collectively, if no player wishes to change his or her bid, the bids form a Nash equilibrium.
When Anneliese, Binh, and Charlie have bids of $150, $301, and $100, respectively, then Binh gets the item, pays $150 (the second highest bid), and achieves a $200−$150=$50 payoff. Because Anneliese and Charlie don’t get the item and don’t pay anything, each receives a payoff of 0.
If Anneliese bids anything less than $301, then she will not get the item; this means that she has a payoff of 0. If she bids $301 or more, then she could receive the item and pay more than what it is worth to her. This is a negative payoff. Because she cannot increase her payoff, she has no desire to change her bid. Binh already gets the item, so bids above $150 do not change who gets the item or how much Binh pays. If Binh bids less than $150, then he doesn’t get the item and his payoff is 0. Binh doesn’t wish to risk bidding $150 and possibly not getting the item. Binh has no incentive to change his bid. Like Anneliese, if Charlie bids more than $301, he will win the stamp but pay too much for it. This result could occur if he bids $301, too. For bids less than $301, Charlie still doesn’t get the item and pays nothing. Charlie has no reason to change his bid, either.
Mechanism design is the act of designing a game to achieve a particular outcome as a Nash equilibrium. Despite the multiple equilibria for the Vickrey auction game, the Vickrey auction does give each bidder an incentive to reveal truthfully how much he or she values the item. Another example of mechanism design is the design of matching markets, described in Spotlight 15.2. Similar objectives border on the intersection of economics and psychology, in which decision problems are posed in a particular way to encourage people to make better decisions. For example, the placement of healthy food by a checkout register in a school’s lunchroom results in more healthy choices by students.
The Nobel Prize in Economics 15.2
15.2
The Nobel Memorial Prize in Economics was awarded to three game theorists in 1994, marking the 50th anniversary of the publication of the first text on game theory (Theory of Games and Economic Behavior) by mathematician John von Neumann and economist Oskar Morgenstern.
- John C. Harsanyi (1920–2000) of the University of California, Berkeley, a Hungarian-American who emigrated from Hungary to Australia in 1950 and then to the United States in 1956. He is well known for extending game theory to the study of ethics and showing how societal institutions, each of whose members’ satisfaction can be measured against that of others, choose among alternatives. His other major contribution was to give a precise definition to “incomplete information” in games in which players may be thought of as different types, and probabilities are assigned to each type.
- John F. Nash, Jr. (1928-2015) of Princeton University, an American mathematician who did pathbreaking work on both noncooperative game theory (the Nash equilibrium is named after him) and cooperative game theory, especially on bargaining, in which axioms or assumptions are specified and a unique solution that satisfies these axioms is derived. Nash obtained his results in the early 1950s, when he was only in his 20s, after which he became mentally ill and was unable to work. Fortunately, he made a remarkable recovery and resumed research until he was killed in a car accident.
- Reinhard Selten (b. 1930) of the University of Bonn, a German mathematician who proposed significant refinements in the concept of the Nash equilibrium that help to distinguish those that are most plausible in games (often there are many such equilibria, which creates a selection problem). Selten is also noted for pioneering work on developing game-theoretic models in evolutionary biology.



In 2005, mathematician Robert J. Aumann was awarded the prize for a variety of advances in cooperative and noncooperative game theory, and economist Thomas C. Schelling also was awarded the prize for his contributions to the study of conflicts involving promises, threats, and other kinds of commitments. Mathematician Lloyd Shapley and economist Alvin Roth were awarded the 2012 Nobel Prize for their application of game theory to the design of markets (see the Case Study at the end of Part I, page 174). Highly successful implementations of these types of matching markets include “The Match,” in which physicians are paired up with residency programs, and school choice, in which students are enrolled in schools across Boston and New York based on different criteria.
Because the bidders could bid any amount, it was not practical to use a payoff matrix to describe the Vickrey auction game. However, for two-player games, we have used payoff matrices to describe games in strategic form. In these games, the row and column players’ choices of strategies led to an outcome from which each player received a payoff. These strategy choices were assumed to be simultaneous, though mentally the players might eliminate some dominated strategies. This was the case of the schedule/location game from Example 1, as Mark would never select the Rural hospital.
In the next example, which involves a larger game, we start by assuming simultaneous choices and show what outcome would occur. Then we assume that the choices of the players need not be simultaneous, instead allowing for one player to move first. We use a game tree to analyze the sequential choices players can then make, as occurs when first you move, then I move, and so on—which are called games in extensive form. As we will see, the outcome in such a game may be wholly different from the outcome in a game with simultaneous choices, which raises the question of which kind of game is the most realistic model of a situation.
EXAMPLE 10 A Truel
A Truel
A truel is like a duel, except that there are three players. Truels are depicted in several movies, including The Good, the Bad and the Ugly (1966), Reservoir Dogs (1992), and Pulp Fiction (1994). The photo below shows three of the characters in The Good, the Bad and the Ugly, about to engage in a truel—each man is armed and planning his next move.

In a truel, each player can either fire or not fire his or her gun at either of the other two players. We assume the goal of each player is, first, to survive and, second, to survive with as few other players as possible. Each player has one bullet and is a perfect shot; no communication (e.g., to pick out a common target) leading to a binding agreement with other players is allowed, making the game noncooperative. We will discuss the answers that simultaneous choices, on the one hand, and sequential choices, on the other, give to what is optimal for the players to do in the truel.
If choices are simultaneous, at the start of play, each player will fire at one of the other two players, killing that player.
Why will the players all fire at each other? Because their own survival does not depend an iota on what they do. Since they cannot affect what happens to themselves but can affect how many others survive (the fewer the better, according to the postulated secondary goal), they should all blaze away at each other. In fact, the players all have dominant strategies to shoot at each other because whether or not a player survives—we will discuss shortly the probabilities of doing so—he or she does at least as well shooting an opponent.
The game, and optimal strategies in it, would change if the players (1) were allowed more options, such as to fire in the air and thereby disarm themselves, or (2) did not have to choose simultaneously but, instead, a particular order of play were specified. Thus, if the order of play were A, followed by B and C choosing simultaneously, followed by any player with a bullet remaining choosing, then A would fire in the air, and B and C would subsequently shoot each other. (A is no threat to B or C, so neither of the latter will fire at A and waste a bullet; on the other hand, if one of B or C did not fire immediately at the other, that player would not survive to get in the last shot, so both B and C will fire at each other.) Thus, A will be the sole survivor.
In 1992, a modified version of this scenario was played out in late-night television programming among the three major TV broadcasting networks of the time, with ABC effectively going first with Nightline, its well-established news program, and CBS and NBC dueling about which host, David Letterman or Jay Leno, to choose for their entertainment shows. Regardless of their ultimate choices, ABC “won” when CBS and NBC were forced to divide the entertainment audience. In 2002, ABC, presumably to attract a younger audience than the one that watched Nightline, attempted unsuccessfully to hire Letterman from CBS. Ted Koppel retired in 2005, but Nightline continues with other hosts.
To return to the original game (all choose simultaneously), the players’ strategies of all firing have two possible consequences: Either one player survives (even if two players fire at the same person, the third must fire at one of them, leaving only one survivor), or no player survives (if each player fires at a different person). In either event, there is no guarantee of survival. In fact, if each player has an equal probability of firing at one of the two other players, the probability that any player will survive is only 25%. The reason is that if the three players are A, B, and C, A will be killed if B fires at him or her, C does, or both do. The only circumstance in which A will survive is if B and C fire at each other, which gives A 1 chance in 4.
If choices are sequential, no player will fire at any other, so all will survive.
At the start of the truel, all the players are alive, which satisfies their primary goal of survival, though not their secondary goal of surviving with as few others as possible. Now assume that A contemplates shooting B, thereby reducing the number of survivors. Looking ahead, however, A knows that by firing first and killing B, he or she will be defenseless and be immediately shot by C, who will then be the sole survivor.
It is in A’s interest, therefore, not to shoot anybody at the start, and the same logic applies to each of the other players. Hence, everybody will survive, which is a happier outcome than when choices are simultaneous, in which case everyone’s primary goal of survival is not satisfied—or, quantitatively speaking, satisfied only 25% of the time.
While sequential choices produce a “happier” outcome, do they provide a plausible model of a strategic situation that mimics what people might actually think and do in such a situation? We believe that the players in the truel, artificial as this kind of shootout may seem, would be motivated to think ahead, given the dire consequences of their actions. Therefore, they would hold their fire, knowing that if one fired first, he or she would be the next target. Indeed, this truel scenario is parodied in “Stand Off,” a Saturday Night Live skit broadcast on November 17, 2012, in which the three characters go about a day in their lives with guns trained on one another and no one wanting to fire first.
In Figure 15.4, we show this logic somewhat more formally with a game tree, in which A has three strategies, as indicated by the three branches that sprout from A: not shoot (ˉS), shoot B, or shoot C. The latter two branches, in turn, give survivors C and B, respectively, two strategies: not shoot (ˉS) or shoot A.
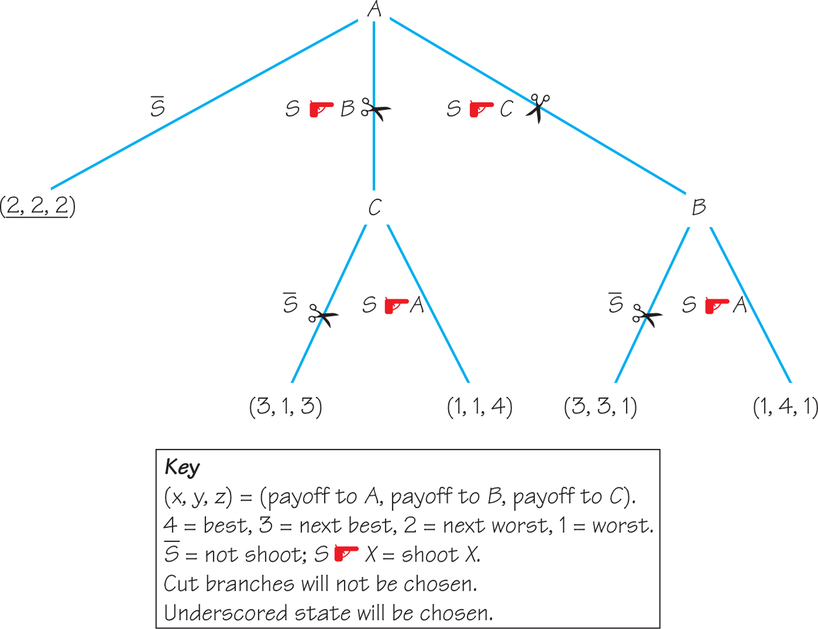
We assume that the players rank the outcomes as follows, which is consistent with their primary and secondary goals: 4 = best (lone survivor), 3 = next best (survivor with one other), 2 = next worst (survivor with two others), and 1 = worst (nonsurvivor). These payoffs are given for ordered triples (A, B, C); thus, (3, 3, 1) indicates the next-best payoffs for A and B and the worst payoff for C.
Note that play necessarily terminates when there is only one survivor, as is the case at (1, 1, 4) and (1, 4, 1). To keep the tree simple, we assume that play also terminates when either A initially chooses ˉS, or B or C subsequently chooses ˉS, giving outcomes of (2, 2, 2), (3, 3, 1), and (3, 1, 3), respectively. Of course, we could allow the two or three surviving players in the latter cases to make subsequent choices in an extended game tree, but this example is meant only to illustrate the analysis of a game tree, not to be the definitive statement on truel possibilities. (More will be explored in the exercises.)
In a game in extensive form represented by a game tree, players work backward, starting the analysis at the bottom of the tree. By “bottom” we mean where play terminates; because this is where the tree branches out, the tree looks upside down in Figure 15.4. The players then work up the tree, using backward induction. Backward induction is a reasoning process in which players, working backward from the last possible moves in a game, anticipate each other’s rational choices.
To illustrate, because C prefers (1, 1, 4) to (3, 1, 3), we indicate that C would not choose ˉS by “cutting” this branch with scissors. Similarly, B would not choose ˉS. Thus, if play got to the bottom of the tree, C would shoot A if C were the survivor, and B would shoot A if B were the survivor, following A’s shooting C or B, respectively.
Moving up to the next level, A would know that if he or she shot B, (1, 1, 4) would be the outcome. If he or she shot C, (1, 4, 1) would be the outcome, making one or the other the outcome from the bottom level. Choosing between these two outcomes and (2, 2, 2), A would prefer the latter, so A would cut the two branches, S would shoot B, and S would shoot C. Hence, A would choose ˉS, terminating play with nobody shooting anybody else.
This, of course, is the conclusion that we reached earlier, based on the reasoning that if A shot either B or C, he or she would end up dead, too. Because we could allow each player, like A, to choose among his or her three initial strategies in a 3×3×3 game, and subsequently make moves and countermoves from the initial state (if feasible), the foregoing analysis applies to all players.
Self Check 8
Use backward induction to determine how players A and B would make their sequential decisions for the game tree in Figure 15.5.
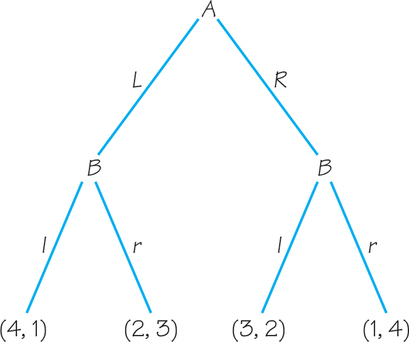
- Player B would play r for both of his decision nodes. For the left node, B prefers r to l because rgives 3 as opposed to 1 from l. Similarly, for the right node, B prefers r to l because r gives 4 as opposed to 2 from l. Because A can look ahead and anticipates B playing r regardless of her decision, she will prefer to play L (because she gets 2 instead of 1).
Underlying the completely different answers given by the simultaneous and sequential choices in a truel is a change in the rules of play. If play is sequential, the players do not have to fire simultaneously at the start, as assumed in a 3×3×3 strategic-form game. Rather, a player who moves first (A in our example)—and then the later players—would not fire, given that play continues until all bullets are expended or nobody chooses to fire.
In the extensive-form analysis, we ask of each player (it need not be A): Given your present situation (all alive), and the situation you anticipate will ensue if you fire first, should you do so? Because each player prefers living to the state he or she would induce by being the first to shoot (certain death), no one shoots.
This analysis suggests that truels might be more effective than duels, at least when played sequentially, in preventing the outbreak of conflict.
We will not try to develop this argument into a more general model. The main point is that a game tree allows for a look-ahead approach, whereby players compare the present state with possible future states—perhaps several steps ahead—to determine which moves to make. These choices, as we have seen, may lead to radically different outcomes compared with outcomes based on simultaneous choices.