21.3 21.2 Compound Interest and Geometric Growth
What you probably expected to happen to the savings account discussed in the last section is that during the second year, the account would earn interest of 10%, not on just the initial balance of $1000 (as with simple interest) but on the new balance of $1100. Then, at the end of the second year, 10% of $1100, or $110, would be added to the account.
Thus, during the second year, you would earn interest on both the principal of $1000 and on the $100 interest added. With this method, you receive more interest during the second year than during the first; that is, the account grows more during the second year. At the beginning of the third year, the account contains $1210, so at the end of the third year, you receive $121 in interest. Again, this is more than at the end of the preceding year.
Compound Interest DEFINITION
Compound interest is interest that is paid on both the original principal and accumulated interest.
Savings institutions usually compound interest and credit it to accounts more often than once a year-for example, quarterly (four times per year). With an interest rate of 10% per year and quarterly compounding, you get one-fourth of the rate, or 2.5%, paid in interest each quarter year. The “quarter” (three months) is the compounding period, or the time elapsing before interest is paid.
Compounding Period DEFINITION
The compounding period is the fundamental interval on which compounding is based, within which no compounding is done.
873
EXAMPLE 3 Interest Compounded Quarterly
Suppose again, as in Example 1, that you have $1000 deposited at 10% annual interest, but this time with interest compounded quarterly. How much is in the account at the end of one year?
At the end of the first quarter, you have the original balance plus $25 interest, so the balance at the beginning of the second quarter is $1025. During the second quarter, you receive interest equal to 2.5% of $1025, or $25.625, which is rounded up in posting to your account (since the fraction is half a cent or more) to $25.63. Continuing in this manner, the balance at the end of the first year is $1 103.82; see Table 21.1. (You should confirm all calculations in this chapter on your calculator.)
Even though the account was advertised as paying 10% interest, the interest for the year is $103.82, which is 10.382% of the original principal of $1000.
Self Check 3
How much would be in the account at the end of one year at 5% annual interest compounded semiannually (twice a year)?
- $1050.62
| Date | Beginning Balance |
Interest on Principal |
Interest on Interest |
Total Interest Added |
Ending Balance |
|---|---|---|---|---|---|
| January 1 | 1000.00 | ||||
| March 31 | 1000.00 | 25.00 | 0.00 | 25.00 | 1025.00 |
| June 30 | 1025.00 | 25.00 | 0.63 | 25.63 | 1050.63 |
| September 30 | 1050.63 | 25.00 | 1.27 | 26.27 | 1076.90 |
| December 31 | 1076.90 | 25.00 | 1.92 | 26.92 | 1103.82 |
Practical note: Without rounding the interest for each quarter, the interest for the year would have been not $1103.82 but $1103.81 (as shown in Table 21.2). Table 21.1 shows the results with rounding done only at the end of the year, while savings institutions must round at each posting and credit the rounded amount to your account. A spreadsheet program could duplicate the results of their computer programs; but in this table and in later calculations, we take the simpler route of rounding only at the final answer. Any differences will be very small; and if your answers differ by just a few cents, that will be OK.
If interest is compounded monthly (12 times per year) or daily (365 times per year), the resulting balance is even larger, as shown in Table 21.2. We will show you shortly the formula for these calculations. (The table also shows the results of continuous compounding, which we discuss later.)
| Years | Compounded Yearly |
Compounded Quarterly |
Compounded Monthly |
Compounded Daily |
Compounded Continuously |
|---|---|---|---|---|---|
| 1 | 1100.00 | 1103.81 | 1104.71 | 1105.16 | 1105.17 |
| 5 | 1610.51 | 1638.62 | 1645.31 | 1648.61 | 1648.72 |
| 10 | 2593.74 | 2685.06 | 2707.04 | 2717.91 | 2718.28 |
874
Interest Rates
Two accounts at the same annual rate of interest can produce different yields (amounts of interest), depending on how the compounding is done. To help prevent confusion for consumers, the Truth in Savings Act establishes terminology and calculation methods for interest.
A nominal rate is any stated rate of interest for a specified length of time, such as a 3% annual interest rate on a savings account or a 1.5% monthly rate on a credit-card balance. But by itself, a nominal rate does not indicate nor take into account whether or how often interest is compounded.
To keep interest rates straight, we use the following:
- for a nominal annual rate, which may or may not be compounded.
- for the rate during a compounding period, which can be a day, a month, or a year. There is no compounding done in a shorter interval than the compounding period. We call the periodic rate.
- for the number of compounding periods in a year.
We use only for an annual rate, and for a number of years. To avoid confusion, we don’t use the terminology annual percentage rate because that term has a special legal meaning just for loans (see Section 22.2, page 911).
Rate Per Compounding Period RULE
For a nominal annual rate compounded times per year, the rate per compounding period is
For that $1000 in savings at 10% compounded quarterly, we have and , so per quarter.
Geometric Growth
We look for the underlying mathematical pattern of compounding. We continue to use the values from our previous example-namely, an initial balance of $1000, an annual interest rate , quarterly compounding (so ), and hence quarterly interest rate . For quarterly compounding, you have at the end of the first quarter,
and at the end of the second quarter,
The pattern continues in this way, so that you have at the end of the fourth quarter. You use the calculator button marked to evaluate expressions such as ; on a spreadsheet, use the caret key (Shift-6), as in 1.025 4.
875
More generally, with initial principal and interest rate per compounding period, you have at the end of the first compounding period,
This amount can be viewed as a new starting balance. Hence, in the next compounding period, the amount grows to
The pattern continues, and we reach the following compound interest formula.
Compound Interest Formula RULE
An initial principal in an account that pays interest at a periodic interest rate per compounding period grows after compounding periods to
For convenience, we convert the general interest formula into one that is specific for years and annual rates. An annual rate of interest with compounding periods per year gives a rate per compounding period, and years contains compounding periods.
Compound Interest Formula for Several Years RULE
An initial principal in an account that pays interest at a nominal annual rate , compounded times per year, grows after years to
Notation for Savings DEFINITION
| amount accumulated, sometimes denoted FV for “future value” | |
| initial principal, sometimes denoted PV for “present value” | |
| nominal annual rate of interest | |
| number of years | |
| number of compounding periods per year | |
| total number of compounding periods | |
| periodic rate, the interest rate per compounding period |
The amount added each compounding period is proportional to the amount present at the time of compounding; we are adding to the amount . This type of growth is called geometric growth.
Geometric Growth (Exponential Growth) DEFINITION
Geometric growth (also called exponential growth) is growth proportional to the amount present.
876
EXAMPLE 4 Compound Interest for Several Years
Suppose that you have a principal of invested at 10% nominal interest per year. Using the compound interest formula , we determine the amount in the account after 10 years, for annual, quarterly, and monthly compounding.
Annual compounding. The annual rate of 10% gives , and after 10 years, the account has
Quarterly compounding. Then , and after 10 years () the account contains
Monthly compounding. Then . The amount in the account after 10 years () is
These entries are found in the last row of Table 21.2 on page 873.
Self Check 4
How much would be in the account after one year (not a leap year) with daily compounding?
- $1105.16
Algebra Review Appendix
Natural and Fractional Exponents
In doing the calculations, be sure to enter the interest rate as a decimal, and use as many decimal places as your calculator or spreadsheet carries (don’t round off until the final result). We show intermediate results with enough decimal places to give the final result to the nearest cent.
Simple Interest Versus Compound Interest
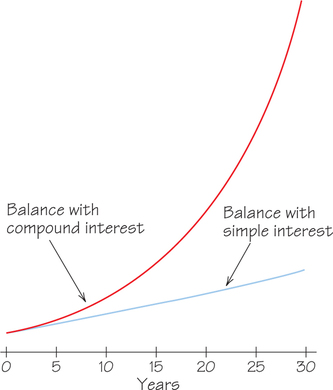
The amounts in accounts paying interest at 10% per year with compound and simple interest are shown in Table 21.3 and in the graph in Figure 21.1. They dramatically illustrate exponential growth at compound interest (the red curve above) compared with linear growth at simple interest (the blue straight line below).
| Years | Amount in Account with Compounded Interest |
Amount with Simple Interest |
|---|---|---|
| 1 | 1100.00 | 1100.00 |
| 2 | 1210.00 | 1200.00 |
| 3 | 1331.00 | 1300.00 |
| 4 | 1464.10 | 1400.00 |
| 5 | 1610.51 | 1500.00 |
| 10 | 2593.74 | 2000.00 |
| 20 | 6727.50 | 3000.00 |
| 50 | 117,390.85 | 6000.00 |
| 100 | 13,780,612.34 | 11,000.00 |
877
In some situations, the contrast between linear and exponential growth is not so immediately dramatic at first glance. In fact, for low rates of interest, or over a small number of years, the two are hard to distinguish. The much-overused phrase “growing exponentially” is often misused to mean “growing rapidly,” but in fact exponential growth need not be rapid.
The concepts of linear growth and exponential growth are realized in “populations” other than the dollars in banking, as we note below.
- Medical doctors: We noted earlier (page 872) that the population of U.S. medical doctors grows as if it were at simple interest (arithmetic growth) because the same number of doctors are added each year.
- Populations and food: On the other hand, general human populations tend to grow as if at compound interest (geometric growth), because the number of children born-the “interest"-increases as the population-the “balance"- increases. We examine models for population growth and for consumption of resources in Chapter 23. The distinction between arithmetic growth and geometric growth is fundamental to the major theory of demographer and economist Thomas Robert Malthus (1766–1834). He claimed that human populations grow geometrically but food supplies grow arithmetically, so that populations tend to outstrip their ability to feed themselves (see Spotlight 21.1).
- Global warming: The amount of carbon dioxide in the atmosphere, which contributes to global warming, has been growing since 1750 as a result of burning fuels. The amount is growing superexponentially-that is, faster than exponentially. The growth rate, or “interest rate,” itself increases every year. The current growth rate is about 0.57% per year. That seems like a very low rate of interest, but it is “interest” on what is already a large “principal” of carbon dioxide. The international Kyoto Protocol that went into effect in early 2005 (without U.S. participation) aims to lower worldwide emissions. Even if we limited emissions to a constant amount per year, the “principal” of carbon dioxide atoms in the atmosphere would still go up-and global warming would intensify-but just arithmetically, instead of superexponentially. We are in effect “saving” carbon dioxide into the atmosphere, at an unknown future cost.
878
- Nuclear waste: The situation of radioactive waste generated and stored at a nuclear power plant is more complicated. The absolute volume of waste added each year depends on the size and output of the power plant, not on the growing amount of waste in storage. Hence, the volume of waste grows arithmetically. What about the total amount of radioactive material in the storage dump? The radioactive ingredients decay very slowly into nonradioactive ones. While the radioactivity of waste already in storage is decreasing, new amounts of radioactive material are added each year. The situation requires a hybrid model that incorporates positive arithmetic growth (adding to the dump) accompanied by (much smaller) negative geometric growth (radioactive decay). The situation is like turning on the faucet in the bathtub while leaving the drain hole open a little. The faucet determines how fast water runs in, the height of the water determines how fast it runs out, and the two rates combined determine what happens to the volume of water in the tub.
Algebra Review Appendix
Graphs of Exponential Equations
Thomas Robert Malthus Spotlight 21.1
Thomas Robert Malthus (1766–1834), a 19th-century English demographer and economist, based a well- known prediction on his perception of the different patterns of growth of the human population and growth of the “population” of food supplies.
Although he believed that agricultural productivity would not be able to keep up with geometric growth in the human population, he concluded that over the long run, population growth could not remain geometric. It would be limited by war, disease, and starvation. This perspective was hardly an optimistic forecast and doubtless was responsible for a dreary image associated with his views.
Some observers suggest that the genocide in Rwanda in 1994 was indirectly a result of overpopulation compared with available food resources.
