8.6 8.5 Equally Likely Outcomes
An SRS gives all possible samples an equal chance to be chosen. Rolling two casino dice gives all 36 outcomes the same probability. When randomness is the product of human design, it is often the case that the outcomes in the sample space are all equally likely. In this case, Rules 1 and 2 force the assignment of probabilities.
Finding Probabilities of Equally Likely Outcomes PROCEDURE
If a random phenomenon has equally likely outcomes, then the probability of event A is
P(A)=count of outcomes in event Acount outcomes in sample space S
Furthermore, if another event B has a positive probability of occurring, then the probability of event A given B is
P(A|B)=count of outcomes in event A and Bcount of outcomes in event B
When outcomes are equally likely, we find probabilities by counting outcomes. The study of counting methods used to count those outcomes is called combinatorics.
Combinatorics DEFINITION
Combinatorics is the study of methods for counting.
One example of a counting method is the fundamental principle of counting (from Chapter 2, page 45): If there are a ways of choosing one thing, b ways of choosing a second after the first is chosen, …, and z ways of choosing the last item after the earlier choices, then the total number of choice sequences is a×b×⋯×z.

EXAMPLE 13 DNA Sequences
DNA Sequences
A strand of deoxyribonucleic acid (DNA) is a long sequence of the nucleotides adenine, cytosine, guanine, and thymine (abbreviated A, C, G, T). One helical turn of a DNA strand would contain a sequence of 10 of these acids, such as ACTGCCATGT. How many possible sequences of this length are there?
There are 4 letters that can occur in each position in the 10-letter sequence. Any of the 4 letters can be in the first position. Regardless of what is in the first position, any of the 4 letters can be in the second position, and so on. The order of the letters matters, so a sequence that begins AC will be different from one that begins CA. The number of different 10-letter sequences is more than 1 million:
4×4×4×4×4×4×4×4×4×4︸10 times=410=1,048,576
As big as that number is, consider that it would take a DNA sequence about 3 billion letters long to contain your entire genetic “blueprint”!
Knowing the number and frequency of DNA sequences has proven important in criminal justice. When skin or bodily fluids from a crime scene are “DNA fingerprinted,” the specific DNA sequences in the recovered material are extremely unlikely to be found in any suspect other than the perpetrator. The counting technique used in this example is expressed as Rule A on page 365.
EXAMPLE 14 Playing Songs
Playing Songs
Chapter 7, Example 4 (page 299), involved choosing a random sample of four different songs from a digital media player with a playlist of 27 different songs from Professor Lesser’s The Beatles One album. Now we ask: How many 4-song samples are possible from a collection of 27 songs? Like DNA sequences in Example 13, order matters here. (Performers and DJs know that the same four songs can feel quite different when the songs are played in a different order.) Unlike DNA sequences, listing the same item more than once is not allowed.

Any of the 27 songs can be chosen to be played first, but only the remaining 26 songs are available to be listed as the second song, so that there are 27×26 choices for the first two songs. Any of these choices leaves 25 songs for the third position and 24 for the fourth position. Surprisingly, the number of playlists of four different songs chosen from a list of 27 songs is almost half a million!
27×26×25×24=421,200
Now, suppose Professor Lesser’s favorite song is “Let it Be.” What is the probability that a randomly chosen playlist of four different songs will include this song? To answer the question, let event A be the playlists that include “Let it Be.” In order to apply the procedure for finding probabilities of equally likely outcomes, we need to count the number of outcomes in A. “Let it Be” could be the first, second, third, or fourth song on a playlist. If it is the first song, then 26×25×24=15,600 ways to complete the playlist by choosing three songs in order from the remaining 26 songs. The same is true if “Let it Be” is the second, third, or fourth song. Therefore, the number of outcomes in A is 4×15,600=62,400 and P(A)=62,400421,200≈0.148. Thus, “Let it Be” will be included roughly 15% of the time in randomly selected playlists of four different songs.
This scenario of choosing an ordered subset of k songs from a playlist of n songs is called a permutation.
Self Check 9
We continue with playlists from The Beatles One album.
- How many 5-song samples are possible from a collection of 27 songs?
- There are (27)(26)(25)(24)(23) = (421,200)(23) = 9, 687, 600 possible five-song playlists.
- Professor Lesser’s least favorite song from the album is “The Ballad of John and Yoko.” What is the probability that a randomly chosen playlist of five different songs will include this song?
Let A be the playlists that include “The Ballad of John and Yoko.” This song could be the first, second, third, fourth, or fifth song on a playlist. If it is the first song, then there are 26 × 25 × 24 × 23 = 358, 800 ways to complete the playlist by choosing four songs in order from the remaining 26 songs. The same is true if “The Ballad of John and Yoko” is the second, third, fourth, or fifth song. Therefore, the number of outcomes in A is 5 × 358, 800 = 1,794,000 and
P(A)=1,794,0009,687,600≈0.185
Permutation DEFINITION
A permutation is an ordered arrangement of k items that are chosen without replacement from a collection of n items. The number of arrangements can be notated as P(n, k), nPk′, or Pnk and has the formula
nPk=n×(n−1)×⋯×(n−k+1)
which is restated as Rule B in the rule box below.
Examples 13 and 14 both involve counting the number of arrangements of distinct items. They can each be viewed as specific applications of the fundamental principle of counting, and it is easier to think your way through the counting than to memorize a recipe. Nevertheless, because these two situations occur so often, they deserve to be given their own formal recognition as Rules A and B, respectively.
Counting Ordered Collections of Distinct Items RULE
Rule A. Suppose we have a collection of n distinct items. We want to arrange k of these items in order, and the same item can appear more than once in the arrangement. The number of possible arrangements is
n×n×⋯×n︸k times=nk
Rule B. (Permutations) Suppose we have a collection of n distinct items. We want to arrange k of these items in order, and any item can appear no more than once in the arrangement. The number of possible arrangements is
nPk=n×(n−1)×⋯×(n−k+1)
EXAMPLE 15 Four-Letter Words
Four-Letter Words
Suppose you have the following four Scrabble tiles: T, S, O, and P. How many four-letter sequences can you make using all four tiles? The only way to make a four-letter sequence is to use each letter exactly once. So, there are no repeats. This is a permutation by Rule B with n=4 and k=4. To think through the problem (rather than simply plugging into the formula), proceed like this: Any of the four letters can be chosen first, any of the three that remain can be chosen second, and so on. The number of permutations, therefore, is
4×3×2×1=24

This example shows us that the permutation of all n elements of a collection yields the product of the first n integers. This expression of factors is special enough to have its own name: factorial (discussed in Chapter 2, and again in Chapter 11).
Now, let’s get back to the Scrabble game. It turns out that only 6 of the 24 possible sequences of 4 letters are actually words in the English language (can you figure out all 6 words?), so the probability that a permutation (chosen at random from these 4 tiles) I will be an actual word is 624=14.
Factorial DEFINITION
The factorial for a positive integer n equals the product of the first n positive integers. The notation for “n factorial” is n!:
n!=n×(n−1)×(n−2)×⋯×3×2×1
By convention, we define 0! to equal 1, which can be interpreted as saying there is one way to arrange zero items.
Self Check 10
Determine the value of 6!
- 6!=6×5×4×3×2×1=720
Factorial notation lets us write a long string of multiplied factors very compactly. Using factorial notation, the expression for permutations in Rule B can now be rewritten as follows:
nPk=n!(n−k)!
Permutations and factorials can be tedious to compute for large values of n, but even a scientific calculator should have a key labeled n! or x! If you have only a basic calculator without a factorial key, the expression n×(n−1)×⋯×(n−k+1) will involve fewer multiplications than evaluating n!(n−k)!, by first calculating n! and (n−k)!, because it has already incorporated all the cancellations between numerator and denominator—namely, cancelling the positive integers from 1 to n−k.
EXAMPLE 16 Computing a Permutation: Factorial Formula or Rule B?
Computing a Permutation: Factorial Formula or Rule B?
Suppose a club has 10 members. How many slates of president, vice president, and treasurer are possible? This is a permutation. We must select three club members and arrange them in the three elective offices. In other words, we need to compute 10P3. We’ll do this in two ways. First, we’ll use the formula above and the factorial key on a calculator. Next, we’ll expand the formula, cancel, and arrive at the calculation shown for Rule B. You can decide which is easier.
10P3=10!(10−3)!=10!7!=3,628,8005,040Calculation using calculator's factorial key 10P3=10!(10−3)!=10!7!=(10)(9)(8)(7!)7!Calculation done by hand
In Example 16, counting the number of slates for club officers is a permutation because the arrangement of people in the elected offices matters. Being listed as president is different from being listed as treasurer. However, what if the club planned to send a delegation of three of its members to a conference? In this situation, {Joe, Mia, Mizan} is the same delegation as {Mizan, Mia, Joe}. The arrangement of the names doesn’t change who is representing the club at the conference. How many different delegations can be selected? This is an example of a combination. The 720 ways to select the three-person slate of officers from Example 16 overshoots the number of ways to select a delegation because it counts each of the 3! ways to list three different club members chosen as distinct. So the number of ways to choose the three-member delegation is 7203!=120.
Combination DEFINITION
A combination is an unordered selection of k items that are chosen without replacement from a collection of n items. The number of combinations can be notated as (nk), C(n, k), or nCk, which is often pronounced “n choose k”:
nCk= nPkk!=n×(n−1)×⋯×(n−k+1)k!=n!k!(n−k!)
which is Rule D in the next rule box.
EXAMPLE 17 Winning the Texas Lottery?
Winning the Texas Lottery?
Most states have lottery games. The Texas Lottery (www.txlottery.org) has a Lotto Texas game that involves choosing six numbers from the set of whole numbers from 1 to 54. You win (at least a share of) the jackpot so long as the collection of numbers you pick is the same collection that the lottery selects. Repetition is not allowed—that is, the same number can’t be picked twice in the same drawing. Unlike permutations, order does not matter here. A person who chooses {49, 12, 18, 26, 22, 5} will receive the same payout as a person who chooses {26, 18, 12, 49, 5, 22}.
This is a perfect setup for a combination because the order of the selected numbers doesn’t matter. The number of collections of lottery balls is “54 choose 6,” or
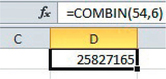
54C6= 54P66!=54×53×52×51×50×496×5×4×3×2×1=25,827,165
possible sets of numbers. Because only one of these sets of numbers will correspond to the jackpot, the probability of your ticket winning (at least a share of) the jackpot is 125,827,165.
More generally, the scenario of choosing an unordered subset of k balls from a collection of n different balls is a combination.
If it’s hard to remember the difference between combinations (Rule D) and permutations (Rule B), use this memory aid: “Permutations presume positions; combinations concern collections.” For completeness, we also provide a formula (Rule C) for unordered collections in which repetition is allowed, but an explanation is beyond the scope of this chapter and we will not use it again.
Counting Unordered Collections of Distinct Items RULE
Rule C. Suppose that we have a collection of n distinct items. We want to select k of those items with no regard to order, and any item can appear more than once in the collection. The number of possible collections is
(n+k−1)!k!(n−1)!
Rule D. (Combinations) Suppose we have a collection of n distinct items. We want to select k of these items with no regard to order, and any item can appear no more than once in the collection. The number of possible selections is
nCk=n!k!(n−k)!
Rules A, B, C, and D can be summarized in Table 8.7.
| Repetition is allowed | Repetition is not allowed | |
|---|---|---|
| Order does matter | Rule A: n×n×⋯×n=nk n is multiplied by itself k times | Rule B (permutation):n!(n−k)!=n×(n−1)×⋯×(n−k+1) |
| Order does not matter | Rule C: (n+k−1)!k(n−1)! | Rule D (combination):n!k!(n−k)! |
Self Check 11
In each of the following situations, decide whether the permutation rule or combination rule should be used to determine the number of different ways the positions can be filled by the job applicants. Show the results for each situation.
- A university library posts an ad for three library technicians. There are 15 applicants.
- Combination: 15C3=15!3!(15−3)!=(15)(14)(13)(3)(2)=455
- A hospital posts an ad for three nursing positions: a day nursing supervisor, a night nursing supervisor, and a nursing coordinator. There are 15 applicants.
- Permutation: 15P3=15!(15−3)!=(15)(14)(13)=2730
Although it is important to have some experience computing permutations, factorials, and combinations by hand, it can be time consuming. Spotlight 8.3 shows how technology can be used to speed up the process.
Using Technology to Compute Permutations, Factorials, and Combinations 8.3
8.3
Graphing calculators and spreadsheets have built-in functions to compute permutations, factorials, and combinations. Below are instructions for TI-84 graphing calculators and Excel. (Not using a TI-84 calculator or Excel? Find the instructions for your particular calculator or spreadsheet on the Internet.)
TI-84 Graphing Calculators Permutation
To calculate nPr:
- Enter the value for n.
- Press MATH→PRB and select 2 (for npr).
- Enter the value for r and then press ENTER.
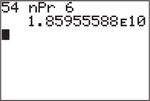
We illustrate with the example 54P6:
Press 5 4 MATH→PRB, and then press 2 6 ENTER. Here are the results.

Scientific Notation
Because the answer—18,595,558,800—is so large, the calculator used its version of scientific notation to report it.
Factorial
To calculate n!:
- Enter the value for n.
- Press MATH→PRB , select 4 (for !), and then press ENTER.
We illustrate with the example 6!:
Press 6 MATH→PRB and then press 4 ENTER. The answer should be 720 (as you should have discovered in Self Check 10.)
Combination
To calculate nCr:
- Enter the value for n.
- Press MATH→PRB and select 3 (for nCr).
- Enter the value for r and then press ENTER.
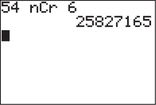
We illustrate with the example 54C6:
Press 5 4 MATH→PRB and then press 3 6 ENTER. Here are the results.
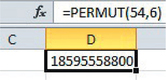
Excel Permutation
To calculate nPk:
- Click on an empty cell.
- Key in the formula =PERMUT (the value for n, the value for k) and then press Enter
We illustrate with the example 54P6:
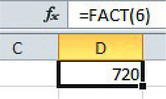
Factorial
To calculate n!:
- Click on an empty cell.
- Key in the formula =FACT (the value for n) and then press Enter.
We illustrate with the example 6!:
Combination
To calculate nCk:
- Click on an empty cell.
- Key in the formula =COMBIN (the value for n, the value for k) and then press Enter.
We illustrate with the example 54C6:
Self Check 12
Use a calculator or spreadsheet program with built-in functions for calculating permutations, factorials, and combinations to determine the following: 30P7, 7!, 30C7.
- 30P7=10,260,432,000; 7!=5,040; 30C7=2,035,800
The topic of Spotlight 8.4 is determining the likelihood that a group of people share the same birthday. In determining this likelihood, we assume a discrete uniform probability model in which all days of the year are assumed to be equally likely to be a birthday. (While this assumption is not perfectly satisfied, it turns out that any deviations from it only make the probability of a match even higher.) If we consider the continuous uniform probability model (see Chapter 5, Exercise 73 on page 238) of the day and time someone is born, then more advanced mathematics shows that only 17 people are required for there to be at least a 50% chance that at least two birth times are within 24 hours of each other! In the next two sections, we will examine continuous and discrete probability models in more detail.
Birthday Coincidences 8.4
8.4
If we ignore leap day (February 29), there are 365 possible birthdays a person can have. So if 366 people are gathered, there’s a 100% chance that at least two people share the same birthday. Now, if only 23 people are gathered, what do you think is the probability of any birthday matches? Guess before reading further.
Now imagine these 23 people enter a room one at a time, adding their birthday to a list in the order they enter. Using n=365 and k=23, Rule A gives us the total number of lists of 23 birthdays: 36523. Rule B gives us how many of those lists have birthdays that are all different: 365P23. Using the rule for equally likely outcomes (assuming each day of the year is equally likely to be a randomly chosen person’s birthday), we conclude that the probability of all birthdays being different is the result from Rule B divided by the result from Rule A:
365P2336523=365×364×⋯×34336523
Alternatively, we could assume independence of birthdays and use Probability Rule 6 (multiplication rule for independent events). The second person who walks in has a 364/365 chance of not matching person #1. The third person who walks in has a 363/365 chance of not matching persons #1 or #2, and so on. Verify that you get the same product by multiplying this string of fractions:
364365×363365×⋯×343365

Either way, our final step to find the probability of getting at least one match is to subtract that answer from 1 (using Rule 3, the complement rule), and we obtain the surprisingly high value of 51%!
A rough way to make the result seem plausible (devised by Manfred Borovcnik, a researcher in probability and statistics education) is to say that with 23 people, you would expect to have about two people born in each month. In one month, the chance that one person matches someone else’s birthday is about 1/30. Expecting “1/30 of a match” per month adds up to 12/30 of a match for the year, and 12/30 is not much less than 50%.
Because we underestimate the number of potential opportunities for “coincidences,” we are surprised that they happen as often as they do. But as statistician Jessica Utts notes, if something has a one in a million chance of happening to any person on a given day, this rare event will happen to roughly 300 people in the United States each day!