2.1 Business Efficiency 2

- 2.1 Hamiltonian Circuits
- 2.2 Traveling Salesman Problem
- 2.3 Helping Traveling Salesmen
- 2.4 Minimum-Cost Spanning Trees
- 2.5 Critical-Path Analysis
In the preceding chapter, we saw that there was an easy way of telling whether a connected graph has a circuit that traverses each of the edges of a graph exactly once—for example, a route for a snowplow that covers the streets of a section of a town. However, the situation changes drastically if we make a seemingly small change in the problem: When is it possible to find a route along distinct edges of a graph that visits each vertex once and only once in a simple circuit? Perhaps there has been a hurricane and it is important to check whether the storm sewers at every corner in town are clogged. We want all the sewers to be checked. However, doing so typically will not require that all the streets in the town be traversed.
This problem is called the Hamiltonian circuit problem, and, like the Euler circuit problem, it is a graph theory problem. The Hamiltonian circuit problem has many applications—for example, the delivery of parcels, traffic light inspections, or gas meter readings. Suppose inspections or deliveries need to be made at each vertex (rather than along each edge) of a graph. An “efficient” tour of the graph would be a route that started and ended at the same vertex and passed through all the vertices without reuse, or repetition; that is, the route would be a Hamiltonian circuit. Such routes would be useful for inspecting for blocked sewers, for delivering mail to drop-off boxes, which hold heavy loads of mail so that urban postal carriers do not have to carry them long distances, or for delivering meals to needy elderly people.
Hamiltonian Circuit DEFINITION
A tour that starts at a vertex of a graph and visits each vertex once and only once, returning to where it started, is called a Hamiltonian circuit.
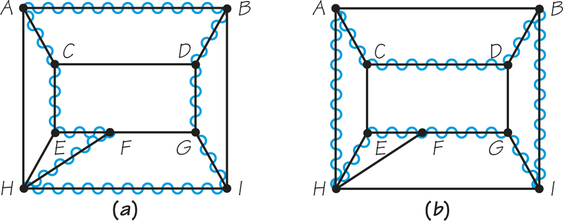
For example, the wiggly line in Figure 2.1a shows a circuit we can take to tour that graph, visiting each vertex once and only once. This tour can be written ABDGIHFECA. Note that another way of writing the same circuit would be ACEFHIGDBA or EFHIGDBACE A different circuit visiting each vertex once and only once would be CDBIGFEHAC (Figure 2.1b). Do not be confused because C is written twice when we write down this list of vertices. We can think of the circuit as starting at any of its vertices, but we do start and end at the same vertex.