Problems
(Solutions to problems marked * appear at the back of this book. Problems adapted to use calculus are available online at www.macmillanhighered.com/
In 1969, television companies were the largest single product advertisers on television. That same year, the Surgeon General of the United States released a report linking smoking to adverse health consequences. Shortly thereafter, the federal government banned cigarette companies from advertising on television. Suppose you were an executive at a tobacco company at that time. Read Section 11.1 carefully, then explain how you might react to the federal government’s advertising ban, and why.
Suppose you and a rival are the only producers of oysters in an isolated town. Every morning you both dive for oysters that you will sell in the market that afternoon. Each morning, you both have a choice of bringing up 10 or 20 dozen oysters; each dozen you bring up has a marginal cost of $10. If 20 dozen oysters are brought to market in total, they will sell for $35 each. If 30 dozen oysters are brought to market, they will sell for $25 each. If 40 dozen oysters are brought to market, they will sell for $20 each. The following table shows the profit you and a rival can expect to earn based on your choice of bringing up 10 or 20 dozen oysters each:
Your Rival 10 dozen 20 dozen You 10 dozen 250 , 250 150 , 300 20 dozen 300 , 150 200 , 200 Verify that the profits represented in the table above are accurate.
Where is the Nash equilibrium in the game you and your rival play?
Is the Nash equilibrium one that you and your rival would agree to if you were to discuss production before diving each day? If not, explain why that agreement is unlikely to be honored.
Draw a parallel between the game described in this problem and the advertising game Disney and Warner Brothers played in Table 11.1
Because cooking soufflés is incredibly difficult, the supply of soufflés in a small French town is controlled by two bakers, Gaston and Pierre. The demand for soufflés is given by P = 30 – 2Q, and the marginal and average total cost of producing soufflés is $6. Because baking a soufflé requires a great deal of work and preparation, each morning Gaston and Pierre make a binding decision about how many soufflés to bake.
Suppose that Pierre and Gaston agree to collude, evenly splitting the output a monopolist would make and charging the monopoly price.
Derive the equation for the monopolist’s marginal revenue curve.
The marginal revenue is MR = 30 – 4Q.
Determine the profit-
maximizing collective output for the cartel. The profit-
maximizing collective output for the cartel solves the condition MR = MC; that is, 30 – 4Q = 6
4Q = 24
Q = 6
Determine the price Pierre and Gaston will be able to charge.
Gaston’s profit is now
(P – ATC) × Q = ($16 – $6) × 3 = $30
Hence, Gaston lost $6.
Determine profits for Pierre and Gaston individually, as well as for the cartel as a whole.
Pierre and Gaston split the output equally; hence, each of them gets
(P – ATC) × Q = ($18 – $6) × 3 = $36
The profit for the cartel is $72.
Suppose that Pierre cheats on the cartel agreement by baking one extra soufflé each morning.
What does the extra production do to the price of soufflés in the marketplace?
The extra production of soufflés decreases the price in the marketplace; that is,
P = 30 – 2Q = 30 – (2 × 7) = $16
Calculate Pierre’s profit. How much did he gain by cheating?
Pierre’s profit is now
(P – ATC) × Q = ($16 – $6) × 4 = $40
Hence, Pierre gained $4 by cheating.
Calculate Gaston’s profit. How much did Pierre’s cheating cost him?
Gaston’s profit is now
(P – ATC) × Q = ($16 – $6) × 3 = $30
Hence, Gaston lost $6.
How much potential profit does the group lose as a result of Pierre’s cheating?
The profits are now $40 + $30 = $70. Therefore, as a result of Pierre’s cheating, the group loses $2 of potential profit.
Suppose that Gaston, fed up with Pierre’s behavior, also begins baking one extra soufflé each morning.
How does the extra production affect the price of soufflés in the marketplace?
460
The extra production of soufflés decreases the price further in the marketplace; that is,
P = 30 – 2Q = 30 – 2(8) = $14
Calculate Gaston’s profit. How much did he gain by cheating?
Gaston’s profit is now
(P – ATC) × Q = ($14 – $6) × 4 = $32
Hence, Gaston gains $2 compared to the previous scenario.
Calculate Pierre’s profit. How much did Gaston’s cheating cost him?
Pierre’s profit is now
(P – ATC) × Q = ($14 – $6)4 = $32
Hence, Pierre loses $8 compared to the previous scenario.
How much potential profit does the group lose as a result of Pierre’s and Gaston’s cheating?
The group’s profits are $32 + $32 = $64. Therefore, they lose in total $8 of potential profit.
Demonstrate that it is in neither Pierre’s nor Gaston’s best interest to cheat further on their agreement.
If they decide to continue cheating, the price of soufflés will decrease, which will result in a reduction of profit for both individuals. More specifically, if one cheats further, the total output rises to 9. The price becomes
P = 30 – 2Q = 30 – 2(9) = $12
The profit for the cheater is now
(P – ATC) × Q = ($12 – $6) × 5 = $30
SB-
19 Hence, neither Pierre nor Gaston has an incentive to cheat as the cheater’s profit falls from $32 to $30.
Suppose in the previous problem that Gaston can produce soufflés at a constant marginal cost of $5, but Pierre produces soufflés for $7. Together, they collude to produce 3 units each.
How much profit will each producer earn? What will be the total profit of the cartel?
Gaston observes that he is a more efficient producer than Pierre, and suggests that if they are going to produce 6 units, the cartel’s interests are better served if Gaston produces all of the soufflés.
If Gaston produces and sells all of the soufflés and Pierre produces nothing, what happens to the profit of the cartel?
Is Pierre likely to agree not to produce any soufflés?
Suppose Gaston offers to pay Pierre not to produce any soufflés. How much would Gaston potentially be willing to offer? What is the minimum offer that Pierre should accept?
Suppose that the deal in part (iii) is reached for Pierre’s minimum price. What happens to Pierre’s profit if he cheats on his agreement with Gaston and increases his output from zero soufflés to one? What happens to Gaston’s profit?
Compare Pierre’s incentive to cheat under this arrangement with the incentive that exists when they split production equally. Also compare Gaston’s vulnerability to Pierre’s cheating under both arrangements. Why might this cartel choose to use the less profitable method of each member producing 3 units to the potentially more profitable method of having Gaston produce everything?
The Organization of Petroleum Exporting Countries (OPEC) is a cartel that attempts to keep oil prices high by restricting output. As part of that process, each member nation is assigned a production quota; most members have nationalized their oil industry so that the government controls overall production. However, member nations routinely exceed their production targets. Read “What Makes Collusion Easier” in Section 11.2; then explain why OPEC often has difficulty keeping output low and prices high. Do you think that violators are more likely to emerge from politically stable countries, or unstable countries? From monarchies or democracies?
Suppose that the inverse market demand for pumpkins is given by P = $10 – 0.05Q. Pumpkins can be grown by anybody at a constant marginal cost of $1.
If there are lots of pumpkin growers in town so that the pumpkin industry is competitive, how many pumpkins will be sold, and what price will they sell for?
Suppose that a freak weather event wipes out the pumpkins of all but two producers, Linus and Lucy. Both Linus and Lucy have produced bumper crops, and have more than enough pumpkins available to satisfy the demand at even a zero price. If Linus and Lucy collude to generate monopoly profits, how many pumpkins will they sell, and what price will they sell for?
Suppose that the predominant form of competition in the pumpkin industry is price competition. In other words, suppose that Linus and Lucy are Bertrand competitors. What will be the final price of pumpkins in this market — in other words, what is the Bertrand equilibrium price?
At the Bertrand equilibrium price, what will be the final quantity of pumpkins sold by both Linus and Lucy individually, and for the industry as a whole? How profitable will Linus and Lucy be?
Would the results you found in parts (c) and (d) be likely to hold if Linus let it be known that his pumpkins were the most orange in town, and Lucy let it be known that hers were the tastiest? Explain.
Would the results you found in parts (c) and (d) hold if Linus could grow pumpkins at a marginal cost of $0.95?
Suppose that three grocery stores sell Bubba’s Gourmet Red Beans and Rice. Bullseye market is able to acquire, stock, and market them for $2.00 per package. OKMart can acquire, stock, and market them for $1.98 per package. SamsMart can acquire, stock, and market them for $1.96 per package.
If the three competitors are located in close proximity to one another, so that the cost of going to a different store to purchase red beans and rice is negligible, and if the market for prepackaged gourmet red beans and rice is characterized by Bertrand competition, what will the prevailing market price be?
461
Where will customers buy their red beans and rice? Bullseye, OKMart, or SamsMart? What does your answer suggest about the potential rewards to small improvements in efficiency via cost-
cutting? Suppose that each day, equal numbers of customers begin their shopping at each of the three stores. If the cost of going to a different store to purchase red beans and rice is 3 cents, is the Bertrand result likely to hold in this case? Where will customers purchase red beans and rice? Where will they not purchase them?
Jack and Annie are the only sellers of otters in a three-
state area. The inverse market demand for otters is given by P = 100 – 0.5Q, where Q = the total quantity offered for sale in the marketplace. Specifically, Q = qJ + qA, where qJ is the amount of otters offered for sale by Jack and qA is the amount offered for sale by Annie. Both Jack and Annie can produce otters at a constant marginal and average total cost of $20. Graph the market demand curve. What would be the prevailing price and quantity if this industry were controlled by a monopolist?
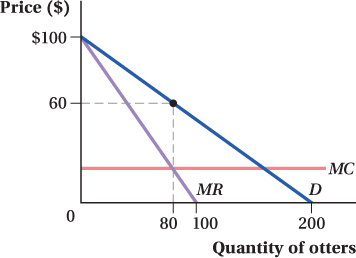
The profit-
maximizing quantity for a monopolist is MR = 100 – Q = 20 = MC
Q = 80
Thus, the price is
P = 100 – 0.5Q = 100 – 0.5 × 80 = $60
Suppose that Jack solves part (a) and announces that he will bring half of the monopoly quantity to market each day.
The market inverse demand for otters is given by P = 100 – 0.5(qJ + qA ). Plug in Jack’s announced output for qA to solve for the residual demand curve faced by Annie.
Solve for, and graph, the residual marginal revenue curve faced by Annie.
Given Annie’s otter production cost of $20, how many units should Annie bring to market to maximize her profit?
Find Annie’s residual demand by using Jack’s quantity in the market inverse demand:
P = 100 – 0.5(qJ + qA) = 100 – 0.5(40 + qA)
= 80 – 0.5 qA
The residual marginal revenue for Annie is MR = 80 – qA.
In order to maximize profit, Annie will set MR = MC:
80 – qA = 20
qA = 60
Annie’s profit-
maximizing quantity is 60. Given your answers to (b), what will the industry quantity and final price of otters be? How much profit will Annie earn? Jack?
The quantity produced by both of them is 100. Therefore, the final price of otters is
P = 100 – 0.5Q = 100 – 0.5 × 100 = $50
Annie’s profit is
(P – ATC) × Q = ($50 – $20) × 60 = $1,800
Jack’s profit is
(P – ATC) × Q = ($50 – $20) × 40 = $1,200
Suppose that Jack observes Annie’s output from part (b). Find Jack’s residual demand and marginal revenue curves, and determine if Jack should adjust his output in response to Annie’s choice of qA. What will the new price of otters be?
The residual demand curve for Jack is
P = 100 – 0.5(qJ + qA) = 100 – 0.5(qJ + 60)
= 70 – 0.5 qJ
The residual marginal revenue for Jack is
MRJ = 70 – qJ
In order to maximize the profit, Jack should produce the quantity where MC = MR:
70 – qJ = 20
qJ = 50
So, instead of producing 40 as he announced, Jack should choose a quantity of 50. Together, he and Annie will supply a quantity of 110. The market price can be found using Q = 110 in the inverse demand:
P = 100 – 0.5Q = 100 – 0.5(110) = $45
Annie’s profit is (P – ATC) × qA = ($45 – $20)
× 60 = $1,500.
Jack’s profit is (P – ATC) × qJ = ($45 – $20)
× 50 = $1,250.
Is the outcome you found in part (d) an equilibrium outcome? How do you know?
Solving for the Cournot equilibrium, we get
P = 100 – 0.5(qJ + qA)
The marginal revenue for Jack is
MRJ = 100 – qJ – 0.5qA
In equilibrium, MC = MR. Hence,
MRJ = 100 – qJ – 0.5qA = 20 = MC
qJ = 80 – 0.5qA
Similarly, for Annie
MRA = 100 – 0.5qJ – qA
and
qA = 80 – 0.5qJ
Thus,
qJ = 80 – 0.5(80 – 0.5qJ)
= 53.33
Likewise,
qA = 53.33
Therefore, in equilibrium the price is
P = 100 – 0.5(qJ + qA) = $46.66
Therefore, the outcome found in part (d) is not an equilibrium outcome.
-
The platypus is a shy and secretive animal that does not breed well in captivity. But two breeders, Sydney and Adelaide, have discovered the secret to platypus fertility and have effectively cornered the market. Zoos across the globe come to them to purchase their output; the world inverse demand for baby platypuses is given by P = 1,000 – 2Q, where Q is the combined output of Sydney (qS ) and Adelaide (qA ).
Sydney wishes to produce the profit-
maximizing quantity of baby platypus. Given Adelaide’s choice of output, qA, write an equation for the residual demand faced by Sydney. The inverse demand is
P = 1,000 – 2(qS + qA)
The residual demand faced by Sydney is
P = (1,000 – 2qA) – 2qS
Derive Sydney’s residual marginal revenue curve.
The residual marginal revenue is
MRS = (1,000 – 2qA) – 4qS
Assume that the marginal and average total cost of raising a baby platypus to an age at which it can be sold is $200. Derive Sydney’s reaction function.
MRS = 1,000 – 2qA – 4qS = 200 = MC
qS = 200 – 0.5qA
Repeat steps (a), (b), and (c) to find Adelaide’s reaction function to Sydney’s output choice.
The residual marginal revenue for Adelaide is
MRA = 1,000 – 4qA – 2qS
Thus,
MRA = 1,000 – 4qA – 2qS = 200 = MC
qA = 200 – 0.5qS
Substitute Sydney’s reaction function into Adelaide’s to solve for Adelaide’s profit-
maximizing level of output. Then use your answer to find Sydney’s profit- maximizing level of output. Adelaide’s reaction function as a function of Sydney’s quantity is
qA = 200 – 0.5 qS = 200 – 0.5(200 – 0.5 qA)
0.75qA = 100
qA = 133.33
Because both firms have a constant marginal cost of $200, the profit-
maximizing level of output for Sydney is also 133.33. Determine industry output, the price of platypus, and the profits of both Sydney and Adelaide.
The output of the industry is 266.66. Thus, the price is
P = 1,000 – 2(qS + qA) = 1,000 – 2(266.66)
= $466.66
Both Sydney and Adelaide earn the same profit, which is equal to
(P – ATC) × Q = ($466.66 – $200) × 133.33
≈ $35,556
Total industry profit is equal to $71,111.11.
If Adelaide were hit by a bus on her way home from work, and Sydney were to become a monopolist, what would happen to industry quantity, price, and profit?
If Sydney becomes a monopolist, she would set the price so that the marginal cost equals the marginal revenue, that is,
MR = 1,000 – 4Q = 200 = MC
Q = 200
The price is
P = 1,000 – 2Q = 1,000 – 2 × 200 = $600
The profit is now
(P – ATC) × Q = ($600 – $200) × 200 = $80,000
Therefore, the quantity sold decreases, price increases, and so does the profit for the industry as a whole.
-
Suppose that two firms are Cournot competitors. Industry demand is given by P = 200 – q1 – q2, where q1 is the output of Firm 1 and q2 is the output of Firm 2. Both Firm 1 and Firm 2 face constant marginal and average total costs of $20.
Solve for the Cournot price, quantity, and firm profits.
Firm 1 is considering investing in costly technology that will enable it to reduce its costs to $15 per unit. How much should Firm 1 be willing to pay if such an investment can guarantee that Firm 2 will not be able to acquire it?
How does your answer to (b) change if Firm 1 knows the technology is available to Firm 2?
Consider the demand for boccie balls shown in the diagram below. Demand is given by P = 80 – Q. Boccie balls can be produced at a constant marginal and average total cost of $20.
462

If the boccie ball industry were perfectly competitive, what quantity would be sold, and what price would prevail in the market?
Suppose that the boccie ball industry were a monopoly. Draw in a marginal revenue curve and determine the profit-
maximizing quantity. Divide the monopoly (one-
firm) quantity by the competitive quantity to determine the proportion of competitive output that a monopolist provides. Present your answer in reduced fractional form. Determine the price, and draw a dot on the demand curve indicating the monopolist’s price and quantity.
Suppose the boccie ball industry were a Cournot duopoly (two-
firm), with two firms. Use the procedures developed in this chapter to determine the industry output. Divide the duopoly quantity by the competitive quantity to determine the proportion of competitive output that a duopoly provides. Present your answer in reduced fractional form.
Determine the price, and draw a dot on the demand curve indicating the duopoly’s price and quantity.
Hypothesize as to the fraction of competitive output that would be sold if the boccie ball industry had three identical Cournot competitors. Then check your answer by deriving reaction functions for a three-
firm oligopoly and solving for each firm’s output. In general, what fraction of the competitive output level will be brought to market if there are N identical firms in the industry?
What happens to the quantity sold as more competitors are added to the industry? The price? What happens to consumer surplus and deadweight loss? Does this provide support for the government’s desire to ensure competitive industries rather than monopolies or small oligopolies?
-
Two organic emu ranchers, Bill and Ted, serve a small metropolitan market. Bill and Ted are Cournot competitors, making a conscious decision each year regarding how many emus to breed. The price they can charge depends on how many emus they collectively raise, and demand in this market is given by Q = 150 – P. Bill raises emus at a constant marginal and average total cost of $10; Ted raises emus at a constant marginal and average total cost of $20.
Find the Cournot equilibrium price, quantity, profits, and consumer surplus.
Suppose that Bill and Ted merge, and become a monopoly provider of emus. Further, suppose that Ted adopts Bill’s production techniques. Find the monopoly price, quantity, profits, and consumer surplus.
Suppose that instead of merging, Bill considers buying Ted’s operation for cash. How much should Bill be willing to offer Ted to purchase his emu ranch? (Assume that the combined firms are only going to operate for one period.)
Has the combination of the two ranches discussed above been good for society or bad for society? Discuss how the forces of monopoly power and increased efficiency tend to push social well-
being in opposite directions.
The market for nutmeg is controlled by two small island economies, Penang and Grenada. The market demand for bottled nutmeg is given by P = 100 – qP – qG, where qP is the quantity Penang produces and qG is the quantity Grenada produces. Both Grenada and Penang produce nutmeg at a constant marginal and average cost of $20 per bottle.
Verify that the reaction function for Grenada is given by qG = 40 – 0.5qP. Then verify that the reaction function for Penang is given by qP = 40 – 0.5qG.
The reaction function for Grenada is
MRG = 100 – qP – 2qG = 20 = MC
qG = 40 = 0.5qP
The reaction function for Penang is
MRP = 100 – 2qP – qG = 20 = MC
qP = 40 – 0.5qG
Find the Cournot equilibrium quantity for each island. Then solve for the market price of nutmeg and for each firm’s profit.
The equilibrium quantity for Grenada is
qG = 40 – 0.5qP = 40 – 0.5(40 – 0.5qG)
= 20 + 0.25qG
= 26.67
The equilibrium quantity for Penang is
qP = 40 – 0.5qG = 40 – (0.5 × 26.67) = 26.67
The market price is then
P = 100 – qP – qG = $46.67
The profit for Grenada is
(PG – ATCG) × QG = ($46.67 – $20)
× 26.67 = $711.11
The profit for Penang is
(PP – ATCP) × QP = ($46.67 – $20)
× 26.67 = $711.11
Suppose that Grenada transforms the nature of competition to Stackelberg competition by announcing its production targets publicly in an attempt to seize a first-
mover advantage. Grenada must first decide how much to produce, and to do this, it needs to know the demand conditions it faces. Substitute Penang’s reaction function into the market demand curve to find the demand faced by Grenada.
The demand faced by Grenada is
P = 100 – qP – qG = 100 – (40 – 0.5qG) – qG
= 60 – 0.5qG
Based on your answer to the problem above, find the marginal revenue curve faced by Grenada.
463
The marginal revenue for Grenada is
MRG = 60 – qG
Equate marginal revenue with marginal cost to find Grenada’s output.
Grenada’s output is
MRG = 60 – qG = 20 = MC
qG = 40
Plug Grenada’s output into Penang’s reaction function to determine Penang’s output.
Penang’s output is
qP = 40 – 0.5qG = 40 – (0.5 × 40) = 20
Plug the combined output of Grenada and Penang into the market demand curve to determine the price. How do the industry quantity and price compare to those under Cournot competition?
The price is
P = 100 – qP – qG = 100 – 20 – 40 = $40
SB-
21 The industry quantity is greater compared to the Cournot competition, and the price is lower.
Determine profits in Grenada and Penang. How do the profits of each compare to profits under Cournot competition? Is there an advantage to being the first-
mover? The profit for Grenada is
(PG – ATCG) × QG = ($40 – $20) × 40
= $800
The profit for Penang is
(PP – ATCP) × QP = ($40 – $20) × 20
= $400
Grenada’s profit is greater in the Stackelberg competition, whereas the profit for Penang is smaller in the Stackelberg competition. Therefore, the first-
mover is better off.
Consider the Cournot–
Stackelberg competing islands of Penang and Grenada discussed in the previous problem. What will happen to Grenada’s and Penang’s output if: Grenada’s cost of production decreases to $16, while Penang’s stays at $20. Explain.
Penang’s cost of production decreases to $16, while Grenada’s stays at $20. Explain.
August and Francois are the only sellers of sparkling water at a market in a small, rural French town. They obtain their sparkling water for free from wells in their backyards and transport it to the market in wheelbarrows; neither has access to motorized transportation. Identify the type of oligopoly (Cournot, Bertrand, Stackelberg) that is the best fit for each situation below, and explain your reasoning:
August and Francois both live four hours’ walk from the market.
August and Francois both live half a block from the market.
August lives a long walk away, but is an early riser who always arrives at 8:00 A.M.; Francois lives quite close and never shows until 8:30.
Internet users in a small Colorado town can access the Web in two ways: via their television cable or via a digital subscriber line (DSL) from their telephone company. The cable and telephone companies are Bertrand competitors, but because changing providers is slightly costly (waiting for the cable repairman can eat up at least small amounts of time!), customers have some slight resistance to switching from one to another. The demand for cable Internet services is given by qC = 100 – 3pC + 2pT, where qC is the number of cable Internet subscribers in town, pC is the monthly price of cable Internet service, and pT is the price of a DSL line from the telephone company. The demand for DSL Internet service is similarly given by qT = 100 – 3pT + 2pC. Assume that both sellers can produce broadband service at zero marginal cost.
Derive the cable company’s reaction curve. Your answer should express pC as a function of pT.
Derive the telephone company’s reaction curve. Your answer should express pT as a function of pC.
Combine reaction functions to determine the price each competitor should charge. Then determine each competitor’s quantity and profits, assuming that the average total costs are zero.
Suppose that the cable company begins to offer slightly faster service than the telephone company, which alters demands for the two products. Now qC = 100 – 2pC + 3pT and qT = 100 –4pT + pC. Show what effect this increase in service has on the prices and profit of each competitor.
-
Consider two Bertrand competitors in the market for brie, François and Babette. The cheeses of François and Babette are differentiated, with the demand for François’s cheese given by qF = 30 – pF + pB , where qF is the quantity François sells, pF is the price François charges, and pB is the price charged by Babette. The demand for Babette’s cheese is similarly given as qB = 30 – pB + pF.
Find the Bertrand equilibrium prices and quantities for these two competitors.
Now consider a situation in which François sets his price first, and Babette responds. Follow procedures similar to those you used for Stackelberg quantity competition to solve for François’s profit-
maximizing price, quantity, and profit. Solve for Babette’s profit-
maximizing price, quantity, and profit. Was François’s attempt to seize the first-
mover advantage worthwhile?
There are only three big tobacco companies, but they produce dozens of brands of cigarettes. Compare and contrast Bertrand competition with undifferentiated and differentiated products to explain why the big three tobacco companies devote so many resources supporting so many different brands instead of producing just a single type of generic cigarette each. Do you think supporting all these different brands is good for society, or bad?
Consider a monopolistically competitive industry. A graph of demand and cost conditions for a typical firm is depicted in the diagram below:
Is this firm generating producer surplus? Is this firm earning a profit? How can you reconcile your answers?
464
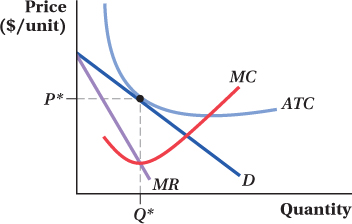
Do you expect any entry into or exit from this industry to occur? Explain.
Suppose that the government reduces annual licensing fees, causing the fixed cost of the typical firm to fall. Make appropriate shifts of all curves that might be affected. What happens to producer surplus? What happens to profit? Do you expect the fall in fixed costs to cause entry into or exit from this industry? Explain.
Shift the demand and marginal revenue curves to reflect the entry/exit you indicated in (c). Find the new equilibrium.
Continue to reduce fixed cost. What happens to the demand curve as fixed cost continues to fall? What happens to producer surplus and profit?
Find the equilibrium as fixed cost falls to zero.
One big question economics ponders is how to produce the greatest material well-
being using the fewest resources. Compare and contrast perfect competition and monopolistic competition in achieving that end. (Hint: You may want to consider a particular monopolistically competitive industry such as clothing or restaurant meals, and imagine what it would look like if it were perfectly competitive instead.) How does your answer depend on your definition of material well- being? When competition between firms is based on quantities (Cournot competition), the reaction functions we derive tell us that when Firm A increases its output, Firm B’s best response is to cut its own. However, when competition between firms is based on price (Bertrand competition), reaction functions tell us that Firm B’s response to a cut in Firm A’s price (which will lead to an increase in the quantity A sells) should be a corresponding cut in B’s price (and a corresponding increase in its own output). Reconcile these two results.
Suppose that the market demand for rose hip is given by P = 100 – Q. There are two firms, A and B, producing rose hip, each at a constant marginal and average total cost of $5. Fill in the table below for each market structure.
| Collusive Monopoly | Cournot Oligopoly | Bertrand Oligopoly | Stackelberg Oligopoly (A is first- |
|
|---|---|---|---|---|
| A’s Quantity | ||||
| B’s Quantity | ||||
| Industry Quantity | ||||
| Price | ||||
| A’s Profit | ||||
| B’s Profit | ||||
| Industry Profit |
| Collusive Monopoly | Cournot Oligopoly | Bertrand Oligopoly | Stackelberg Oligopoly (A is first- |
|
| A’s Quantity | 23.75 | 31.67 | 47.50 | 47.50 |
| B’s Quantity | 23.75 | 31.67 | 47.50 | 23.75 |
| Industry Quantity | 47.50 | 63.33 | 95 | 71.25 |
| Price | $52.50 | $36.67 | $5 | $28.75 |
| A’s Profit | $1,128.13 | $1,002.70 | $0 | $1,128.13 |
| B’s Profit | $1,128.13 | $1,002.70 | $0 | $564.06 |
| Industry Profit | $2,256.25 | $2,005.40 | $0 | $1,692.19 |
The Collusive Monopoly Case
Firms produce exactly the same output and sell it at the price where MC = MR, that is,
MR = 100 – 2Q = 5 = MC
Q = 47.50
Thus, each firm produces 23.75 units of output. The monopolistic price is
P = 100 – Q = $52.50
Both Firm A and Firm B generate the same profit, which is equal to
(P – ATC) × Q = ($52.50 – $5) × 23.75
= $1,128.13
The profit for the industry is $2,256.25.
The Cournot Oligopoly Case
The inverse demand function is
P = 100 – qA – qB
The residual marginal revenue for Firm i = {A, B} is
MR = 100 – 2qA – qB
Therefore, the reaction function for Firm i is
100 – 2qA – qB = 5
qA = 47.5 – 0.5qB
Therefore, the output produced by Firm A and Firm B is
q1 = 47.5 – 0.5q2 = 47.5 – 0.5(47.5 – 0.5q1)
= 23.75 + 0.25q1
qA = 31.67 = qB
The output for the industry is 63.33. The price is
P = 100 – qA – qB = $36.67
Both firms earn the same profit, which is equal to
(P – ATC) × Q = ($36.67 – $5) × 31.67
= $1,002.70
SB-
Hence, the profit for the industry is
$1,002.70 × 2 = $2,005.40
The Bertrand Oligopoly Case
Both firms will sell the product at the marginal cost of $5 and each will produce exactly the same quantity, that is,
5 = 100 – 2qi
qi = 47.50
Since firms sell output at the marginal cost, each firm’s profit is $0; thus, the industry profit is also equal to $0.
The Stackelberg Oligopoly Case
The reaction function for Firm B is
100 – qA – 2qB = 5
qB = 47.5 – 0.5qA
Assuming that Firm A is the first-
P = 100 – qA – qB = 100 – qA – 47.5 + 0.5qA
= 52.5 – 0.5qA
Equating the marginal revenue with marginal cost, the quantity produced by Firm A is
MR = 52.5 – qA = 5
qA = 47.50
Thus, Firm B produces
qB = 47.5 – 0.5qA = 47.5 – 0.5 × 47.5 = 23.75
The industry quantity is 71.25. The price is
P = 100 – qA – qB = $28.75
Firm A generates a profit of
(PA – ATCA) × QA = ($28.75 – $5) × 47.50
= $1,128.13
Firm B generates a profit of
(PB – ATCB) × QB = ($28.75 – $5) × 23.75
= $564.06
Thus, the industry’s profit is $1,692.19.
 Work this problem with calculus
Work this problem with calculus