12.2 Nash Equilibrium in One-Period Games
469
In Chapter 11, we had to expand the concept of equilibrium to apply it to market outcomes in oligopolistic industries. Because each oligopolistic firm’s price and quantity decisions influence those of its competitor, equilibrium in oligopolies requires more than just an equilibrium price and quantity for the industry as a whole. The stable market equilibrium also requires that no firm in the industry wants to change its decision given the choices its competitors are making.
A Nash equilibrium is a natural concept for determining the likely outcome of a game. In a Nash equilibrium, no player wants to unilaterally change her strategy given whatever strategies the other players are choosing. That is, the players are all doing the best they can, given the others’ actions.
Lots of dominated strategies in a game, as in the Warner Brothers–
normal form
The common organization of an economic game into its players, strategies, and the payoffs in a payoff matrix.
The first step to finding a Nash equilibrium in any game is to lay out the game’s players, strategies, and the payoffs that result from each combination of strategies. Table 12.1 does this for the Warner Brothers–
Let’s do an example with a new game. Two competing magazines, I’m Famous Weekly and Look at Me! Magazine, are each considering what to use as the cover story for its next issue. They each have the same two choices, which we’ll label reality show (RS) and celebrity interview (CI). We assume that neither magazine can observe its competitor’s cover choice until it’s on the newsstands, so both magazines must make their choices simultaneously. In addition, we assume some readers only like stories about reality shows, others only like celebrity interviews, and the readers who prefer celebrity interviews outnumber those who like reality show articles. If a magazine is the only one offering a particular type of story, it will get all of those readers. If both offer the same story, they will split those readers between them, but Famous will receive a larger share than Me! because a majority of readers prefer Famous, all else equal.
The profits (in thousands of dollars) that each magazine earns depend on its own choice for a cover story as well as its competitor’s choice. These choices and their payoffs are shown in Table 12.2. As before, the red number before the comma in each cell is the payoff to I’m Famous Weekly, and the blue number after the comma is the payoff to Look at Me! Magazine.
To zero in on the game’s Nash equilibrium, let’s first consider Famous’ best responses to Me!’s possible actions. If Me! chooses an RS cover story (left column), then Famous’ best action is to choose a CI cover. This is because it will earn a $500,000 payoff by choosing CI but only $300,000 by choosing RS. To keep track of this best response, we’ll put a check next to Famous’ payoff in the bottom left cell. If Me! runs a CI cover, Famous’ best response is still to choose CI because it earns $450,000 instead of $400,000. Because this is Famous’ best response in this situation, we put another check next to the $450. We can see that choosing a celebrity interview as its cover story is a dominant strategy for Famous; no matter what Me! does, Famous makes more money by going with the CI cover.

*Payoffs are measured in thousands of dollars of profit.
470
Now let’s do the same exercise for Me!. If Famous chooses a reality show cover, then Me! should choose a celebrity interview cover, because it will make $400,000 of profit rather than $0. We put a check next to the $400 payoff in the upper-
Looking at the pattern of checks (i.e., the pattern of best-
Me! Magazine, on the other hand, has no dominant strategy: If Famous chooses an RS cover, then Me! is better off choosing CI. If Famous instead chooses a CI cover, Me! will earn a higher profit by choosing a reality show cover. Thus, Me!’s best strategy changes with the choice made by Famous; no one strategy is best under all circumstances, so Me! has no dominant strategy. It also has no dominated strategy because both strategies (RS and CI) can each be a best strategy for Me!, depending on Famous’ action.
Second, even though we can’t eliminate many possible outcomes by getting rid of dominated strategies, there is still a Nash equilibrium to the game. In fact, we can see that Famous choosing a CI cover story and Me! choosing an RS cover are a mutual best response—
471
make the grade
The check method
Solving games can be challenging and complicated. But there are ways to simplify games that will make you a Nash equilibrium expert in no time!
To begin, always look at each player’s decision-
Let’s start by considering how Row should form her strategy:
First, ask, “If Column chooses action A, what is the best action for Row to take?” Then place a check mark next to the payoff for that action for Row. Row’s payoffs should always be to the left of the comma in payoff matrices.
Next, ask, “If Column chooses action B, what is the best action for Row to take?” Then place a check mark next to that option.
Second, repeat the exercise from Column’s perspective:
First, ask, “If Row chooses A, what is the best action for Column to take?” Check mark that payoff. (Remember that Column’s payoffs should always be to the right of the comma in payoff matrices.)
Next, ask, “If Row chooses B, what is the best action for Column to take?” Another check mark.
Once you have finished looking at the game from both players’ perspectives, look at all of the boxes in the payoff matrix. Do any have two check marks? If so, those are Nash equilibria. However, if none have double check marks, then the game does not have a Nash equilibrium (at least in pure strategies, covered later in this section).
The following sample game illustrates this method at work. (We print the payoff matrix in black ink rather than red and blue, so you can see what a matrix will look like on an assignment or exam.)
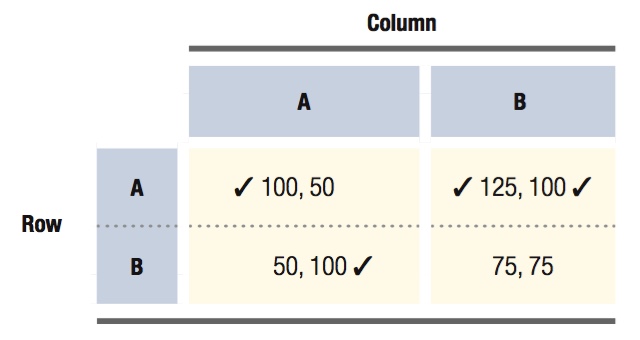
First, we look at Row’s choices. If Column chooses action A, Row is better off choosing A (100 > 50). If Column chooses action B, Row is once again better off choosing action A (125 > 75). Therefore, we place check marks next to both of Row’s payoffs from choosing A.
Next, we look at Column’s choices. If Row chooses action A, Column is better off choosing B (100 > 50). If Row chooses action B, however, Column is better off choosing A (100 > 75). We place check marks next to these payoffs.
Note that there is only one box in the payoff matrix in which two check marks appear: Row selecting A and Column choosing B. This is the Nash equilibrium of the game.
You can also use this method to look for dominant and dominated strategies for each player. A dominant strategy is a strategy that is best for a player no matter what action the other player takes. Consider Row’s decision we described above. If her answer to both questions is the same (always choose action A no matter what action Column takes or always choose B no matter what action Column takes), that strategy is a dominant strategy. You can then cross out the alternative (dominated) strategy, allowing you to reduce the game to fewer options. Then, repeat the process for Column. Crossing out can only occur when there are dominated strategies. When using the check method, dominated strategies are indicated by rows or columns without any check marks.
Remember that following dominant strategies will lead to a Nash equilibrium but not all Nash equilibria involve dominant strategies. Here is an easy way to tell the difference (again using our example from above):
Row: “Column, I don’t care what you do! No matter what action you take, I am always better off choosing action A.” (In other words, Row has a dominant strategy.)
Column: “Row, your choice influences my best option. Given that you are choosing action A, I am better off choosing action B.” (Column has no dominant strategy, but choosing B when Row chooses A is the best response.)
Practice these steps, and game theory will no longer be a mystery to you!
472
figure it out 12.1
For interactive, step-
Two grocery stores in a small city are considering ways to update their stores. Each store can build a new store, remodel its existing store, or leave its store in its current condition. The game is shown below. Food4U’s payoffs are listed before the comma and Grocery Mart’s after. Payoffs listed are the stores’ annual profits in thousands of dollars.
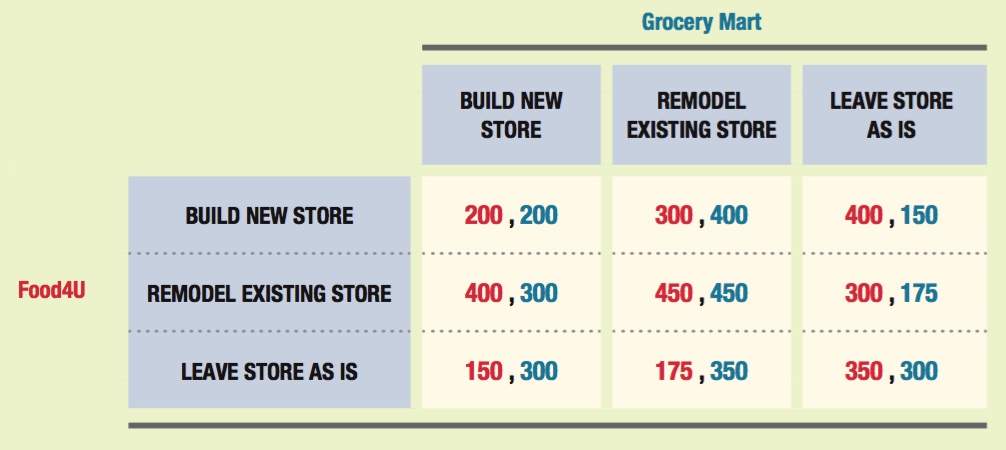
Are there any dominant strategies for either Food4U or Grocery Mart? Explain.
Are there any dominated strategies for either Food4U or Grocery Mart? Explain.
Solve for any Nash equilibria.
Solution:
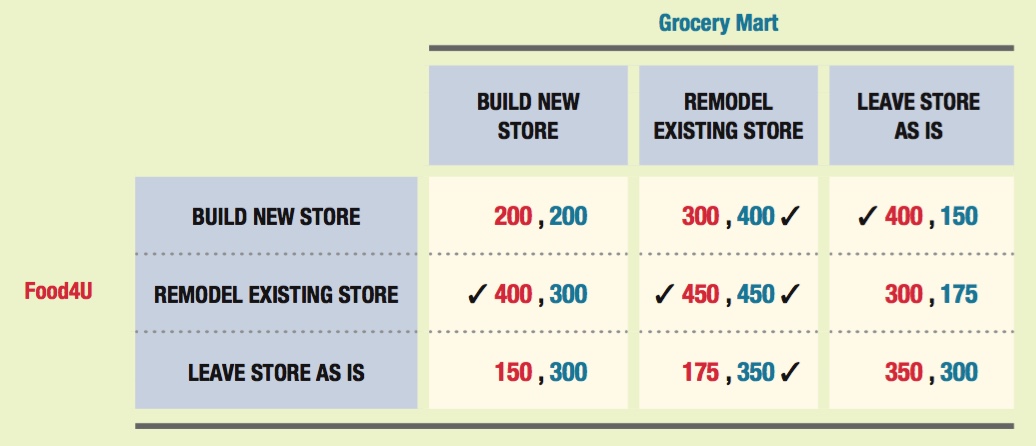
A dominant strategy is a strategy that is best for a player no matter what strategy its opponent follows. Let’s begin with the decision for Food4U. If it believes that Grocery Mart will build a new store, Food4U will remodel its existing store ($400,000 > other payoffs when Grocery Mart builds a new store). If Food4U believes that Grocery Mart will remodel its existing store, it will also remodel its existing store ($450,000 > other payoffs). But, if Food4U believes that Grocery Mart will leave its store as it currently stands, Food4U will build a new store ($400,000 > other payoffs). Because no strategy is the best to follow no matter what Grocery Mart does, Food4U does not have a dominant strategy.
Now, let’s examine the decision for Grocery Mart. If Grocery Mart believes that Food4U will build a new store, its best strategy would be to remodel its existing store ($400,000 > other payoffs). If Grocery Mart thinks that Food4U will remodel its store, Grocery Mart’s best strategy is to also remodel its own store ($450,000 > other payoffs). And, if Grocery Mart believes that Food4U will leave its own store as it is, Grocery Mart will still want to remodel its own store ($350,000 > other payoffs). Therefore, remodeling its store is a dominant strategy for Grocery Mart because it is the best strategy for Grocery Mart to follow regardless of the strategy Food4U chooses.
When Food4U believes that Grocery Mart will either build a new store or remodel its current store, Food4U’s best strategy is to remodel its own store. When Food4U believes that Grocery Mart will leave its own store in its current state, Food4U is better off building a new store. This means that under no circumstances is it better for Food4U to leave its store as is. Thus, “Leave Store As Is” is a dominated strategy for Food4U. Because “Remodel Existing Store” is a dominant strategy for Grocery Mart, the other two strategies must be dominated strategies for Grocery Mart.
473
Using the check method (shown in the table below), we can see that the Nash equilibrium occurs when Food4U and Grocery Mart both remodel their stores. This makes sense because “Remodel Existing Store” is a dominant strategy for Grocery Mart, and when Grocery Mart remodels its store, Food4U is also better off remodeling its own store.
Multiple Equilibria
Predicting likely outcomes of a game can be fairly easy when there’s only one Nash equilibrium, as there is with prisoners’ dilemmas or with the magazine cover story game we just analyzed. Because of the mutual-
Let’s revisit Warner Brothers and Disney, but this time we look at their choice of when to release their next movies. Suppose that both companies currently have animated movies ready for distribution, so now they must decide when these movies should open in theaters around the country.
Both companies want to take advantage of certain periods of the year when people have especially high demand for watching movies. Let’s simplify things by saying the companies basically have three periods from which to choose their opening date. One is the Memorial Day weekend (which we’ll call May). This is traditionally a big movie-
Warner Brothers and Disney both understand these demand patterns. And if either were a monopolist, it could easily rank its opening date choices: May is best, then December, then March. But they’re not monopolists. Their profits from choosing a particular opening date will depend on the other company’s choice as well. This is, then, a game theory problem. The two companies realize that if they both choose the same opening date, it will be a disaster. They’ll split the animated feature market down the middle rather than having the whole market to themselves (though at different times in the year).
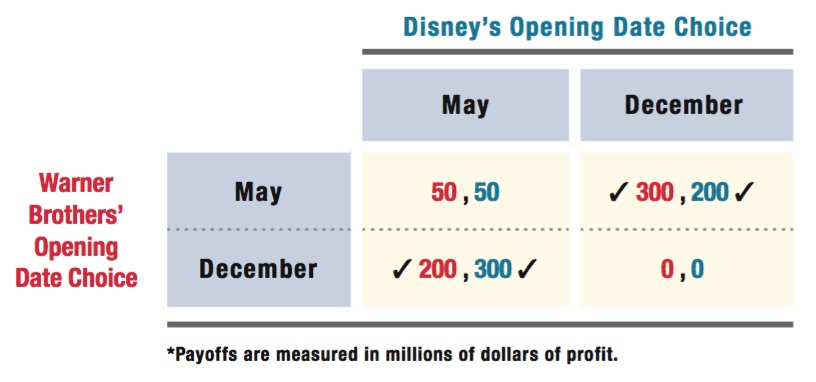
So how will Warner Brothers and Disney balance these opposing considerations? Table 12.3 shows the specifics of the game they are playing, including the payouts that both companies would receive for any possible set of opening date strategies.
474
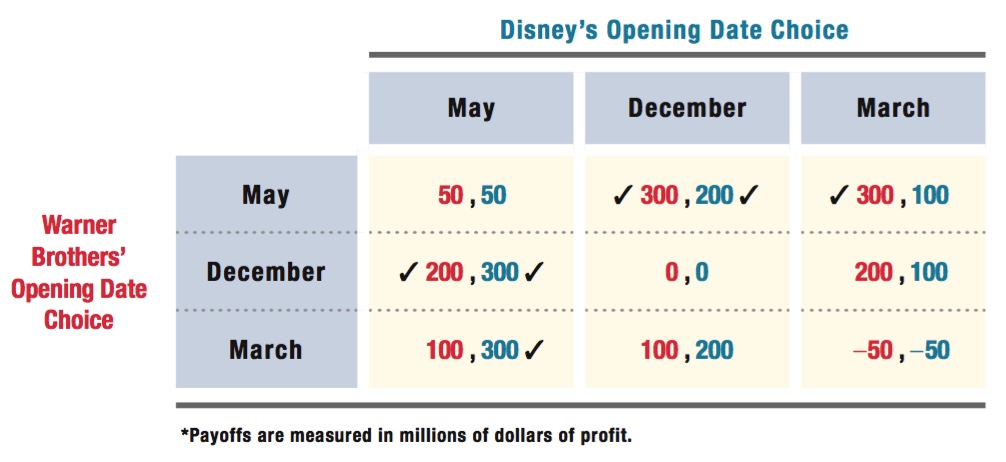
*Payoffs are measured in millions of dollars of profit.
If either company chooses a May opening when the other does not, the May opener makes $300 million. If either company opens by itself in December, its movie will make $200 million. Finally, if either company has a March opener to itself, it makes $100 million.
If both companies open their movies in the same month, however, neither fares so well. In fact, we assume they’ll earn lower profit regardless of the opening date (although they’ll lose more if they open during worse times of the year). If they both choose to open in May, they make only $50 million each. If both movies open in December, each company earns zero profit. And if both firms opt to open in March, they will each incur a $50 million loss.
What is the Nash equilibrium for this game? To find out, we apply our box-
Everything for Disney’s optimal responses is just a mirror image, so we can check off its best responses in the same manner. If Warner Brothers chooses a May opening date, Disney should choose December ($200 million is its largest payoff possible; top cell of middle column). If Warner Brothers chooses either a December or March opening date, Disney earns more profit by choosing May ($300 million is its largest payoff possible; middle and bottom cells of the left column).
Now we’ve identified each firm’s best responses to any possible strategy its competitor might pursue. Notice that a March opening is a dominated strategy for both players. That is, it is never optimal to open in March regardless of what the competitor might do. So we can ignore any outcomes that involve either firm opening in March. That simplifies the game to the four squares in the upper left of the game table. These are shown by themselves in Table 12.4.
Look at the mutual best responses, where there are two checks in the same box. There are two of them. Either Warner Brothers picks December and Disney chooses May, or the other way around. Both outcomes are Nash equilibria of the game. This game shows the difficulty of predicting the outcome of games with multiple equilibria. We can narrow down the possibilities—
475
*Payoffs are measured in millions of dollars of profit.
Later in the chapter, we see that changes in the structure of the game, such as changes in the sequence of moves or modest shifts in payouts, can lead to different outcomes than the multiple Nash equilibria shown here. For the time being, however, we’ve gone as far as game theory can take us with this game.
Mixed Strategies
pure strategy
A strategy in which the player chooses a particular action with certainty.
mixed strategy
A strategy in which the player randomizes her actions.
We have been focusing on games in which a player makes a choice between different actions, choosing the specific strategy that maximizes her payoff. This type of strategy is known as a pure strategy. However, it may not always be in the player’s best interest to follow a pure strategy. In some situations, it may be best for the player to choose her actions randomly from the set of pure strategies available to her. This type of strategy is called a mixed strategy.
As an example of a game that can be played using a mixed strategy, think of a soccer game in which a player is taking a penalty kick. You’ve probably seen this on TV, or perhaps done it yourself on the field. The kicker faces the goalie, alone, and kicks the ball from close range. The distance is so close, in fact, that the goalie just dives to one side or the other and prays that it’s the right way. It turns out that penalty kicks can be analyzed using game theory. There are two players (the kicker and the goalie), with each having a set of strategy choices (“kick left” or “kick right” for the kicker, “dive left” or “dive right” for the goalie), and payoffs that depend on the chosen strategies of both players. This game is shown in Table 12.5.
Let’s assume we’re considering a pivotal penalty kick: If the goalie picks the same side as the kicker, the goalie’s team wins, and if the players choose opposite sides, the kicker’s team wins. We can assign payoffs of 1 to the winner and 0 to the loser. That’s what is shown in the table. Note that, because the kicker and goalie face each other, a kicker choosing to kick to the right will hope that the goalie dives to the left—
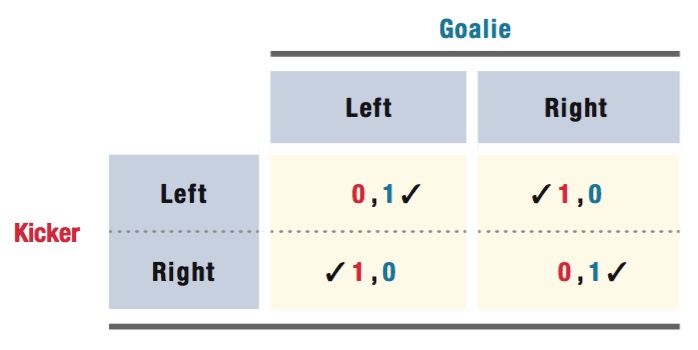
Let’s use our check method again. The kicker always wants to do the opposite of what the goalie does. If the goalie chooses left, the kicker’s best response is to choose right. If the goalie dives right, the kicker wants to kick left. However, the goalie always wants to match the kicker’s choice: If the kicker chooses left, the goalie’s best response is to go left and go right if the kicker chooses right. Putting checks by all these responses gives us the situation in the table.
476
Notice what has happened: There is no box with two checks in it. That’s because no set of strategies exists such that both players simultaneously choose the best response to the other’s choice. Given what one player chooses, the other player will want to switch. Our check method therefore doesn’t indicate any pure-
There actually is a Nash equilibrium to this game, but it is not one in pure strategies in which each player chooses a single action. Up to now, the games we’ve analyzed have had at least one (and sometimes more) pure-
The Nash equilibrium that exists in the penalty-
Although the 80/20 right/left strategy example above is a mixed strategy, it is not a Nash equilibrium strategy. Think about it: If the kicker is going right 80% of the time, then the goalie’s best response is to always go right. But the kicker’s best response to a goalie diving right every time is to kick left all of the time. But if the kicker always goes left, the goalie also wants to go left all the time. If they want to switch once they know what the other player is doing, it’s not a Nash equilibrium.
The only mixed-
The strange thing about a mixed-
Application: Random Mixed Strategies in Soccer
One of this book’s authors, Steven Levitt, researched whether soccer players used mixed strategies when they take penalty kicks as we just described. Along with his coauthors Pierre-
477
They classified kickers’ and goalies’ choices into one of three strategies: left, right, and center. This is a bit more complicated than the left/right example, but the logic of the analysis was the same: The Nash equilibrium theory says that kickers and goalies should randomize across the choices in a way that makes the observed success rates of any direction choice the same.

This is just what Levitt, Chiappori, and Groseclose found in the actual data. The kickers and goalies seem to randomize their choices almost perfectly. The success rate was basically identical no matter which way they went. Chalk up a victory for game theory! It predicted very well the behavior of these players—
The funny side story of this research involves one hapless player who didn’t quite figure out how randomized strategies work. When we talk about mixed strategies involving randomizing across strategies with certain probabilities, we mean randomizing. It’s more than just making sure that one-
Evidently, truly randomizing was too difficult for this player. So, he followed a set pattern for his kicks: first left, then center, then right, then back to left, and so on. He figured that mixing equally across the three choices would be enough to make goalies randomize in response. But it didn’t take too long for the goalies to figure out his system. They started blocking virtually all of his kicks. This player may not know microeconomics, but he still learned (the hard way) that in soccer, there is no pure-
What If My Opponent Is an Idiot? The Maximin Strategy
In game theory, the idea of Nash equilibrium is based on players rationally considering all the possible payoffs and coldly calculating their optimal best responses to their opponent’s choices. You can probably imagine, then, that the notion of players making systematic errors (errors that are nonrandom and occur over and over again in the same direction) poses a big problem for predicting the outcomes of games by looking for Nash equilibria. If a player cannot trust her opponents to at least do what’s in the opponents’ best interests, how should she act?
In Chapter 18, we look at some of the new economic research on behavioral economics, the branch of economics that argues people don’t always behave rationally and often make various systematic errors in judgment.
maximin strategy
A strategy in which the player minimizes her exposure to loss.
We have a lot to say about irrationality in Chapter 18, but now is a good time to bring up a type of strategy known in game theory as the maximin strategy (short for “maximize the minimum”). Maximin is a conservative strategy because the player is not going for the highest payoff, but is instead choosing a strategy to minimize losses. Therefore, maximin can be useful in games in which one or more players might be irrational. The idea of the maximin strategy (and the origin of its name) is that a player takes actions that minimize the damage to her in the worst-
478
*Payoffs are measured in thousands of dollars of profit.
Let’s go back to our earlier example in which two magazines are choosing a cover story for their next issue. We saw that a celebrity interview (CI) cover story was a dominant strategy for I’m Famous Weekly, and that the Nash equilibrium had Look at Me! Magazine going with a reality show (RS) cover as a best response. The payoffs are shown in Table 12.6 (which is the same as Table 12.2).

But suppose for a minute that Me!’s management believes its competitor isn’t just Famous but also dumb—
If Me! is risk-
Something that’s interesting to note about this sort of situation is that a firm might realize it can influence its competitor’s behavior by seeming to be crazy. The mere threat of irrational behavior—
Application: Fun in the Sun: Wine Making for Irrational Billionaires
Ah, owning a vineyard—
If you simplify the business of wine making, you can think of two basic types of product: high-
479
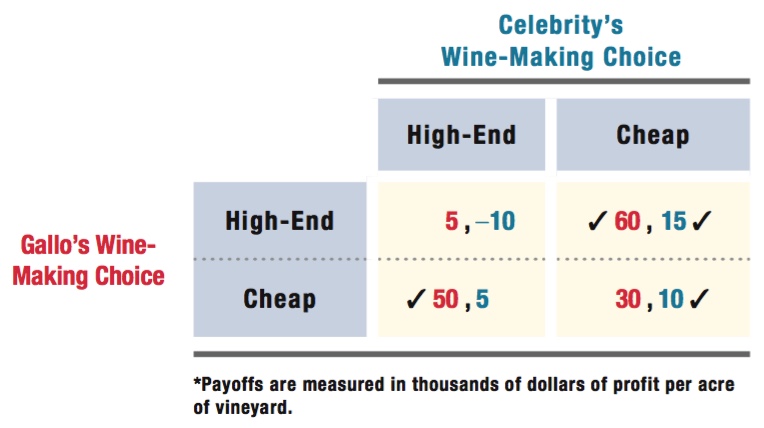
If both the celebrity and Gallo decide to produce the same type of wine, Gallo will make a larger profit because of its relative expertise. In fact, the celebrity might be expected to lose money if both make high-
Let’s look at the players’ best responses, shown by the checks. We can see that the Nash equilibrium has Gallo making high-
If the celebrities think like game theorists, they’ll realize this. So, Gallo ought to be able to count on celebrities making cheap wine, in which case Gallo should make high-
If Gallo suspects that the celebrities might be committed to producing high-
This example comes straight from microeconomic research done by Fiona Scott Morton and Joel Podolny.2 Their study of the wine industry documents an extremely large amount of entry into the high-