12 Game Theory

12.4 Sequential Games

sequential games

Games where one player moves first and other players observe this action before making their decisions.

There are many situations in which players do not have to make their moves at the same time, as we’ve been assuming so far. Instead, they take actions in turn. One player moves first, and the other observes this action before making her decision. Games with this structure are known as sequential games.

486

extensive form or decision tree

Representation of a sequential game that shows both the choice and timing of players’ actions.

The normal-form matrix that we’ve been using for simultaneous games doesn’t work for sequential games, because it does not provide us with a way to keep the timing of actions separate from the choice of actions. Instead, we plot sequential games in what’s called the extensive form or a decision tree (Figure 12.2). The sequence of the game flows from left to right. Each node in an extensive form game represents a choice, and the player listed at that node is the one choosing what action to take. The payoffs to every possible sequence of strategies are listed at the far right.

Figure 12.2: FIGURE 12.2 Decision Tree for Choosing a Release Date

Figure 12.2: In this sequential game, Warner Brothers chooses a release date first at node A. If Warner Brothers chooses a May release date, Disney will choose a December release date at node B; if Warner Brothers chooses December or March, Disney will choose May at nodes C and D, respectively. Unlike the simultaneous game outcome in Table 12.4, the companies reach a single Nash equilibrium at node B. Here, Warner Brothers releases The LEGO Movie 2 in May, and Disney releases Frozen 2 in December.

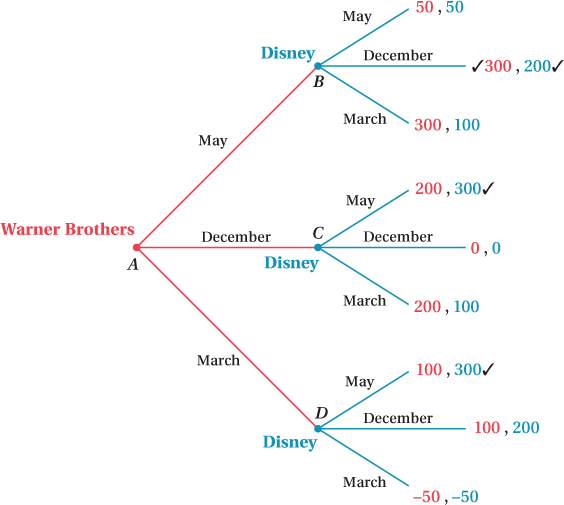
Figure 12.2 revisits the Warner Brothers–Disney release date game we presented earlier in Table 12.3 (which we repeat as Table 12.9 for convenience) as a game in which both firms make their decisions at the same time. Now we assume that Warner Brothers finishes The LEGO Movie 2 first and gets to choose a release date before Disney chooses one for Frozen 2.

The leftmost node (A) in the decision tree represents Warner Brothers’ opening date choice. Once it has decided, then Disney can choose. If Warner Brothers chooses a May opening date, then Disney makes its choice from node B. If Warner Brothers instead chooses December, then Disney decides from node C. For a Warner Brothers opening choice of March, Disney responds from node D.

Depending on two firms’ choices, the firms earn the payoffs listed on the far right. [As in the normal form game, the first number listed in each pair (red) is Warner Brothers’ profit, and the second number (blue) is Disney’s profit.] If you look at these payoffs for a minute, you can see that we’ve just transformed the normal form game payoffs in Table 12.9 into extensive form for this sequential game. When one firm moves first, however, as Warner Brothers does here, the outcome of the game is completely different. When the game was a simultaneous-move game, we found that there were two pure strategy Nash equilibria: (1) Warner Brothers releases in May for a profit of $300 million, and Disney releases in December for a profit of $200 million and (2) Warner Brothers releases in December for a profit of $200 million, and Disney releases in May for a profit of $300 million. What happens in a sequential game?

487

Table 12.9 Selecting a Release Date*

Just as we did in the repeated simultaneous games in Section 12.3, we use backward induction to find Nash equilibria in sequential games. Suppose Warner Brothers picks May. That puts us at node B in the game tree, and Disney must now choose an opening date in response. If Disney also chooses May, it will make $50 million. If it chooses December, its profit will be $200 million. If it chooses March, it will earn $100 million. Therefore, the best response Disney can make is to choose December, and we put a check next to Disney’s December payout in the figure.

Now suppose Warner Brothers picks a December opening instead, putting the game at node C. Going through the same process, we see that if Disney chooses May, it earns $300 million. It now makes zero profit by going with December and earns $100 million with a March opening. Disney’s best response to Warner Brothers’ choice of December is to open in May, so we check this choice.

Finally, if Warner Brothers chooses to open its film in March (node D), Disney will open in May. It earns $300 million by doing so instead of earning only $200 million with a December opening and losing $50 million with a March opening. Again, we put a check by the May opening choice.

Now that we know how Disney will respond in the last stage for all possible first moves by Warner Brothers, we can work backward to figure out exactly what choice Warner Brothes will make at the first node (A). Warner Brothers understands how Disney will respond to each of its possible strategy choices and can make its own decision based on these expected responses. If Warner Brothers chooses a May opening, for example, it knows that Disney maximizes its own profit by choosing a December opening.

Here is how Warner Brothers looks at its choice in the first stage. If it chooses May, Disney will open in December, and Warner Brothers will earn $300 million. If Warner Brothers opens in December, Disney will respond by opening in May, and Warner Brothers will earn $200 million. Finally, Warner Brothers earns $100 million with a March opening because Disney will respond with a May opening. It is clear that Warner Brothers’ highest payout, $300 million, occurs when it chooses a May opening date, and we put a check next to that payoff.

488

That’s it; we have an equilibrium of the sequential game. The LEGO Movie 2 opens in May and Frozen 2 opens in December. Warner Brothers earns $300 million in profit and Disney makes $200 million. In the simultaneous-move game, we had multiple equilibria; either firm could open in May and the other in December. But when the firms act sequentially, the firm that chooses first gets the lucrative May slot. The sequential structure eliminates the multiple equilibria problem that can occur with simultaneous games. The outcome is still a Nash equilibrium, though. Taking the other player’s action as given, each player is doing the best it can once its turn rolls around.

It’s important to realize that we just arbitrarily picked Warner Brothers as the first-mover in playing this game. If we look at the structure of the game’s payouts for a minute, it should be apparent that if Disney were able to choose first, the equilibrium would be reversed: Disney would open in May (earning $300 million) and Warner Brothers would open in December (earning $200 million). This outcome raises a few questions. What factors would determine which firm is the first-mover in the real world? If it wasn’t clear who would make the first move in a sequential game, could a firm just be the first to threaten to open in May and gain the first-mover advantage? Is moving first always an advantage in a sequential game? We look at these sorts of questions in the next section.

Backward induction and trimming trees

Solving sequential games requires you to work backward, using a technique that game theorists call backward induction. It may seem a little strange to start with the second player when you know that the second player must wait until the first player makes her move. After all, the whole point of a sequential game is that the order of plays is important, and often the first player has a first-mover advantage. So, why would we start solving the game from the end and work backward?

Remember that we assume all players know the strategies available to every player in the game and the payoffs that accompany every possible outcome. Before Player 1 decides her strategy, she must consider what Player 2 is likely to do. After all, Player 1’s payoff is determined both by her choice and that of her opponent. When we are solving the game, we want to think like the players. Therefore, to determine the best strategy for Player 1 to use, we must first examine what Player 2 is likely to do given every possible choice that Player 1 might choose. While it seems like we are acting as if Player 2 is moving first, in reality we are just putting ourselves in Player 1’s shoes as she considers her best strategy, and that begins with predicting Player 2’s moves.

There is another useful step, called “trimming the branches,” that you can take to simplify sequential games. (This term comes from the idea that the extensive form of a game is often referred to as a “decision tree.”) Trimming the branches is very similar to removing dominated strategies in a normal-form game. Basically, this method allows you to narrow the solution options by eliminating any branches that represent any actions that Player 2 would never take.

489

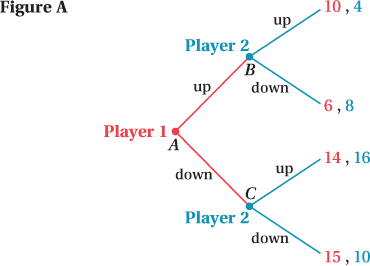
We can use backward induction to solve the game shown in Figure A. Remember, we are trying to think like Player 1—who is moving first—in considering what Player 2 will do. Look at node B, where Player 1 has selected “up.” What will Player 2 do? He will choose “down,” because his payoff is greater. Not only can we add a check mark to that payoff, but we can also eliminate “up” as an option at node B (because Player 2 will not choose it). Therefore, we can trim (mark out) that branch as shown in Figure B. Now, consider what Player 2 will do if Player 1 chooses “down” (node C). Here, Player 2 will choose “up,” so we can put a check mark next to that payoff and mark out the “down” branch at node C.

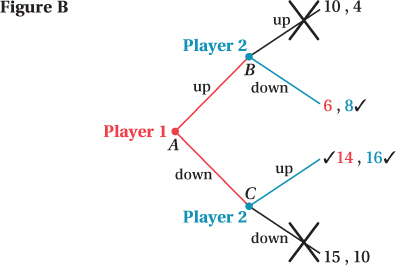
The final step we must take is choosing Player 1’s best strategy. She knows that, given Player 2’s expected moves, she is only left with two options (those not trimmed from the tree): Choose “up” and earn a payoff of 6, or choose “down” and earn a payoff of 14. Therefore, she will choose “down” and we can place a check mark by her payoff.

Backward induction and trimming the tree greatly simplify even the most complex sequential games. The trick is to place yourself in the first player’s shoes by considering the actions that will be chosen by the second (third, fourth, etc.) player. Sometimes it is beneficial to do things backward!

Another Sequential Game

Let’s close this section by considering another sequential game. Here’s how it works.

Suppose that Dan and Patrick are two contestants on a game show called “Play or Pass.” They flip a coin to decide who goes first, and Dan wins. The rules are simple: Dan decides if he wants to play or pass. If Dan chooses “Play,” the game ends and he receives a payoff of 1, and Patrick receives a payoff of –10. However, if Dan chooses “Pass,” then Patrick gets a turn. If Patrick chooses “Play,” he receives a payoff of 12 and Dan receives a payoff of 0. If Patrick chooses “Pass,” however, both players receive a payoff of 11. This sequential game is shown in Figure 12.3. Dan’s decision occurs at node A, and Patrick’s at node B.

Figure 12.3: FIGURE 12.3 Sequential “Play or Pass” Game

Figure 12.3: In the “Play or Pass” game, Dan must first decide whether to choose “Play” or “Pass” (node A). If Dan calls “Play,” he earns a payoff of 1 and Patrick loses 10. If Dan decides to opt for “Pass,” Patrick will choose “Play” at node B, yielding Dan a payoff of zero and Patrick a payoff of 12. Therefore, at the Nash equilibrium, Dan will choose “Play” and earn 1.

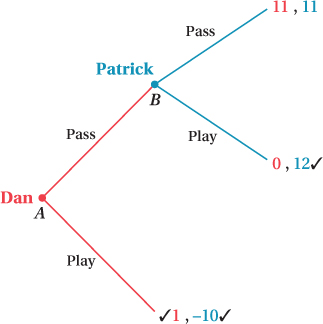
Before we solve for the equilibrium of this game, let’s look at all the possible payoffs. One outcome—which occurs if both Dan and Patrick call “Pass”—results in high payoffs for both players, with each getting 11. The other two outcomes are lopsided: If Dan calls “Play” immediately, the game ends with him earning a payoff of 1 and Patrick losing 10. If Dan instead calls “Pass” and Patrick responds with “Play,” the game ends with Patrick earning 12 and Dan obtaining nothing. You might think that a game structure like this gives the players a strong incentive to get to the pass/pass outcome, so that both can receive a positive payoff. Let’s use backward induction to see if this prediction is correct.

490

At node B, Patrick can call “Play” and earn 12 or call “Pass” and earn 11. Because the higher payoff comes from choosing “Play,” Patrick will choose that. Knowing that Patrick will choose “Play” if he gets a turn, Dan will call “Play” at node A and earn 1. (If for some reason Dan calls “Pass,” he knows he will earn a payoff of 0.) Faced with this choice, it’s clear that Dan does better by calling “Play” and ending the game right off the bat. Therefore, the equilibrium payoffs are 1 for Dan and –10 for Patrick.

This equilibrium probably wasn’t obvious to you just from our initial look at the game’s structure and payoffs. The example shows how backward induction can provide help beyond intuition alone when determining the outcomes of sequential games. The example also demonstrates the value of actions that players might take to change the structure of a game in a favorable way. We talk about these sorts of actions in the next section.

See the problem worked out using calculus

figure it out 12.3

Two firms, GamesRUs (GRU) and PlayThings Incorporated (PTI), are considering a new television advertising campaign for their Christmas gift registries. Because television advertising is expensive, each firm earns greater profit ($50 million) when it does not advertise. If both choose to advertise, very few new customers are gained and each firm earns only $30 million profit. However, if one firm advertises while the other does not, the firm choosing to advertise gets the majority of customers, earning a profit of $70 million, while its competitor only earns $20 million profit.

Create a table showing the normal form of this game.
List all Nash equilibria.
If this game is played sequentially and GRU makes its decision before PTI, what will the outcome be?
Is there a first-mover advantage in this case? Explain.

Solution:

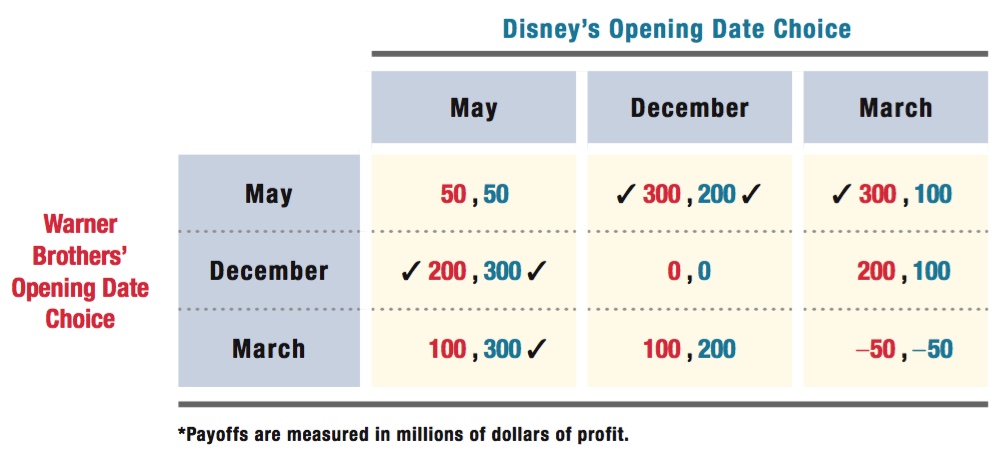
The normal form is shown below (payoffs are in millions of dollars with GRU’s profits before the comma and PTI’s after):
We can use the check method to determine the Nash equilibria. If GRU believes that PTI will advertise, its best move is to also advertise ($30 million > $20 million). If GRU believes that PTI will not advertise, its best move is to advertise ($70 million > $50 million). Therefore, advertising is a dominant strategy for GamesRUs because it is the best strategy no matter what strategy PlayThings Inc. follows. Note, too, that because PTI’s payoffs are the same as those of GRU’s, advertising is also a dominant strategy for PTI. Therefore, we end up with the following:

491

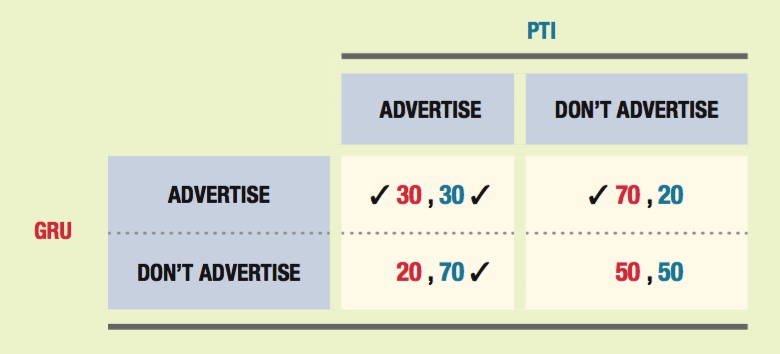
Because advertising is a dominant strategy for both firms, the outcome of this game is found in the upper-left portion of the payoff matrix and each firm earns a profit of $30 million. This is the Nash equilibrium because neither firm has an incentive to change its strategy given the strategy of the other.
The extensive form of this game (with GamesRUs moving first) is shown in the figure below:

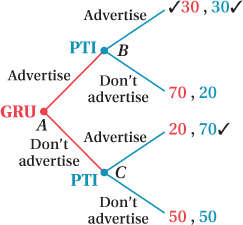
Using backward induction, we can see that, when GRU chooses to advertise, PTI will also choose to advertise (because $30 million > $20 million). If GRU chooses not to advertise, PTI will still choose to advertise (because $70 million > $50 million). Therefore, if GRU understands how PTI will respond to its strategy, it will also choose to advertise (because $30 million > $20 million).
No first-mover advantage exists in this case because both firms have dominant strategies. A dominant strategy is the best strategy to follow no matter what your opponent does. Therefore, it is irrelevant if one firm makes its decision before the other firm; each firm will always choose its dominant strategy: to advertise.