14.2 Evaluating Investment Choices
Now that we’ve covered the basics of present discounted value analysis, we can apply that framework to evaluate investment choices.
Net Present Value
In Section 14.1, all the payments had the same sign. That is, the individual payments have all been considered proceeds for whoever owns the payment stream. But, there are many cases in which some payments are benefits and others are costs. Investment projects, for example, usually have up-
Let’s suppose you go skiing a few times a year and are considering buying your own skis to save the hassle and cost of renting them. You have found a pair you like that costs $500, and you expect to use them for the next three years. You figure out that you typically spend $200 a year on rental skis. Thus, there are three $200 benefit payments: one a year from now, another in two years, and a third in three years. (For simplicity, assume that the $200 benefit comes in one payment at the end of the season.) The payoff structure of the skis purchase is shown in Table 14.1. Should you buy the skis or continue renting?
The first thing to do is figure out the present discounted value of the investment in your own pair of skis. Applying the PDV formula, we have
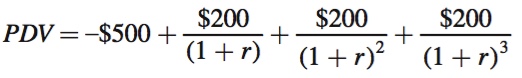
The first term is the cost of buying the skis. It happens in the present period, so it is not discounted. Because it is a cost to the decision maker rather than a benefit, it is negative. The other terms account for the future benefits of buying the skis. They have positive signs and are discounted based on how far into the future they occur.
As we have seen in our examples, the PDV of this potential investment also depends on the interest rate. If r = 4%, the PDV of buying the skis is $55.02:
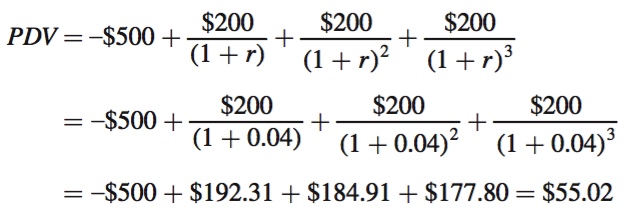
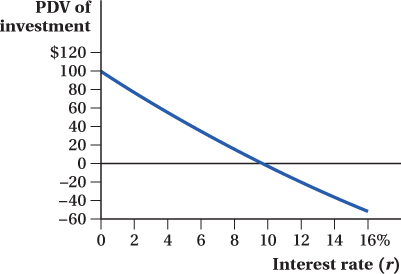
This positive number implies that at a 4% interest rate, the skis’ future benefits outweigh their cost in present value terms, so buying them is a worthwhile idea. If the interest rate is 2% instead, the net PDV is larger: $76.78, an even stronger case for buying the skis. However, if r is higher than 4%, the PDV is less than $55.02. In fact, if r is high enough, the net PDV will be negative. At a 10% interest rate, for example, the PDV is –$2.63; that is, buying the skis creates a loss of $2.63 in present value terms. At an interest rate of 10%, the present value of the skis’ future benefits does not make up for their up-
549
net present value (NPV) analysis
The use of the present discounted value to evaluate the expected long-
Using PDV to evaluate the return of a proposed investment (as we just did in our skis example) is sometimes called net present value (NPV) analysis, a method of evaluating investment projects that uses present discounted value to put all of an investment project’s future cost and benefit flows on a common basis, so they can be compared apples-
We can extend the NPV analysis method to more complex costs and benefits payment streams. Costs incurred in the future rather than the present have negative signs and are discounted just like any other payments. Because costs and benefits that occur in the same period are discounted equally, they can first be combined into a net benefit for each period. If costs outweigh benefits, the net benefit is negative; if benefits outweigh costs, the net benefit is positive. Once the PDVs of all net benefits are computed, they are added together to obtain the net present value.
This procedure gives us the generic formula for computing the NPV of any investment decision. Label the periods spanned by the investment project 0, 1, 2, . . . , T, where 0 is the current period and T is the last period in which any costs or benefits associated with the project occur. B0, B1, . . . , BT are the investment’s benefits in the respective periods and C0, C1, . . . , CT are the costs. The NPV formula is
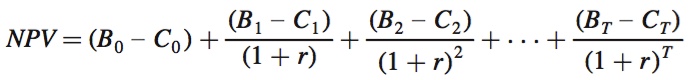
where Bt – Ct is the net benefit in any particular period t. In our ski purchase example, T = 3, B0 = $0, B1 = B2 = B3 = $200, C0 = $500, and C1 = C2 = C3 = $0:
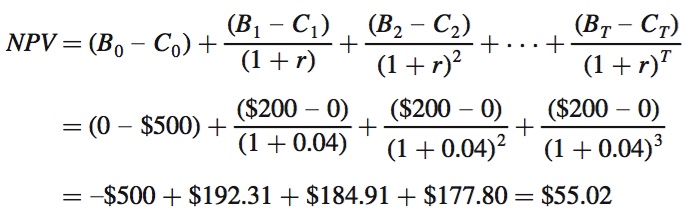
550
The NPV formula is extremely useful and can be used to evaluate all sorts of investment decisions regardless of the timing of their positive or negative payouts.
The Key Role of Interest Rates in Determining NPV
For payment streams with both positive and negative terms, the value of the interest rate r can determine whether the net present value NPV is positive or negative. This is because the interest rate, through its discounting role, determines how important future payoffs are relative to those occurring nearer to the present time period. As r rises, more distant payoffs become relatively less important. Mathematically speaking, this is because the term (1 + r)t in the denominator grows larger with t.
This characteristic means that investment projects tend to become less appealing in NPV terms when the interest rate is higher. Investment projects typically have up-
You can see the economic intuition behind this result if you recognize that the interest rate can be thought of as the opportunity cost of investing. Consider households or firms that are deciding whether to put financial capital toward a potential investment project. They face a choice. They can invest and earn the investment’s returns, or they could instead lend their funds on the financial market to other investors implementing their own projects. A household could do this by holding assets in, say, a mutual fund rather than building an addition to their house. Firms can also use financial markets to offer their uncommitted funds to others. If the firm or household chooses to undertake an investment project, it is giving up the return it could have made by lending to others through the financial market. What is that return? The interest rate r. That’s why r captures the opportunity cost of investing. The higher the market interest rate is, therefore, the more a household or firm gives up by investing. NPV analysis, by putting all payments on a common present-
Application: Replacing Planes
On November 4, 2012, a ribbon-
When deciding whether to purchase the new aircraft, United Airlines’ management team considered two options.4 They could buy the replacement planes at about $250 million each, or they could keep their existing 767-
551
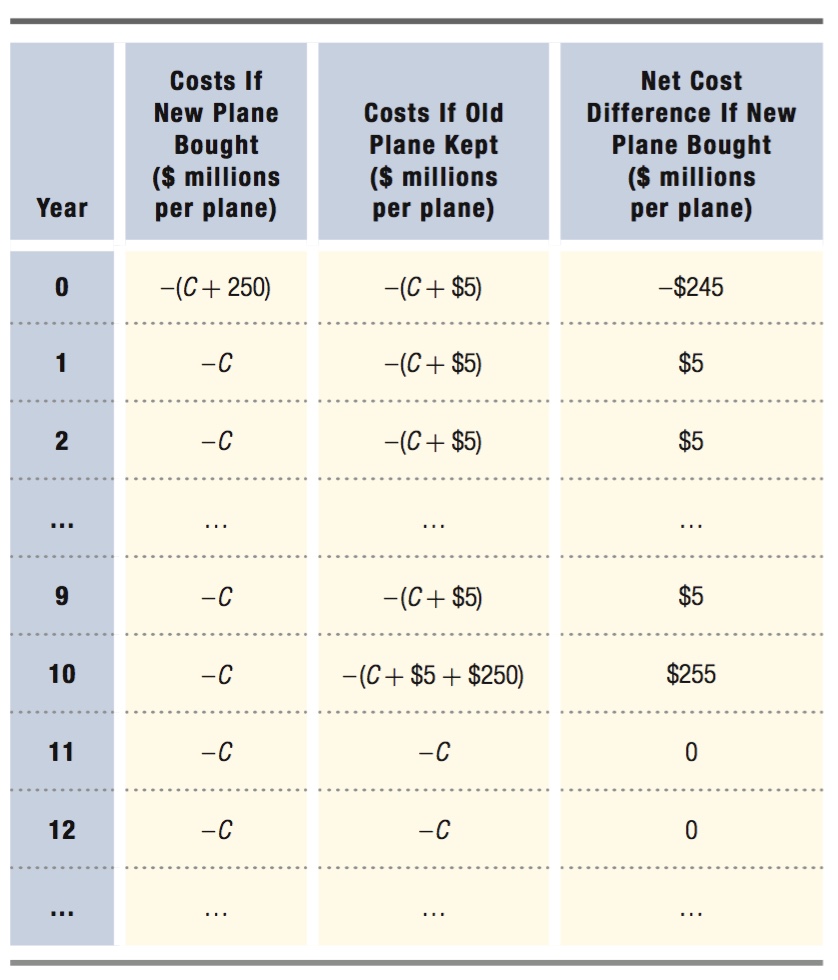
Let’s start the analysis by laying out the payment flows. If United opted to buy new planes, it would have to pay $250 million per plane immediately and operating costs C per year thereafter.
If United did not buy the new planes, it would pay operating costs C plus the additional $880 per hour in fuel costs. Long-
United had to decide which of these cost streams would be smallest. Table 14.2 shows the difference between the two payment streams over the relevant horizon.
552
Looking at the difference in costs makes it clear that buying the new planes is an investment: United pays an up-
Suppose the interest rate United faces is 5%. We first compute the PDV of each year’s net payment as shown in the third column of Table 14.2. These PDVs are given in the first column of Table 14.3. Their sum is the per-
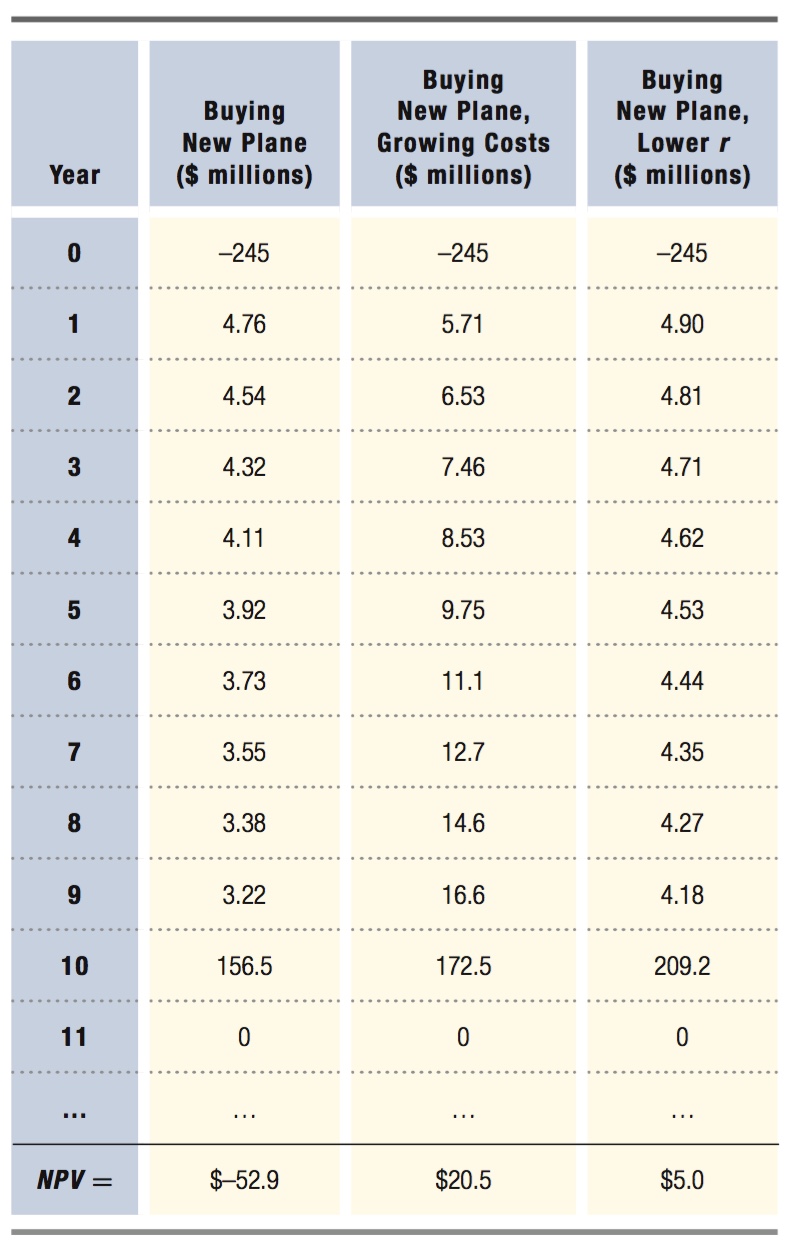
Under what circumstances might United have found it beneficial to replace the 767-
Suppose United anticipates that the additional operating costs of the 767-
As a final case, let’s suppose again that the fuel cost difference is fixed at $5 million per year, but that United faces a lower interest rate of 2%. This lower interest rate means that the future cost savings won’t be discounted as much, nor will the savings from not having to purchase new planes 10 years from now. Both of these factors raise the value of buying the new planes right away, and that’s exactly what we see in Column 3 of Table 14.3. The NPV of purchasing now is $5.0 million per plane.
When United received its first Dreamliner, interest rates were at historical lows, and it was plausible that fuel prices and maintenance costs for the 767-
NPVs versus Payback Periods
payback period
The length of time required for an investment’s initial costs to be recouped in future benefits without discounting future flows.
You’ve probably heard investment evaluations couched in terms of payback periods, the time it takes for an investment’s initial costs to be recouped in undiscounted future benefits. For our ski purchase example above, the payback period is three years. The total benefits obtained after two years ($200 + $200 = $400) are less than the $500 up-
553
Payback periods are extremely easy to compute; that’s the advantage of using them to evaluate investment choices. Their disadvantage is that they don’t take into account the idea of discounting future money by an interest rate. They treat future payments as equivalent to current payments in dollar terms, even though that’s not the case (unless the interest rate is zero). The skis, for example, would be considered worthwhile in payback period terms as long as three years is an acceptable period to the person making a decision about the investment. At high enough interest rates, however, the purchase will have a negative NPV. You would do better by not buying the skis and earning interest on the $500 instead. If you had used the payback period method as an evaluation standard when interest rates are high, you would mistakenly buy the skis. For this reason, while payback periods are a handy “first-
figure it out 14.2
For interactive, step-
Marty owns a travel agency and is considering the purchase of a flux capacitor. Owning the capacitor will enable Marty to earn $100,000 per year selling trips through time. Marty plans to hold on to the capacitor for three years. He estimates that at the end of three years, he will be able to resell the flux capacitor for $250,000.
If the flux capacitor is priced at $475,000 and interest rates are 7%, calculate the net present value of the investment.
Is the flux capacitor a wise investment for Marty? Explain.
Solution:
Net present value is the present value of the benefits minus the present value of the costs for each period. We must account for three factors in this calculation: the price Marty must pay initially, the revenue he earns each of the three periods, and the amount he will receive from selling the capacitor at the end of the three years. Therefore,

Note that the cost of $475,000 is occurring now, so it is not discounted (and it enters the equation with a minus sign), while the benefits (the annual revenue and the sale price) occur in the future and thus must be discounted.
Calculating, we get
NPV = –$475,000 + $93,457.94 + $87,343.87 + $81,629.79 + $204,074.47 = –$8,493.93
No, this is not a wise investment for Marty because the NPV is negative.