Centromeres are not genes, but they are regions of DNA on which the orderly reproduction of living organisms absolutely depends and are therefore of great interest in genetics. In most eukaryotes, recombination analysis cannot be used to map the loci of centromeres because they show no heterozygosity that can enable them to be used as markers. However, in the fungi that produce linear tetrads (see Chapter 3), centromeres can be mapped. We will use the fungus Neurospora as an example. Recall that, in haploid fungi such as Neurospora, haploid nuclei from each parent fuse to form a transient diploid, which undergoes meiotic divisions along the long axis of the ascus, and so each meiocyte produces a linear array of eight ascospores, called an octad. These eight ascospores constitute the four products of meiosis (a tetrad) plus a postmeiotic mitosis.

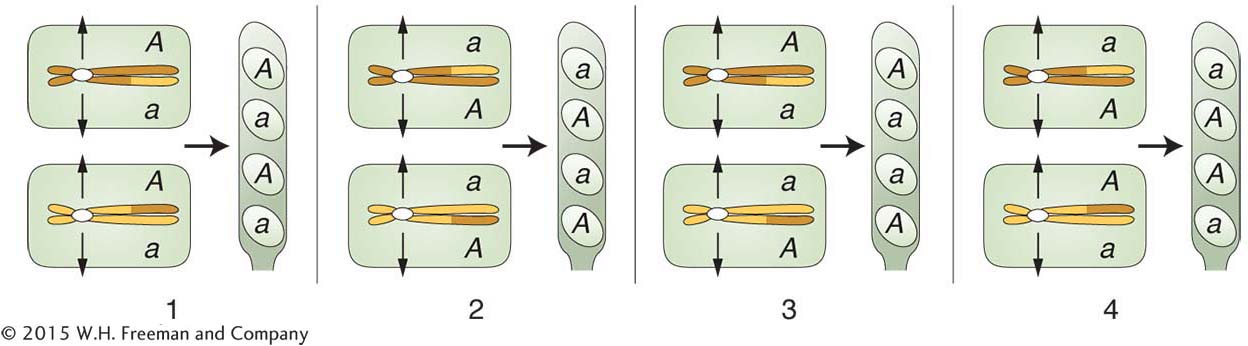
In its simplest form, centromere mapping considers a gene locus and asks how far this locus is from its centromere. The method is based on the fact that a different pattern of alleles will appear in a linear tetrad or octad that arises from a meiosis with a crossover between a gene and its centromere. Consider a cross between two individuals, each having a different allele at a locus (say, A × a). Mendel’s law of equal segregation dictates that, in an octad, there will always be four ascospores of genotype A and four of a, but how will they be arranged? If there has been no crossover in the region between A/a and the centromere, there will be two adjacent blocks of four ascospores in the linear octad (see Figure 3-10). However, if there has been a crossover in that region, there will be one of four different patterns in the octad, each pattern showing blocks of two adjacent identical alleles. Some data from an actual cross of A × a are shown in the following table.

149

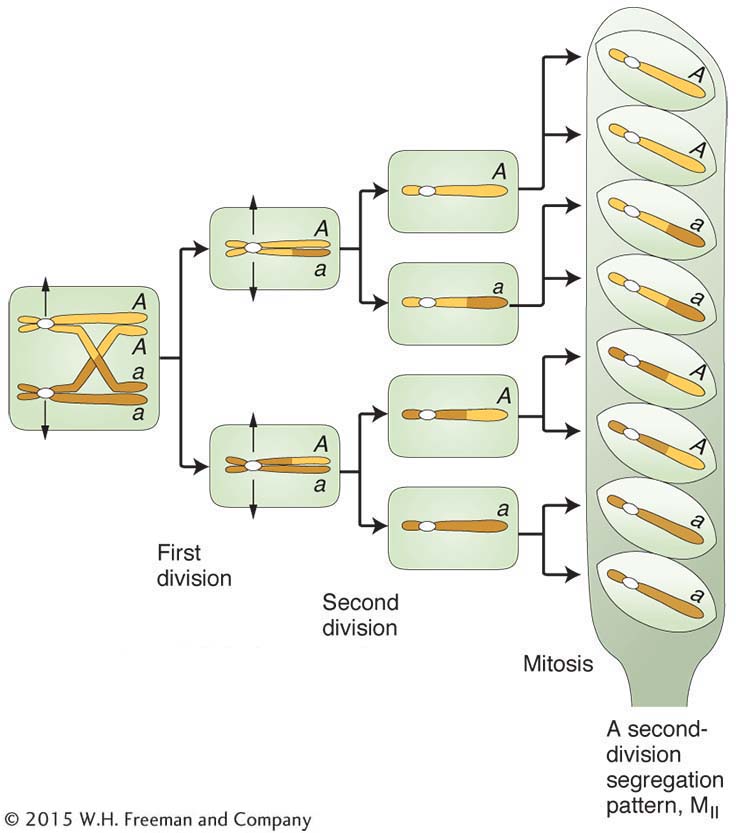
The first two columns on the left are from meioses with no crossover in the region between the A locus and the centromere. The letter M is used to stand for a type of segregation at meiosis. The patterns for the first two columns are called M_I patterns, or first-division segregation patterns, because the two different alleles segregate into the two daughter nuclei at the first division of meiosis. The other four columns are all from meiocytes with a crossover. These patterns are called second-division segregation patterns (M_II) because, as a result of crossing over in the centromere-to-locus region, the A and a alleles are still together in the nuclei at the end of the first division of meiosis (Figure 4-17). There has been no first-division segregation. However, the second meiotic division does segregate the A and a alleles into separate nuclei. The other patterns are produced similarly; the difference is that the chromatids move in different directions at the second division (Figure 4-18).

You can see that the frequency of octads with an M_II pattern should be proportional to the size of the centromere-A/a region and could be used as a measure of the size of that region. In our example, the M_II frequency is 42/300 = 14 percent. Does this percentage mean that the A/a locus is 14 m.u. from the centromere? The answer is no, but this value can be used to calculate the number of map units. The 14 percent value is a percentage of meioses, which is not the way that map units are defined. Map units are defined as the percentage of recombinant chromatids issuing from meiosis. Because a crossover in any meiosis results in only 50 percent recombinant chromatids (four out of eight; see Figure 4-17), we must divide the 14 percent by 2 to convert the M_II frequency (a frequency of meioses) into map units (a frequency of recombinant chromatids). Hence, this region must be 7 m.u. in length, and this measurement can be introduced into the map of that chromosome.

150