PROBLEMS
WORKING WITH THE FIGURES
Question 1
Which individual in Figure 18-3 has the most heterozygous loci, and which individual has the fewest?
Question 2
Suppose that the seven chromosomes in Figure 18-4a represent a random sample of chromosomes from a population.
Calculate gene diversity (GD) separately for the indel, the microsatellite locus, and the SNP at position 3.
If the sequence was shortened so that you had data only for positions 1 through 24, how many haplotypes would there be?
Calculate the linkage disequilibrium parameter (D) between the SNPs at positions 29 and 33.
Question 3
Looking at Figure 18-6, can you count how many mitochondrial haplotypes were carried from Asia into the Americas?
Question 4
In Figure 18-13, the “unrelated” (blue) column for Japan is higher than the “unrelated” column for France. What does this tell you?
Question 5
In Figure 18-14, some individuals have unique SNP alleles—
Question 6
Looking at Figure 18-20, do people of the Middle East tend to have higher or lower levels of heterozygosity compared to the people of East Asia? Why might this be the case?
BASIC PROBLEMS
Question 7
What are the forces that can change the frequency of an allele in a population?
Question 8
What assumptions are made when using the Hardy–
Question 9
In a population of mice, there are two alleles of the A locus (A1 and A2). Tests showed that, in this population, there are 384 mice of genotype A1/A1, 210 of A1/A2, and 260 of A2/A2. What are the frequencies of the two alleles in the population?
Question 10
In a natural population of Drosophila melanogaster, the alcohol dehydrogenase gene has two alleles called F (fast) and S (slow) with frequencies of Adh-
Question 11
In a randomly mating laboratory population of Drosophila, 4 percent of the flies have black bodies (encoded by the autosomal recessive b), and 96 percent have brown bodies (the wild type, encoded by B). If this population is assumed to be in Hardy–
Question 12
In a population of a beetle species, you notice that there is a 3:1 ratio of shiny to dull wing covers. Does this ratio prove that the shiny allele is dominant? (Assume that the two states are caused by two alleles of one gene.) If not, what does it prove? How would you elucidate the situation?
Question 13
Cystic fibrosis (CF) is an autosomal recessive disorder that occurs relatively frequently among people of European descent. In an Amish community in Ohio, medical researchers reported the occurrence of cystic fibrosis (CF) as being 1/569 live births. Using the Hardy–
Question 14
The relative fitness values of three genotypes are wA/A = 1.0, wA/a = 1.0, and wa/a = 0.7
If the population starts at the allele frequency p = 0.5, what is the value of p in the next generation?
What is the predicted equilibrium allele frequency if the rate of mutation of A to a is 2 × 10−5?
Question 15
A/A and A/a individuals are equally fertile. If 0.1 percent of the population is a/a, what selection pressure exists against a/a if the A → a mutation rate is 10−5? Assume that the frequencies of the alleles are at their equilibrium values.
Question 16
When alleles at a locus act in a semidominant fashion on fitness, the relative fitness of the heterozygote is midway between the two homozygous classes. For example, genotypes with semidominance at the A locus might have these relative fitnesses: wA/A = 1.0, wA/a = 0.9, and wa/a = 0.8.
Change one of these fitness values so that a/a becomes a deleterious recessive allele.
Change one of these fitness values so that A/A becomes a favored dominant allele.
Question 17
If the recessive allele for an X-
Question 18
Red-
Question 19
Is a new neutral mutation more likely to reach fixation in a large or small population?
Question 20
It seems clear that inbreeding causes a reduction in fitness. Can you explain why?
Question 21
In a population of 50,000 diploid individuals, what is the probability that a new neutral mutation will ultimately reach fixation? What is the probability that it will ultimately be lost from the population?
Question 22
Inbreeding in a population causes a deviation from Hardy–
Question 23
Sickle-
Question 24
You have a sample of 10 DNA sequences of 100 bp in length from a section of highly conserved gene from 10 individuals of a species. The 10 sequences are almost entirely identical; however, each sequence carries one unique SNP not found in any of the others. What is the nucleotide diversity for this sample of sequences?
CHALLENGING PROBLEMS
Question 25
Figure 18-14 presents haplotype data for the G6PD gene in a worldwide sample of people.
Draw a haplotype network for these haplotypes. Label the branches on which each SNP occurs.
Which of the haplotypes has the most connections to other haplotypes?
On what continents is this haplotype found?
Counting the number of SNPs along the branches of your network, how many differences are there between haplotypes 1 and 12?
Question 26
Figure 18-12 shows a pedigree for the offspring of a half-
If the inbreeding coefficient for the common ancestor (A) in Figure 18-12 is 1/2, what is the inbreeding coefficient of I?
If the inbreeding coefficient of individual I in Figure 18-12 is 1/8, what is the inbreeding coefficient of the common ancestor, A?
Question 27
Consider 10 populations that have the genotype frequencies shown in the following table:
|
Population |
A/A |
A/a |
a/a |
|---|---|---|---|
|
1 |
1.0 |
0.0 |
0.0 |
|
2 |
0.0 |
1.0 |
0.0 |
|
3 |
0.0 |
0.0 |
1.0 |
|
4 |
0.50 |
0.25 |
0.25 |
|
5 |
0.25 |
0.25 |
0.50 |
|
6 |
0.25 |
0.50 |
0.25 |
|
7 |
0.33 |
0.33 |
0.33 |
|
8 |
0.04 |
0.32 |
0.64 |
|
9 |
0.64 |
0.32 |
0.04 |
|
10 |
0.986049 |
0.013902 |
0.000049 |
Which of the populations are in Hardy–
Weinberg equilibrium? What are p and q in each population?
In population 10, the A → a mutation rate is discovered to be 5 × 10 −6. What must be the fitness of the a/a phenotype if the population is at equilibrium?
In population 6, the a allele is deleterious; furthermore, the A allele is incompletely dominant; so A/A is perfectly fit, A/a has a fitness of 0.8, and a/a has a fitness of 0.6. If there is no mutation, what will p and q be in the next generation?
Question 28
The hemoglobin B gene (Hb) has a common allele (A) of a SNP (rs334) that encodes the HbA form of (adult) hemoglobin and a rare allele (T) that encodes the sickling form of hemoglobin, HbS. Among 571 residents of a village in Nigeria, 440 were A/A and 129 were A/T, and 2 were T/T individuals were observed. Use the χ2 test to determine whether these observed genotypic frequencies fit Hardy–
Question 29
A population has the following gametic frequencies at two loci: AB = 0.4, Ab = 0.1, aB = 0.1, and ab = 0.4. If the population is allowed to mate at random until linkage equilibrium is achieved, what will be the expected frequency of individuals that are heterozygous at both loci?
Question 30
Two species of palm trees differ by 50 bp in a 5000-
Question 31
Color blindness in humans is caused by an X-
Question 32
Using pedigree diagrams, calculate the inbreeding coefficient (F) for the offspring of (a) parent-
Question 33
A group of 50 men and 50 women establish a colony on a remote island. After 50 generations of random mating, how frequent would a recessive trait be if it were at a frequency of 1/500 back on the mainland? The population remains the same size over the 50 generations, and the trait has no effect on fitness.
Question 34
Figure 18-22 shows 10 haplotypes from a population before a selective sweep and another 10 haplotypes many generations later after a selective sweep has occurred for this chromosomal region. There are 11 loci defining each haplotype, including one with a red allele that was the target of selection. In the figure, two loci are designated as A and B. These loci each have two alleles: one black and the other gray. Calculate the linkage disequilibrium parameter (D) between A and B, both before and after the selective sweep. What effect has the selective sweep had on the level of linkage disequilibrium?
Question 35
The recombination rate (r) between linked loci A and B is 0.10. In a population, we observe the following haplo-
|
AB |
0.40 |
|
aB |
0.10 |
|
Ab |
0.10 |
|
ab |
0.40 |
What is the level of linkage disequilibrium as measured by D in the present generation?
What will D be in the next generation?
What is the expected frequency of the Ab haplotype in the next generation?
Using a spreadsheet computer software program, make a graph of the decline in D over 10 generations.
Question 36
Allele B is a deleterious autosomal dominant. The frequency of affected individuals is 4.0 × 10−6. The reproductive capacity of these individuals is about 30 percent that of normal individuals. Estimate μ, the rate at which b mutates to its deleterious allele B. Assume that the frequencies of the alleles are at their equilibrium values.
Question 37
What is the equilibrium heterozygosity for a SNP in a population of 50,000 when the mutation rate is 3 × 10 −8?
Question 38
Of 31 children born of father-
Question 39
The B locus has two alleles B and b with frequencies of 0.95 and 0.05, respectively, in a population in the current generation. The genotypic fitnesses at this locus are wB/B = 1.0, wB/b = 1.0, and wb/b = 0.0
What will the frequency of the b allele be in two generations?
What will the frequency of the b allele be in two generations if the fitnesses were wB/B = 1.0, wB/b = 0.0, and wb/b = 0.0?
Explain why there is a difference in the rate of change for the frequency of the b allele under parts (a) and (b) of this problem.
Question 40
The sd gene causes a lethal disease of infancy in humans when homozygous. One in 100,000 newborns die each year of this disease. The mutation rate from Sd to sd is 2 × 10 −4. What must the fitness of the heterozygote be to explain the observed gene frequency in view of the mutation rate? Assign a relative fitness of 1.0 to Sd/Sd homozygotes. Assume that the population is at equilibrium with respect to the frequency of sd.
Question 41
If we define the total selection cost to a population of deleterious recessive genes as the loss of fitness per individual affected (s) multiplied by the frequency of affected individuals (q2), then selection cost = sq2.
Suppose that a population is at equilibrium between mutation and selection for a deleterious recessive allele, where s = 0.5 and μ = 10−5. What is the equilibrium frequency of the allele? What is the selection cost?
Suppose that we start irradiating individual members of the population so that the mutation rate doubles. What is the new equilibrium frequency of the allele? What is the new selection cost?
If we do not change the mutation rate but we lower the selection coefficient to 0.3 instead, what happens to the equilibrium frequency and the selection cost?
Question 42
Balancing selection acts to maintain genetic diversity at a locus since the heterozygous class has a greater fitness than the homozygous classes. Under this form of selection, the allele frequencies in the population approach an equilibrium point somewhere between 0 and 1. Consider a locus with two alleles A and a with frequencies p and q, respectively. The relative genotypic fitnesses are shown below, where s and g are the selective disadvantages of the two homozygous classes.
|
Genotype |
A/A |
A/a |
a/a |
|---|---|---|---|
|
Relative fitness |
1 − s |
1 |
1 − g |
At equilibrium, the mean fitness of the A alleles (wA) will be equal to the mean fitness of the a alleles (wa) (see Box 18-
7). Set the mean fitness of the A alleles (wA) equal to the mean fitness of the a alleles (wa). Solve the resulting equation for the frequency of the A allele. This is the expression for the equilibrium frequency of A ( 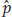 ).
).Using the expression that you just derived, find
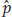 when s = 0.2 and g = 0.8.
when s = 0.2 and g = 0.8.