18.2 The Gene-Pool Concept and the Hardy–Weinberg Law
Perhaps you have watched someone performing a death-
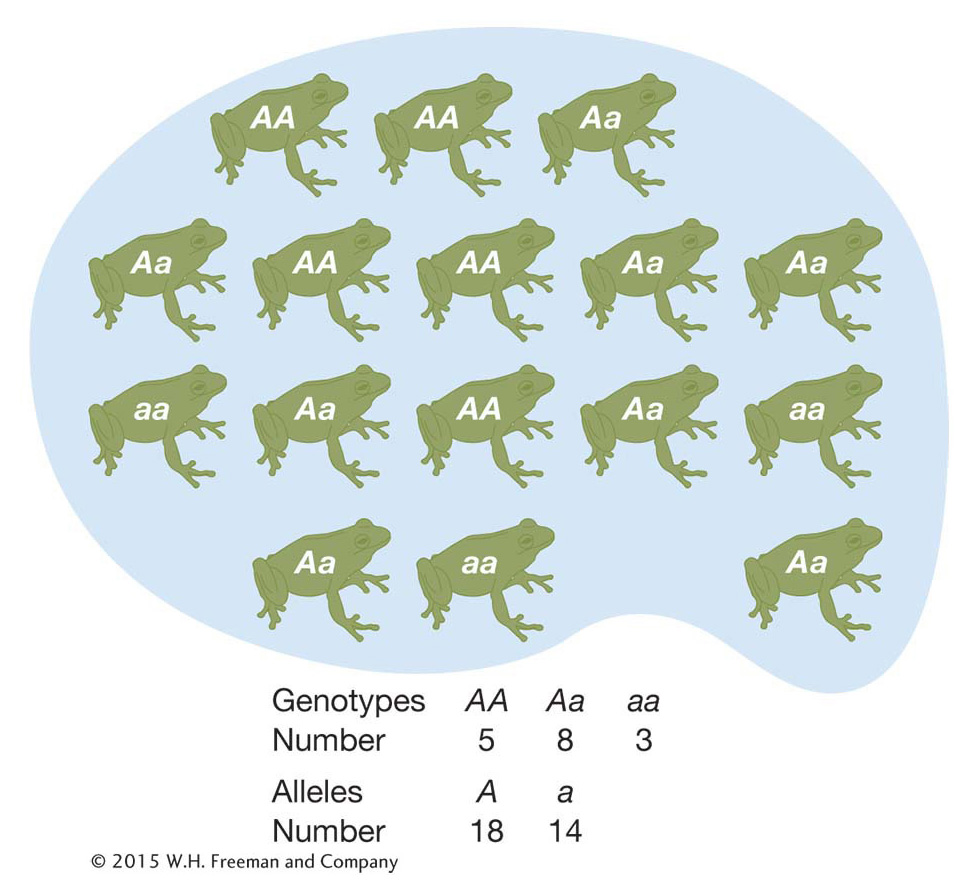
Typically, population geneticists do not care about the absolute counts of the different genotypes in a population but about the genotype frequencies. We can calculate the frequency of the A/A genotype simply by dividing the number of A/A individuals by the total number of individuals in the population (N) to get 0.31. The frequency of A/a heterozygotes is 0.50, and the frequency of a/a homozygotes is 0.19. Since these are frequencies, they sum to 1.0. Frequencies are a more practical measurement than absolute counts because rarely are population geneticists able to study every individual in a population. Rather, population geneticists will draw a random or unbiased sample of individuals from a population and use the sample to infer the genotype frequencies in the entire population.
We can make a simpler description of this frog gene pool if we calculate the allele frequencies rather than the genotype frequencies (Box 18-
BOX 18-1 Calculation of Allele Frequencies
At a locus with two alleles A and a, let’s define the frequencies of the three genotypes A/A, A/a, and a/a as fA/A, fA/a, and fa/a, respectively. We can use these genotype frequencies to calculate the allele frequencies: p is the frequency of the A allele, and q is the frequency of the a allele. Because each homozygote A/A consists only of A alleles and because half the alleles of each heterozygote A/a are A alleles, the total frequency p of A alleles in the population is calculated as
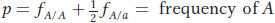
Similarly, the frequency q of the a allele is given by
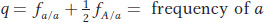
Therefore,
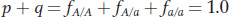
and
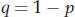
If there are more than two different allelic forms, the frequency for each allele is simply the frequency of its homozygote plus half the sum of the frequencies for all the heterozygotes in which it appears.
KEY CONCEPT
The gene pool is a fundamental concept for the study of genetic variation in populations: it is the sum total of all alleles in the breeding members of a population at a given time. We can describe the variation in a population in terms of genotype and allele frequencies.As mentioned above, an important goal of population genetics is to understand the transmission of alleles from one generation to the next in natural populations. In this section, we will begin to look at how this works. We will see how we can use the allele frequencies in the gene pool to make predictions about the genotype frequencies in the next generation.
The frequency of an allele in the gene pool is equal to the probability that the allele will be chosen when randomly picking an allele from the gene pool to form an egg or a sperm. Knowing this, we can calculate the probability that a frog in the next generation will be an A/A homozygote. If we reach into the frog gene pool (see Figure 18-7) and pick the first allele, the probability that it will be an A is p = 0.56, and similarly the probability that the second allele we pick is also an A is p = 0.56. The product of these two probabilities, or p2 = 0.3136, is the probability that a frog in the next generation will be A/A. The probability that a frog in the next generation will be a/a is q2 = 0.44 × 0.44 = 0.1936. There are two ways to make a heterozygote. We might first pick an A with probability p and then pick an a with probability q, or we might pick the a first and the A second. Thus, the probability that a frog in the next generation will be heterozygous A/a is pq + qp = 2pq = 0.4928. Overall, the frequencies (f) of the genotypes are
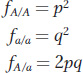
Finally, as expected, the sum of the probability of being A/A plus the probability of being A/a plus the probability of being a/a is 1.0:

This simple equation is the Hardy-Weinberg law, and it is part of the foundation for the theory of population genetics.
The process of reaching into the gene pool to pick an allele is called sampling the gene pool. Since any individual that contributes to the gene can produce many eggs or sperm that carry exactly the same copy of an allele, it is possible to pick a particular copy and then reach back into the gene pool and pick exactly the same copy again. There is also an element of chance involved when sampling the gene pool. Just by chance, some copies may be picked more than once and other copies may not be picked at all. Later in the chapter, we will look at how these properties of sampling the gene pool can lead to changes in the gene pool over time.
We used the Hardy–
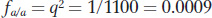
so
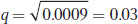
and
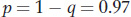
Using the allele frequencies, we can also calculate the frequency of heterozygotes in the population as
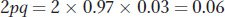
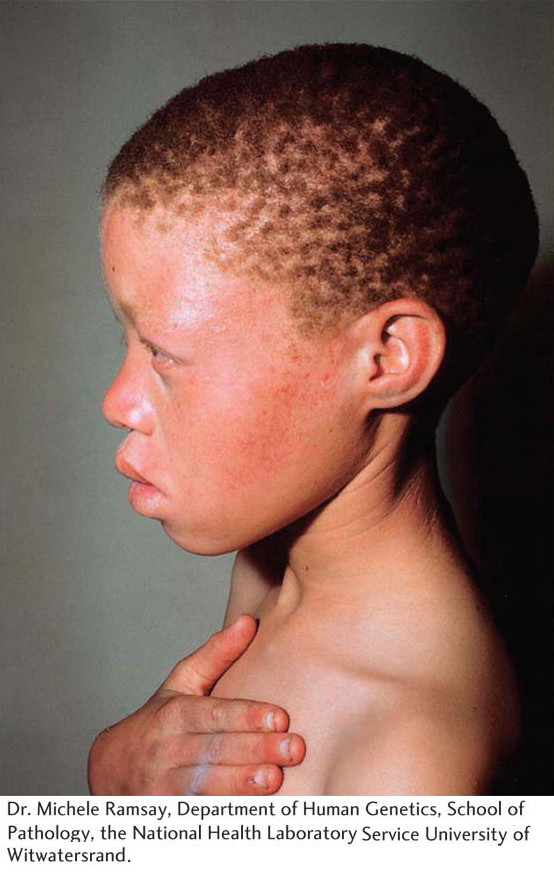
The latter number predicts that about 6 percent of this population are heterozygotes, or carriers of the recessive allele at OCA2.
When we use the Hardy–
First, we assume that mating is random in the population with respect to the gene in question. Deviation from random mating violates this assumption, making it inappropriate to apply Hardy–
Weinberg. For example, a tendency for individuals who are phenotypically similar to mate with each other violates the Hardy– Weinberg law. If albinos mated more frequently with other albinos than with non- albinos, then the Hardy– Weinberg law would overestimate the frequency of the recessive allele. Second, if one of the genotypes has reduced viability such that some individuals with that genotype die before the genotype frequencies are counted, then the estimate of the gene frequencies will be inaccurate.
Third, for the Hardy–
Weinberg law to apply, the population must not be divided into subpopulations that are partially or fully genetically isolated. If there are separate subpopulations, alleles may be present at different frequencies in the different subpopulations. If so, using genotypic counts from the overall population may not give an accurate estimate of the overall allele frequencies. Finally, the Hardy–
Weinberg law strictly applies only to infinitely large populations. For finite populations, there will be deviations from the frequencies predicted by the Hardy– Weinberg law due to chance when sampling the gene pool to produce the next generation.
We have seen how we can use the Hardy–
|
Genotype frequencies |
Gene frequencies |
||||
|---|---|---|---|---|---|
|
Generation |
A/A |
A/a |
a/a |
A |
a |
|
t0 |
0.64 |
0.32 |
0.04 |
0.8 |
0.2 |
|
t1 |
0.64 |
0.32 |
0.04 |
0.8 |
0.2 |
|
⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
|
tn |
0.64 |
0.32 |
0.04 |
0.8 |
0.2 |
Here are a few more points about the Hardy–
1. For any allele that exists at a very low frequency, homozygous individuals will only very rarely be found. If allele a has a frequency of 1 in a thousand (q = 0.001), then only 1 in a million (q2) individuals will be homozygous for that allele. As a consequence, recessive alleles for genetic disorders can occur in the heterozygous state in many more individuals than there are individuals that actually express the genetic disorder in question.
2. The Hardy–
|
Genotype |
Expectation |
Frequency |
|---|---|---|
|
A1A2 |
p21 |
0.25 |
|
A2A2 |
p22 |
0.09 |
|
A3A3 |
p23 |
0.04 |
|
A1A2 |
2p1p2 |
0.30 |
|
A1A3 |
2p1p3 |
0.20 |
|
A2A3 |
2p2p3 |
0.25 |
|
Sum |
1.00 |
3. Hardy–
Male pattern baldness is an X-

4. One can test whether the observed genotype frequencies at a locus fit Hardy–
|
Genotypes |
||||
|---|---|---|---|---|
|
A/A |
A/G |
G/G |
Sum |
|
|
Observed number |
17 |
55 |
12 |
84 |
|
Observed frequency |
0.202 |
0.655 |
0.143 |
1 |
|
Expected frequency |
0.281 |
0.498 |
0.221 |
1 |
|
Expected number |
23.574 |
41.851 |
18.574 |
84 |
|
(Observed − expected)2/expected |
1.833 |
4.131 |
2.327 |
8.29 |
|
Source: International HapMap Project (www.hapmap.org). |
||||
The Hardy–