4.5 4.5 General Probability Rules
When you complete this section, you will be able to:
• Apply the five rules of probability.
• Apply the general addition rule for unions of two or more events.
• Find conditional probabilities.
• Apply the multiplication rule.
• Use a tree diagram to find probabilities.
• Use Bayes’s rule to find probabilities.
• Determine whether or not two events that both have positive probability are independent.
Our study of probability has concentrated on random variables and their distributions. Now we return to the laws that govern any assignment of probabilities. The purpose of learning more laws of probability is to be able to give probability models for more complex random phenomena. We have already met and used five rules.
PROBABILITY RULES
Rule 1. 0 ≤ P(A) ≤ 1 for any event A
Rule 2. P(S) = 1
Rule 3. Addition rule: If A and B are disjoint events, then
P(A or B) = P(A) + P(B)
Rule 4. Complement rule: For any event A,
P(Ac) = 1 − P(A)
Rule 5. Multiplication rule: If A and B are independent events, then
P(A and B) = P(A)P(B)
General addition rules
Probability has the property that if A and B are disjoint events, then P(A or B) = P(A)+P(B). What if there are more than two events or if the events are not disjoint? These circumstances are covered by more general addition rules for probability.
UNION
The union of any collection of events is the event that at least one of the collection occurs.
For two events A and B, the union is the event {A or B} that A or B or both occur. From the addition rule for two disjoint events, we can obtain rules for more general unions. Suppose first that we have several events—say, A, B, and C—that are disjoint in pairs. That is, no two can occur simultaneously. The Venn diagram in Figure 4.15 illustrates three disjoint events. The addition rule for two disjoint events extends to the following law.
ADDITION RULE FOR DISJOINT EVENTS
If events A, B, and C are disjoint in the sense that no two have any outcomes in common, then
P(one or more of A,B,C) = P(A) + P(B) + P(C)
This rule extends to any number of disjoint events.
EXAMPLE 4.40
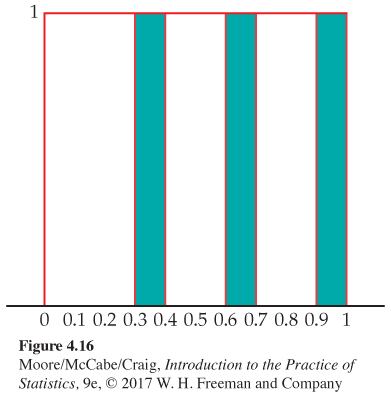
Probabilities as areas. Generate a random number X between 0 and 1. What is the probability that the first digit after the decimal point will be a 3, a 6, or a 9? The random number X is a continuous random variable whose density curve has constant height 1 between 0 and 1 and is 0 elsewhere. The event that the first digit of X is odd is the union of five disjoint events. These events are
0.30 ≤ X < 0.40
0.60 ≤ X < 0.70
0.90 ≤ X < 1.00
Figure 4.16 illustrates the probabilities of these events as areas under the density curve. Each area is 0.1. Therefore, the union of the three has probability equal to the sum, or 0.3.
USE YOUR KNOWLEDGE
Question 4.89
4.89 Probability that you roll a 3 or a 4 or a 5. If you roll a die, the probability of each of the six possible outcomes (1, 2, 3, 4, 5, 6) is 1/6. What is the probability that you roll a 3 or a 4 or a 5?
4.89 P(3 or 4 or 5) = 0.5.
If events A and B are not disjoint, they can occur simultaneously. The probability of their union is then less than the sum of their probabilities. As Figure 4.17 suggests, the outcomes common to both are counted twice when we add probabilities, so we must subtract this probability once. Here is the addition rule for the union of any two events, disjoint or not.
GENERAL ADDITION RULE FOR UNIONS OF TWO EVENTS
For any two events A and B,
P(A or B) = P(A) + P(B) − P(A and B)
If A and B are disjoint, the event {A and B} that both occur has no outcomes in it. This empty event is the complement of the sample space S and must have probability 0. So the general addition rule includes Rule 3, the addition rule for disjoint events.
EXAMPLE 4.41

Adequate sleep and exercise. Suppose that 40% of adults get enough sleep and 46% exercise regularly. What is the probability that an adult gets enough sleep or exercises regularly? To find this probability, we also need to know the percent who get enough sleep and exercise. Let’s assume that 24% do both.
We will use the notation of the general addition rule for unions of two events. Let A be the event that an adult gets enough sleep, and let B be the event that a person exercises regularly. We are given that P(A) = 0.40, P(B) = 0.46, and P(A and B) = 0.24. Therefore,
P(A or B) = P(A) + P(B) − P(A and B)
= 0.40 + 0.46 − 0.24
= 0.62
The probability that an adult gets enough sleep or exercises regularly is 0.62, or 62%.
USE YOUR KNOWLEDGE
Question 4.90
4.90 Probability that your roll is even or greater than 5. If you roll a die, the probability of each of the six possible outcomes (1, 2, 3, 4, 5, 6) is 1/6. What is the probability that your roll is even or greater than 5?
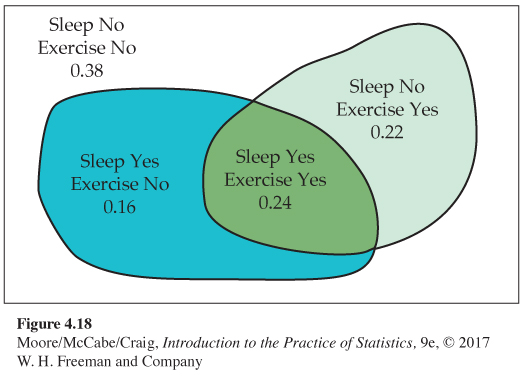
Venn diagrams are a great help in finding probabilities for unions because you can just think of adding and subtracting areas. Figure 4.18 shows some events and their probabilities for Example 4.41. What is the probability that an adult gets adequate sleep and does not exercise?
The Venn diagram shows that the probability that an adult gets adequate sleep minus the probability that an adult gets adequate sleep and exercises regularly is 0.40 − 0.24 = 0.16. Similarly, the probability that an adult does not get adequate sleep and exercises regularly is 0.46 − 0.24 = 0.22. The four probabilities that appear in the figure add to 1 because they refer to four disjoint events whose union is the entire sample space.
Conditional probability
The probability we assign to an event can change if we know that some other event has occurred. This idea is the key to many applications of probability.
EXAMPLE 4.42
Probability of being dealt a heart. Doyle is a professional poker player. He stares at the dealer, who prepares to deal. What is the probability that the card dealt to Doyle is a heart? There are 52 cards in the deck. Because the deck was carefully shuffled, the next card dealt is equally likely to be any of the cards that Doyle has not seen. Thirteen of the 52 cards are hearts. So
P(heart)=1352=14
This calculation assumes that Doyle knows nothing about any cards already dealt. Suppose now that he is looking at four cards already in his hand and that they are all hearts. He knows nothing about the other 48 cards except that exactly nine (13 − 4) hearts are among them. Doyle’s probability of being dealt a heart given what he knows is now
P(heart|4heartsin4visiblecards)=948=316
Knowing that there are four hearts among the four cards Doyle can see changes the probability that the next card dealt is a heart.
The new notation P(A | B) is a conditional probabilityconditional probability. That is, it gives the probability of one event (the next card dealt is a heart) under the condition that we know another event (exactly one of the four visible cards is a heart). You can read the bar | as “given the information that.”
MULTIPLICATION RULE
The probability that both of two events A and B happen together can be found by
P(A and B) = P(A)P(B | A)
Here P(B | A) is the conditional probability that B occurs, given the information that A occurs.
USE YOUR KNOWLEDGE
Question 4.91
4.91 The probability of a heart. Refer to Example 4.42. Suppose that none of the four cards in Doyle’s hand are hearts. What is the probability that the next card dealt to him is a heart?
4.91 13/48 = 0.2708.
EXAMPLE 4.43
Downloading music from the Internet. The multiplication rule is just common sense made formal. For example, suppose that 30% of Internet users download music files, and 70% of downloaders say they don’t care if the music is copyrighted. So the percent of Internet users who download music (event A) and don’t care about copyright (event B) is 70% of the 30% who download, or
(0.7)(0.3) = 0.21 = 21%
The multiplication rule expresses this as
P(A and B) = P(A) × P(B | A)
= (0.3)(0.7) = 0.21
Here is another example that uses conditional probability.
EXAMPLE 4.44
Probability of a favorable draw. Doyle is still at the poker table. At the moment, he has two cards and they are both hearts. He has seen 24 cards and none of other players have any hearts. What is the chance that the next three cards he draws will be hearts? The full deck of 52 cards contains 13 hearts. Therefore, 11 of the unseen cards are hearts. There are 28 (52 − 24) unseen cards. To find Doyle’s probability of drawing three hearts, we first calculate
P(firstcardisaheart)=1128P(secondcardisaheart|firstcardisaheart)=1027P(thirdcardisaheart|firsttwocardsarehearts)=926
Doyle finds both probabilities by counting cards. The probability that the first card drawn is a heart is 11/28 because 11 of the 28 unseen cards are hearts. If the first card is a heart, that leaves 10 hearts among the 27 remaining cards. So the conditional probability of another diamond is 10/27. The multiplication rule now says that
P(next two cards are hearts)=1128×1027=0.146
We again apply the multiplication rule for the third card. The probability that the next three draws are hearts is equal to the probability that the first two draws are hearts times the probability that the third card is a heart given that the first two draws are hearts. This probability is
P(next three cards are hearts)=1128×1027×926=0.050
It is very unlikely that Doyle’s next three cards will be hearts, even though his hearts are the only ones that he has seen.
USE YOUR KNOWLEDGE
Question 4.92
4.92 The probability that the next two cards are hearts. In the setting of Example 4.44, suppose that Doyle’s third card is a heart, so he now has three hearts, and that none of the five additional cards that he sees are hearts What is the probability that the next two cards dealt to Doyle will be hearts?
If P(A) and P(A and B) are given, we can rearrange the multiplication rule to produce a definition of the conditional probability P(B | A) in terms of unconditional probabilities.
DEFINITION OF CONDITIONAL PROBABILITY
When P(A) > 0, the conditional probability of B given A is
P(B|A)=P(AandB)P(A)
![]()
Be sure to keep in mind the distinct roles in P(B | A) of the event B whose probability we are computing and the event A that represents the information we are given. The conditional probability P(B | A) makes no sense if the event A can never occur, so we require that P(A) > 0 whenever we talk about P(B | A).
EXAMPLE 4.45
College students. Here is the distribution of U.S. college students classified by age and full-time or part-time status:
| Age (years) | Full-time | Part-time |
|---|---|---|
| 15 to 19 | 0.21 | 0.02 |
| 20 to 24 | 0.32 | 0.07 |
| 25 to 34 | 0.10 | 0.10 |
| 30 and over | 0.05 | 0.13 |
Let’s compute the probability that a student is aged 20 to 24, given that the student is full-time. We know that the probability that a student is part-time and aged 20 to 24 is 0.32 from the table of probabilities. But what we want here is a conditional probability, given that a student is full-time. Rather than asking about age among all students, we restrict our attention to the subpopulation of students who are full-time. Let
A = the student is between 20 and 24 years of age
B = the student is a full-time student
Our formula is
P(A
We read P(A and B) = 0.32 from the table as we mentioned previously. What about P(B)? This is the probability that a student is full-time. Notice that there are four groups of students in our table that fit this description. To find the probability needed, we add the entries:
P(B) = 0.21 + 0.32 + 0.10 + 0.05 = 0.68
We are now ready to complete the calculation of the conditional probability:
= 0.47
The probability that a student is 20 to 24 years of age, given that the student is full-time, is 0.47.
Here is another way to give the information in the last sentence of this example: 47% of full-time college students are 20 to 24 years old. Which way do you prefer?
USE YOUR KNOWLEDGE
Question 4.93
4.93 What rule did we use? In Example 4.45, we calculated P(B). What rule did we use for this calculation? Explain why this rule applies in this setting.
4.93 The addition rule for disjoint events.
Question 4.94
4.94 Find the conditional probability. Refer to Example 4.45. What is the probability that a student is part-time, given that the student is 20 to 24 years old? Explain in your own words the difference between this calculation and the one that we did in Example 4.45.
General multiplication rules
The definition of conditional probability reminds us that, in principle, all probabilities—including conditional probabilities—can be found from the assignment of probabilities to events that describe random phenomena. More often, however, conditional probabilities are part of the information given to us in a probability model, and the multiplication rule is used to compute P(A and B). This rule extends to more than two events.
The union of a collection of events is the event that any of them occur. Here is the corresponding term for the event that all of them occur.
INTERSECTION
The intersection of any collection of events is the event that all the events occur.
To extend the multiplication rule to the probability that all of several events occur, the key is to condition each event on the occurrence of all the preceding events. For example, the intersection of three events A, B, and C has probability
P(A and B and C) = P(A)P(B | A)P(C | A and B)
EXAMPLE 4.46
High school athletes and professional careers. Only 5% of male high school basketball, baseball, and football players go on to play at the college level. Of these, only 1.7% enter major league professional sports. About 40% of the athletes who compete in college and then reach the pros have a career of more than three years. Define these events:
A = {competes in college}
B = {competes professionally}
C = {pro career longer than 3 years}
What is the probability that a high school athlete competes in college and then goes on to have a pro career of more than three years? We know that
P(A) = 0.05
P(B | A) = 0.017
P(C | A and B) = 0.4
Therefore, the probability we want is
P(A and B and C) = P(A)P(B | A)P(C | A and B)
= 0.05 × 0.017 × 0.4 = 0.00034
Only about 3 of every 10,000 high school athletes can expect to compete in college and have a professional career of more than three years. High school students would be wise to concentrate on studies rather than on unrealistic hopes of fortune from pro sports.
Tree diagrams
Probability problems often require us to combine several of the basic rules into a more elaborate calculation. Here is an example that illustrates how to solve problems that have several stages.
EXAMPLE 4.47
Online chat rooms. Online chat rooms are dominated by the young. Teens are the biggest users. If we look only at adult Internet users (aged 18 and over), 47% of the 18 to 29 age group chat, as do 21% of the 30 to 49 age group and just 7% of those 50 and over. To learn what percent of all Internet users participate in chat, we also need the age breakdown of users. Here it is: 29% of adult Internet users are 18 to 29 years old (event A1), another 47% are 30 to 49 (event A2), and the remaining 24% are 50 and over (event A3).
What is the probability that a randomly chosen adult user of the Internet participates in chat rooms (event C)? To find out, use the tree diagramtree diagram in Figure 4.19 to organize your thinking. Each segment in the tree is one stage of the problem. Each complete branch shows a path through the two stages. The probability written on each segment is the conditional probability of an Internet user following that segment, given that he or she has reached the node from which it branches.
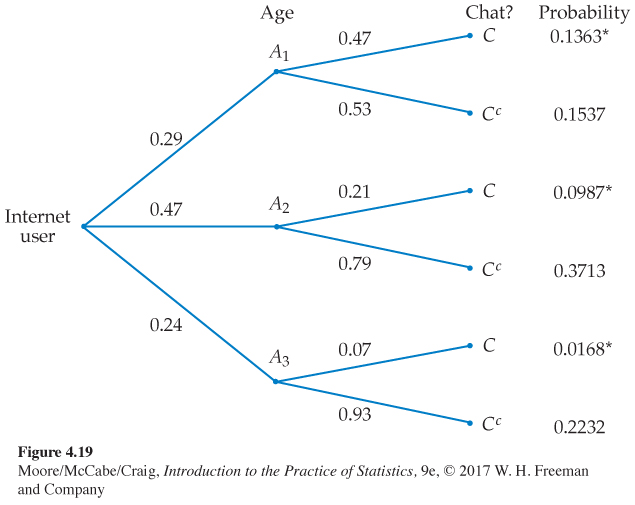
Starting at the left, an Internet user falls into one of the three age groups. The probabilities of these groups
P(A1) = 0.29 P(A2) = 0.47 P(A3) = 0.24
mark the leftmost branches in the tree. Conditional on being 18 to 29 years old, the probability of participating in chat is P(C | A1) = 0.47. So the conditional probability of not participating is
P(Cc | A1) = 1 − 0.47 = 0.53
These conditional probabilities mark the paths branching out from the A1 node in Figure 4.19. The other two age group nodes similarly lead to two branches marked with the conditional probabilities of chatting or not. The probabilities on the branches from any node add to 1 because they cover all possibilities, given that this node was reached.
There are three disjoint paths to C, one for each age group. By the addition rule, P(C) is the sum of their probabilities. The probability of reaching C through the 18 to 29 age group is
P(C and A1) = P(A1)P(C | A1)
= 0.29 × 0.47 = 0.1363
Follow the paths to C through the other two age groups. The probabilities of these paths are
P(C and A2) = P(A2)P(C | A2) = (0.47)(0.21) = 0.0987
P(C and A3) = P(A3)P(C | A3) = (0.24)(0.07) = 0.0168
The final result is
P(C) = 0.1363 + 0.0987 + 0.0168 = 0.2518
About 25% of all adult Internet users take part in chat rooms.
It takes longer to explain a tree diagram than it does to use it. Once you have understood a problem well enough to draw the tree, the rest is easy. Tree diagrams combine the addition and multiplication rules. The multiplication rule says that the probability of reaching the end of any complete branch is the product of the probabilities written on its segments. The probability of any outcome, such as the event C that an adult Internet user takes part in chat rooms, is then found by adding the probabilities of all branches that are part of that event.
USE YOUR KNOWLEDGE
Question 4.95
4.95 Draw a tree diagram. Refer to Doyle’s chances of five hearts in Example 4.44 (page 268). Draw a tree diagram to describe the outcomes for the three cards that he will be dealt. At the first stage, his draw can be a heart or a nonheart. At the second and third stages, he has the same possible outcomes but the probabilities are different.
Bayes’s rule
There is another kind of probability question that we might ask in the context of thinking about online chat. What percent of adult chat room participants are aged 18 to 29?
EXAMPLE 4.48
Conditional versus unconditional probabilities. In the notation of Example 4.47, this is the conditional probability P(A1 | C). Start from the definition of conditional probability and then apply the results of Example 4.47:
More than half of adult chat room participants are between 18 and 29 years old. Compare this conditional probability with the original information (unconditional) that 29% of adult Internet users are between 18 and 29 years old. Knowing that a person chats increases the probability that he or she is young.
We know the probabilities P(A1), P(A2), and P(A3) that give the age distribution of adult Internet users. We also know the conditional probabilities P(C | A1), P(C | A2), and P(C | A3) that a person from each age group chats. Example 4.47 shows how to use this information to calculate P(C). The method can be summarized in a single expression that adds the probabilities of the three paths to C in the tree diagram:
P(C) = P(A1)P(C | A1) + P(A2)P(C | A2) + P(A3)P(C | A3)
In Example 4.48, we calculated the “reverse” conditional probability P(A1 | C). The denominator 0.2518 in that example came from the previous expression. Put in this general notation, we have another probability law.
BAYES’S RULE
Suppose that A1, A2, . . . , Ak are disjoint events whose probabilities are not 0 and add to exactly 1. That is, any outcome is in exactly one of these events. Then if C is any other event whose probability is not 0 or 1,
The numerator in Bayes’s rule is always one of the terms in the sum that makes up the denominator. The rule is named after Thomas Bayes, who wrestled with arguing from outcomes like C back to the Ai in a book published in 1763. It is far better to think your way through problems like Examples 4.47 and 4.48 than to memorize these formal expressions.
Independence again
The conditional probability P(B | A) is generally not equal to the unconditional probability P(B). That is because the occurrence of event A generally gives us some additional information about whether or not event B occurs. If knowing that A occurs gives no additional information about B, then A and B are independent events. The formal definition of independence is expressed in terms of conditional probability.
INDEPENDENT EVENTS
Two events A and B that both have positive probability are independent if
P(B | A) = P(B)
This definition makes precise the informal description of independence given in Section 4.2 (page 229). We now see that the multiplication rule for independent events, P(A and B) = P(A)P(B), is a special case of the general multiplication rule, P(A and B) = P(A)P(B | A), just as the addition rule for disjoint events is a special case of the general addition rule.