9.2 9.2 Goodness of Fit

When you complete this section, you will be able to:

  • • Compute expected counts given a sample size and the probabilities specified by a null hypothesis for a chi-square goodness-of-fit test.

  • • Find the chi-square test statistic and its P-value.

  • • Interpret the results of a chi-square goodness-of-fit significance test.

In the last section, we discussed the use of the chi-square test to compare categorical-variable distributions of c populations. We now consider a slight variation on this scenario where we compare a sample from one population with a hypothesized distribution. Here is an example that illustrates the basic ideas.

EXAMPLE 9.13

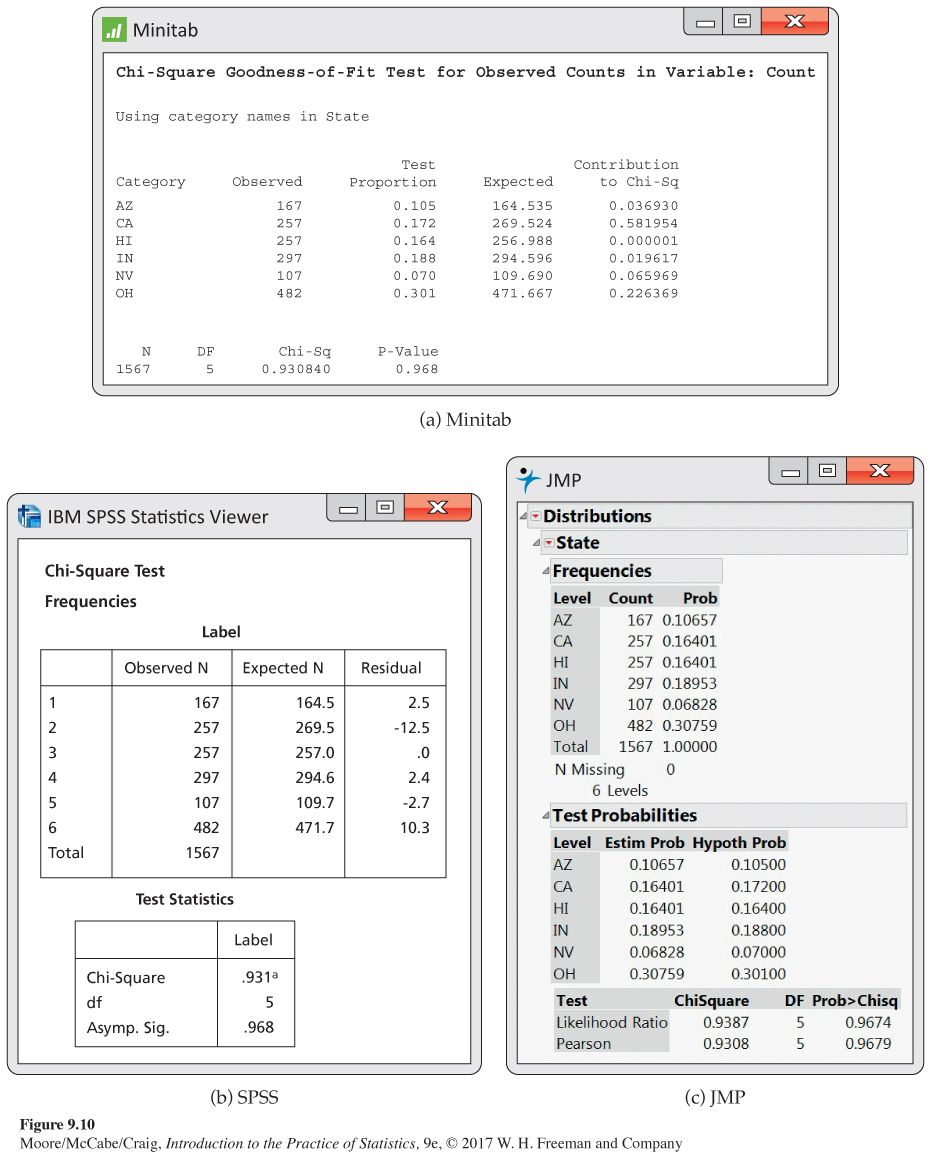
Sampling in the Adequate Calcium Today (ACT) study. The ACT study was designed to examine relationships among bone growth patterns, bone development, and calcium intake. Participants were more than 14,000 adolescents from six states: Arizona (AZ), California (CA), Hawaii (HI), Indiana (IN), Nevada (NV), and Ohio (OH). After the major goals of the study were completed, the investigators decided to do an additional analysis of the written comments made by the participants during the study. Because the number of participants was so large, a sampling plan was devised to select sheets containing the written comments of approximately 10% of the participants. A systematic sample (see page 364) of every 10th comment sheet was retrieved from each storage container for analysis.9 Here are the counts for each of the six states:

546

Number of study participants in the sample
AZ CA HI IN NV OH Total
167 257 257 297 107 482 1567

There were 1567 study participants in the sample. We will use the proportions of students from each of the states in the original sample of more than 14,000 participants as the population values.10 Here are the proportions:

Population proportions
AZ CA HI IN NV OH Total
0.105 0.172 0.164 0.188 0.070 0.301 100.000

Let’s see how well our sample reflects the state population proportions. We start by computing expected counts. Because 10.5% of the population is from Arizona, we expect the sample to have about 10.5% from Arizona. Therefore, because the sample has 1567 subjects, our expected count for Arizona is

Here are the expected counts for all six states:

Expected counts
AZ CA HI IN NV OH Total
164.54 269.52 256.99 294.60 109.69 471.67 1567.01

USE YOUR KNOWLEDGE

Question 9.29

9.29 Why is the sum 1567.01? Refer to the table of expected counts in Example 9.13. Explain why the sum of the expected counts is 1567.01 and not 1567.

Question 9.30

9.30 Calculate the expected counts. Refer to Example 9.13. Find the expected counts for the other five states. Report your results with three places after the decimal as we did for Arizona.

As we saw with the expected counts in the analysis of two-way tables in Section 9.1, we do not really expect the observed counts to be exactly equal to the expected counts. Different samples under the same conditions would give different counts. We expect the average of these counts to be equal to the expected counts when the null hypothesis is true. How close do we think the counts and the expected counts should be?

547

We can think of our table of observed counts in Example 9.13 as a one-way table with six cells, each with a count of the number of subjects sampled from a particular state. Our question of interest is translated into a null hypothesis that says that the observed proportions of students in the six states can be viewed as random samples from the subjects in the ACT study. The alternative hypothesis is that the process generating the observed counts, a form of systematic sampling in this case, does not provide samples that are compatible with this hypothesis. In other words, the alternative hypothesis says that there is some bias in the way we selected the subjects whose comments we will examine.

Our analysis of these data is very similar to the analyses of two-way tables that we studied in Section 9.1. We have already computed the expected counts. We now construct a chi-square statistic that measures how far the observed counts are from the expected counts. Here is a summary of the procedure.

THE CHI-SQUARE GOODNESS-OF-FIT TEST

Data for observations of a categorical variable with possible outcomes are summarized as observed counts, in cells. The null hypothesis specifies probabilities for the possible outcomes. The alternative hypothesis says that the true probabilities of the possible outcomes are not the probabilities specified in the null hypothesis.

For each cell, multiply the total number of observations by the specified probability to determine the expected counts:

The chi-square statistic measures how much the observed cell counts differ from the expected cell counts. The formula for the statistic is

The degrees of freedom are , and -values are computed from the chi-square distribution.

Use this procedure when the expected counts are all 5 or more.

EXAMPLE 9.14

The goodness-of-fit test for the ACT study. For Arizona, the observed count is 167. In Example 9.13, we calculated the expected count, 164.535. The contribution to the chi-square statistic for Arizona is

We use the same approach to find the contributions to the chi-square statistic for the other five states. The expected counts are all at least 5, so we can proceed with the significance test.

The sum of these six values is the chi-square statistic,

548

The degrees of freedom are the number of cells minus 1, . We calculate the -value using Table F or software. From Table F, we can determine . We conclude that the observed counts are compatible with the hypothesized proportions. The data do not provide any evidence that our systematic sample was biased with respect to selection of subjects from different states.

USE YOUR KNOWLEDGE

Question 9.31

9.31 Compute the chi-square statistic. For each of the other five states, compute the contribution to the chi-square statistic using the method illustrated for Arizona in Example 9.14. (You can use the expected counts that you found in Exercise 9.30 for these calculations.) Show that the sum of these values is the chi-square statistic.

EXAMPLE 9.15

The goodness-of-fit test from software. Software output from Minitab, SPSS, and JMP for this problem is given in Figure 9.10. Minitab and SPSS report the -value as 0.968. JMP gives an additional place after the decimal, 0.9679. Note that the SPSS output includes a column titled “Residual.” For tables of counts, a residual for a cell is defined as

that the residual reported by SPSS is the numerator of this ratio. The chi-square statistic is the sum of the squares of these residuals.

Some software packages do not provide routines for computing the chi-square goodness-of-fit test. However, there is a very simple trick that can be used to produce the results from software that can analyze two-way tables. Make a two-way table in which the first column contains cells with the observed counts. Add a second column with counts that correspond exactly to the probabilities specified by the null hypothesis, with a very large number of observations. Then perform the chi-square significance test for two-way tables.

image
Figure 9.10: FIGURE 9.10 (a) Minitab, (b) SPSS, and (c) JMP output, Example 9.15.

549

USE YOUR KNOWLEDGE

Question 9.32

9.32 Distribution of M&M colors. M&M Mars Company has varied the mix of colors for M&M’S Plain Chocolate Candies over the years. These changes in color blends are the result of consumer preference tests. Most recently, the color distribution is reported to be 13% brown, 14% yellow, 13% red, 20% orange, 24% blue, and 16% green.11 You open up a 14-ounce bag of M&M’s and find 61 brown, 59 yellow, 49 red, 77 orange, 141 blue, and 88 green. Use a goodness of fit test to examine how well this bag fits the percents stated by the M&M Mars Company.

EXAMPLE 9.16

The sign test as a goodness-of-fit test. A study of the effect of the full moon on aggressive behaviors of dementia patients included 15 patients, 14 of whom exhibited a greater number of aggressive behaviors on moon days than on other days. The sign test (page 472) tests the null hypothesis that patients are equally likely to exhibit more aggressive behaviors on moon days than on other days. Because the sample proportion is and the null hypothesis is

To look at these data from the viewpoint of goodness of fit, we think of the data as two counts: patients who had a greater number of aggressive behaviors on moon days and patients who had a greater number of aggressive behaviors on other days.

550

Counts
Moon Other Total
14 1 15

If the two outcomes are equally likely, the expected counts are both 7.5 (). The expected counts are both greater than 5, so we can proceed with the significance test.

The test statistic is

We have so the degrees of freedom are 1. From Table F, we conclude that

The sign test can test the null hypothesis versus the one-sided alternative that there was a “moon effect.” Within the framework of the goodness of fit test, we test only the general alternative hypothesis that the distribution of the counts do not follow the specified probabilities. Note that the -value for the sign test versus the one-sided alternative is 0.000488, approximately one-half of the value that we reported from Table F in Example 9.16.