Chapter 9: Inference for Categorical Data

9.1 9.1 Inference for Two-Way Tables

526

When you complete this section, you will be able to:

• Translate a problem from a comparison of two proportions to an analysis of a 2 × 2 table.
• Find the joint distribution, the marginal distributions, and the conditional distributions for a two-way table of counts.
• Identify the joint distribution, the marginal distributions, and the conditional distributions for a two-way table from software output.
• Choose appropriate conditional distributions to describe relationships in a two-way table.
• Compute expected counts from the counts in a two-way table.
• Compute the chi-square statistic, and the P-value from the expected counts in a two-way table. Find the degrees of freedom and use the P-value to draw your conclusion.
• Identify the chi-square statistic, the degrees of freedom, and the P-value for a two-way table from software output. Use the P-value to draw your conclusion.
• For a 2 × 2 table, explain the relationship between the chi-square test and the z test for comparing two proportions.

When we studied inference for two proportions in Chapter 8, we started summarizing the raw data by giving the number of observations in each population (n) and how many of these were classified as “successes” (X ).

EXAMPLE 9.1

Franckreporter/Getty Images

Who uses Instagram? In Example 8.11 (page 507), we compared the proportions of young women and men who use Instagram. The following table summarizes the data used in this comparison:

Population	n	X	= X/n
1 (women)	537	328	0.6108
2 (men)	532	234	0.4398
Total	1069	562	0.5257

These data suggest that the percent of women who use Instagram is 17.1% larger than the percent for men, with a 95% margin of error of 5.9%.

two-way table, p. 136

In this chapter, we consider a different summary of the data. Rather than recording just the count of those who use Instagram, we record counts of all the outcomes in a two-way table.

EXAMPLE 9.2

Two-way table for Instagram users. Here is the two-way table classifying women and men by their Instagram usage:

527

Two-way table for Instagram users
	Sex
User	Male	Female	Total
No	298	209	507
Yes	234	328	562
Total	532	537	1069

We use the term tabler × c table to describe a two-way table of counts with r rows and c columns. The two categorical variables in the table of Example 9.2 are “User” and “Sex.” “User” is the row variable, with values “No” and “Yes,” and “Sex” is the column variable, with values “Male” and “Female.” Because the objective in this example is to compare the sexes, we view “Sex” as an explanatory variable. Just as in Chapter 2 where we used the x-axis for the explanatory variable (page 87), here we use Sex as the column variable. The next example presents another two-way table.

EXAMPLE 9.3

Vaccinations and political party preference. Should parents be able to decide whether or not to vaccinate their children or should all vaccinations be required for all children? A Pew Internet survey asked this question of U.S. adults aged 18 and over.¹ The following table breaks down these results by political party preference:

Observed numbers of adults
	Party
Required	Democratic	Republican	Total
No	230	258	488
Yes	729	479	1208
Total	959	737	1696

The two categorical variables in Example 9.3 are “Required,” with values “No” and “Yes,” and “Party,” with values “Democrat” and “Republican.” We view “Party” as an explanatory variable and “Required” as a categorical response variable.

In Chapter 2, we discussed two-way tables and the basics about joint, marginal, and conditional distributions. We now view those sample distributions as estimates of the corresponding population distributions. Let’s look at some software output that gives these distributions.

EXAMPLE 9.4

Software output for vaccinations and political party. Figure 9.1 shows the output from JMP, Minitab, and SPSS for the vaccination data of Example 9.3. For now, we will just concentrate on the different distributions. Later, we will explore other parts of the output.

The three packages use similar displays for the distributions. In the cells of the table, we find the counts, the conditional distributions of the column variable for each value of the row variable, the conditional distributions of the row variable for each value of the column variable, and the joint distribution. All of these are expressed as percents rather than proportions.

528

Figure 9.1: FIGURE 9.1 Computer output from (a) JMP, (b) Minitab, and (c) SPSS, Examples 9.3 and 9.4.

Let’s look at the entries in the upper-left cell of the JMP output. We see that there are 230 Democrats who think vaccinations should not be required. These 230 represent 13.56% of the study participants. They represent 23.98% of the Democrats in the study. And they represent 47.13% of the respondents who think vaccinations should not be required. The marginal distributions are in the rightmost column and the bottom row. Minitab and SPSS give the same information but not necessarily in the same order.

conditional distributions, p. 140

In Chapter 2, we learned that the key to examining the relationship between two categorical variables is to look at conditional distributions. Let’s do that for the vaccination data.

529

EXAMPLE 9.5

Two-way table of vaccination opinions and political party preference. To compare the frequency of vaccination opinions across political party preference, we examine column percents. Here they are, rounded from the output in Figure 9.1 for clarity:

Column percents for political party
	Party
Required	Democratic	Republican
No	24%	35%
Yes	76%	65%
Total	100%	100%

The “Total” row reminds us that 100% of the Democrats and Republicans have been classified as either thinking that vaccinations should be required or not. (The sums sometimes differ slightly from 100% because of roundoff error.) The bar graphs in Figure 9.2 compare the percents. The difference between the percents of adults who think vaccinations should not be required is reasonably large (24% for Democrats versus 35% percent for Republicans).

530

Figure 9.2: FIGURE 9.2 Bar graph of the percents of adults who believe vaccinations should not be required (no) and who believe that vaccinations should be required (yes), by political party preference, Example 9.5.

531

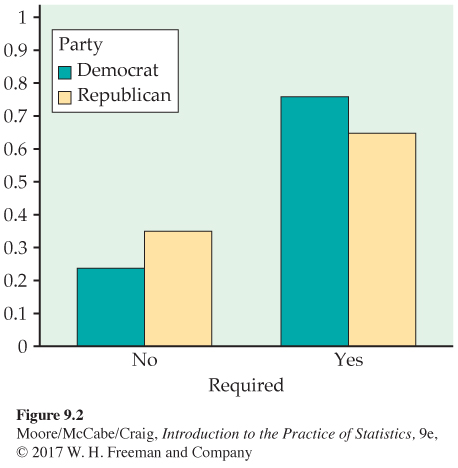
A statistical test will tell us whether or not this difference can be plausibly attributed to chance. Specifically, if there is no association between party preference and opinions about requiring vaccinations, how likely is it that a sample would show a difference as large or larger than that displayed in Figure 9.2? In the last part of this section, we discuss the significance test to examine this question.

Note that Figure 9.2 shows the percents favoring required vaccinations (yes) as well as percents opposed (no). In a description of the results, we would choose one of these for our main story. For tables with more than two columns, we would normally plot the percents for all columns. Here is another way to display the data in a two-way table.

EXAMPLE 9.6

Mosaic plot for vaccination opinions and political party preference. Figure 9.3 displays the joint distribution and the two marginal distributions in a single plot, called a mosaic plot. The sizes of the four rectangles are proportional to the four probabilities of the joint distribution. The bar at the right side gives the marginal distribution of the required variable while the widths of the vertical bars give the marginal distribution of the variable party.

Figure 9.3: FIGURE 9.3 Mosaic plot for the vaccinations and political party data, Example 9.6.

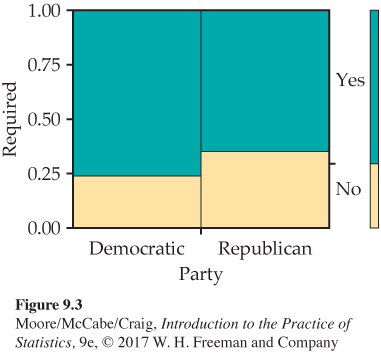
mosaic plot, p. 143

USE YOUR KNOWLEDGE

Question 9.1

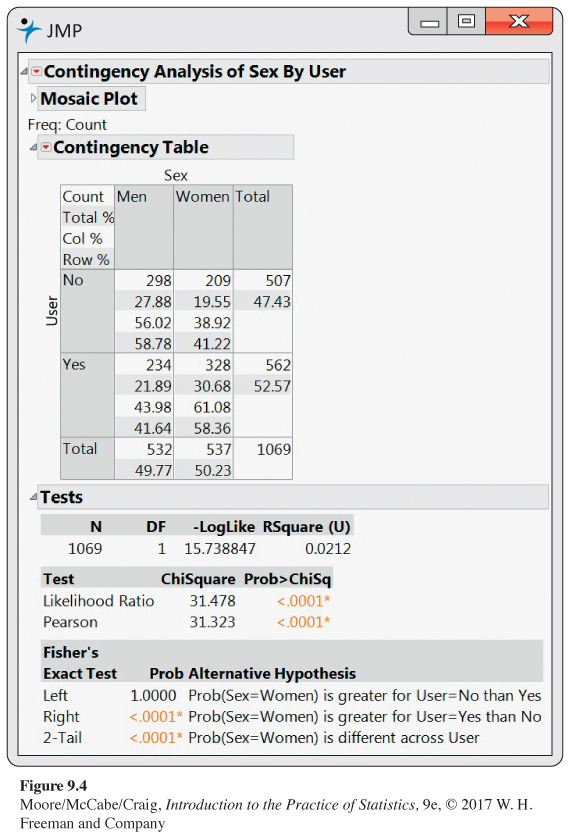
9.1 Find two conditional distributions for the Instagram data. Figure 9.4 shows JMP output for the Instagram data of Example 9.2 (page 526). Use this output to answer the following questions.

(a) Find the conditional distribution of Instagram use for females.
(b) Do the same for males.
(c) Graphically display the two conditional distributions.
(d) Write a short summary interpreting the two conditional distributions.

Question 9.2

9.2 Condition on Instagram user. Refer to the previous exercise. Use the output in Figure 9.4 to answer the following questions.

(a) Find the conditional distribution of sex for Instagram users.
(b) Do the same for those who do not use Instagram.
(c) Graphically display the two conditional distributions.
(d) Write a short summary interpreting the two conditional distributions.

532

Question 9.3

9.3 Which conditional distributions should you use? Refer to your answers to the two previous exercises. Which of these distributions do you prefer for interpreting these data? Give reasons for your answer.

Figure 9.4: FIGURE 9.4 Computer output for Instagram users, Exercises 9.1, 9.2, and 9.3.

The hypothesis: No association

The null hypothesis H₀ of interest in a two-way table is “There is no association between the row variable and the column variable.” In Example 9.3, this null hypothesis says that there is no association between political party preference and belief that vaccinations should be required. The alternative hypothesis is that there is an association between these two variables. The alternative does not specify any particular direction for the association. For two-way tables in general, the alternative includes many different possibilities. Because it includes all sorts of possible associations, we cannot describe as either one-sided or two-sided.

533

In our example, the hypothesis that there is no association between political party preference and opinions about requiring vaccinations is equivalent to the statement that the variables “required” and “party” are independent. For other two-way tables, where the columns correspond to independent samples from c distinct populations, there are c distributions for the row variable, one for each population. The null hypothesis then says that the c distributions of the row variable are identical. The alternative hypothesis is that the distributions are not all the same.

Expected cell counts

To test the null hypothesis in tables, we compare the observed cell counts with expected cell countsexpected cell counts calculated under the assumption that the null hypothesis is true. A numerical summary of the comparison will be our test statistic.

EXAMPLE 9.7

Expected counts from software. The observed and expected counts for the vaccine example appear in the JMP, Minitab, and SPSS computer outputs shown in Figure 9.1 (pages 528–530). The expected counts are given as the last entry in each cell for JMP and Minitab and as the second entry in each cell for SPSS. For example, in the cell for Democrats who do not think that vaccinations should be required, the observed count is 230 and the expected count is 275.939 (JMP) or 275.9 (Minitab and SPSS).

How is this expected count obtained? Look at the percents in the right margin of the tables in Figure 9.1. We see that 28.77% of all adults thought that vaccinations should not be required. If the null hypothesis of no relation between party and required is true, we expect this overall percent to apply to both Democrats and Republicans. In particular, we expect 28.77% of the Democrats to be opposed to making vaccinations required. Because there are 959 Democrats, the expected count is 28.77% of 959, or 275.9. The other expected counts are calculated in the same way.

The reasoning of Example 9.7 leads to a simple formula for calculating expected cell counts. To compute the expected count of Democrats opposed to requiring vaccinations, we multiplied the proportion of adults opposed to requiring vaccinations (488/1696) by the number of Democrats (959). From Figure 9.1, we see that the numbers 488 and 959 are the row and column totals for the cell of interest and that 1696 is n, the total number of observations for the table. The expected cell count is, therefore, the product of the row and column totals divided by the table total.

EXPECTED CELL COUNTS

In Figure 9.3 (page 531), we used a mosaic plot to display the data for the vaccination and political party preference data. Looking at the two columns, we can see that the proportion in the lower region, corresponding to being opposed to required vaccinations, is smaller for the Democrats than for the Republicans. This illustrates graphically the difference in the conditional distributions of required for the two parties. What would the mosaic plot look like if there was no difference? If there was no difference in the conditional distributions, then the two variables would be independent, and the observed counts would be equal to the expected counts. If we rerun the analysis with the expected counts in place of the observed counts, we obtain the mosaic plot in Figure 9.5. Notice that the proportions of each party responding yes are now equal.

534

Figure 9.5: FIGURE 9.5 Mosaic plot for the vaccinations and political party scenario with expected counts in place of observed counts.

The chi-square test

To test the H₀ that there is no association between the row and column classifications, we use a statistic that compares the entire set of observed counts with the set of expected counts. To compute this statistic,

• First, take the difference between each observed count and its corresponding expected count, and square these values so that they are all 0 or positive.
• Because a large difference means less if it comes from a cell that is expected to have a large count, divide each squared difference by the expected count. This is a type of standardization.
• Finally, sum over all cells.

standardizing, p. 59

The result is called the chi-square statistic X². The chi-square statistic was proposed by the English statistician Karl Pearson (1857–1936) in 1900. It is the oldest inference procedure still used in its original form.

CHI-SQUARE STATISTIC

The chi-square statistic is a measure of how much the observed cell counts in a two-way table diverge from the expected cell counts. The formula for the statistic is

where “observed” represents an observed cell count, “expected” represents the expected count for the same cell, and the sum is over all cells in the table.

535

Figure 9.6: FIGURE 9.6 (a) The χ²(2) density curve. (b) The χ²(4) density curve.

If the expected counts and the observed counts are very different, a large value of will result. Large values of provide evidence against the null hypothesis. To obtain a P-value for the test, we need the sampling distribution of under the assumption that (no association between the row and column variables) is true. The distribution is called the chi-square distributionchi-square distribution χ², which we denote by ( is the lowercase Greek letter chi).

Like the distributions, the distributions form a family described by a single parameter, the degrees of freedom. We use to indicate a particular member of this family. Figure 9.6 displays the density curves of the and distributions. As you can see in the figure, distributions take only positive values and are skewed to the right. Table F in the back of the book gives upper critical values for the distributions.

degrees of freedom, p. 409

CHI-SQUARE TEST FOR TWO-WAY TABLES

The null hypothesis is that there is no association between the row and column variables in a two-way table. The alternative hypothesis is that these variables are related.

If is true, the chi-square statistic has approximately a distribution with degrees of freedom.

The P-value for the chi-square test is

where is a random variable having the distribution with . For tables larger than , we will use this approximation whenever the average of the expected counts is 5 or more and the smallest expected count is 1 or more. For tables, we require all four cell counts to be 5 or more.²

The chi-square test always uses the upper tail of the distribution because any deviation from the null hypothesis makes the statistic larger. The approximation of the distribution of by becomes more accurate as the cell counts increase. Moreover, it is more accurate for tables larger than tables.

536

EXAMPLE 9.8

Chi-square significance test from software. The results of the chi-square significance test for the vaccination example appear in the computer outputs in Figure 9.1 (pages 928–930), labeled Pearson (JMP) or Pearson Chi-square (Minitab and SPSS). Because all the expected cell counts are large (5 or more), the distribution provides an accurate -value. We see that , , and Note that Minitab and SPSS report the -value as 0.000 or .000. These are rounded numbers and potentially misleading. The -value is small, but it is not zero. For this reason, we prefer to report As a check, we verify that the degrees of freedom are correct for a table:

The chi-square test confirms that the data provide evidence against the null hypothesis that there is no relationship between political party preference and vaccination opinion. Under , the chance of obtaining a value of greater than or equal to the calculated value of 12.29 is small, less than 0.0001—fewer than 1 time in 10,000.

The outputs in Figure 9.1 also report results for testing the hypothesis of no association using alternatives to the chi-square significance test. Fisher’s exact test is preferred by many, particularly when the counts are small and the chi-square approximation is not very accurate.

The test does not provide insight into the nature of the relationship between the variables. It is up to us to see that the data show that Republicans are more likely to believe that vaccinations should not be required. You should always accompany a chi-square test by percents such as those in Example 9.5 and Figure 9.3 and by a description of the nature of the relationship.

Observational studies such as the one in Example 9.3 cannot tell us whether or not an explanatory variable is a cause of a pattern in a response variable. For the party and vaccine scenario, a causal association does not seem plausible. Often, association can be explained by confounding with other variables.

confounding, p. 150

Computations

The calculations required to analyze a two-way table are straightforward but tedious. In practice, we recommend using software, but it is possible to do the work with a calculator, and some insight can be gained by examining the details. Here is an outline of the steps required.

COMPUTATIONS FOR TWO-WAY TABLES

1. Calculate descriptive statistics that convey the important information in the table. Usually, these will be column or row percents.
2. Find the expected counts and use these to compute the statistic.
3. Use chi-square critical values from Table F to find the approximate -value.
4. Draw a conclusion about the association between the row and column variables.

The next few examples illustrate these steps.

537

EXAMPLE 9.9

Health habits of college students. Physical activity generally declines when students leave high school and enroll in college. This suggests that college is an ideal setting to promote physical activity. One study examined the level of physical activity and other health-related behaviors in a sample of 1184 college students.³ Let’s look at the data for physical activity and consumption of fruits. We categorize physical activity as low, moderate, or vigorous and fruit consumption as low, medium, or high. Here is the two-way table that summarizes the data:

	Physical activity
Fruit consumption	Low	Moderate	Vigorous	Total
Low	69	206	294	569
Medium	25	126	170	321
High	14	111	169	294
Total	108	443	633	1184

The table in Example 9.9 is a 3 × 3 table, to which we have added the marginal totals obtained by summing across rows and columns. For example, the first-row total is 69 + 206 + 294 = 569. The grand total, the number of students in the study, can be computed by summing the row totals (569 + 321 + 294 = 1184), or the column totals (108 + 443 + 633 = 1184). It is easy to make an error in these calculations, so it is a good idea to do both as a check on your arithmetic.

Computing conditional distributions

First, we summarize the observed relation between physical activity and fruit consumption. We expect a positive association, but there is no clear distinction between an explanatory variable and a response variable in this setting. If we have such a distinction, then the clearest way to describe the relationship is to compare the conditional distributions of the response variable for each value of the explanatory variable. Otherwise, we can compute the conditional distribution each way and then decide which gives a better description of the data.

EXAMPLE 9.10

Health habits of college students: Conditional distributions. Let’s look at the data in the first column of the table in Example 9.9. There were 108 students with low physical activity. Of these, there were 69 with low fruit consumption. Therefore, the column proportion for this cell is

That is, 63.9% of the low physical activity students had low fruit consumption. Similarly, 25 of the low physical activity students has moderate fruit consumption. This percent is 23.1%.

538

In all, we calculate nine percents. Here are the results:

Column percents for fruit consumption and physical activity
	Physical activity
Fruit consumption	Low	Moderate	Vigorous	Total
Low	63.9	46.5	46.4	48.1
Medium	23.1	28.4	26.9	27.1
High	13.0	25.1	26.7	24.8
Total	100.0	100.0	100.0	100.0

In addition to the conditional distributions of fruit consumption for each level of physical activity, the table also gives the marginal distribution of fruit consumption. These percents appear in the rightmost column, labeled “Total.”

The sum of the percents in each column should be 100, except for possible small roundoff errors. It is good practice to calculate each percent separately and then sum each column as a check. In this way, we can find arithmetic errors that would not be uncovered if, for example, we calculated the column percent for the “High” row by subtracting the sum of the percents for “Low” and “Medium” from 100.

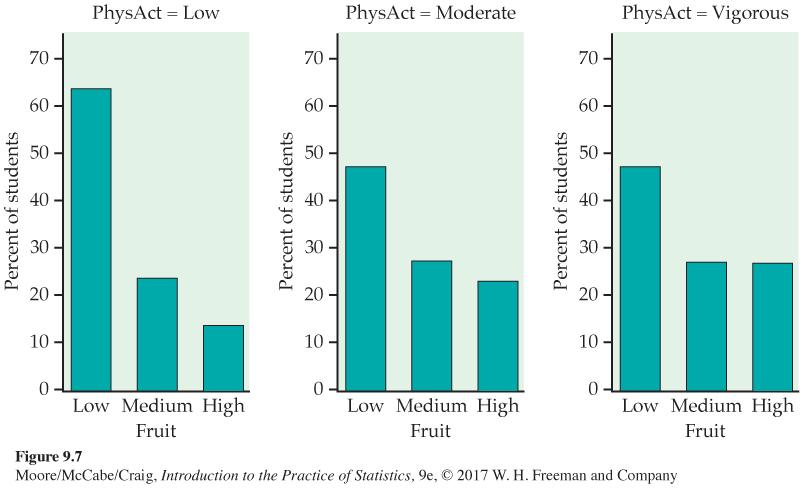
Figure 9.7 compares the distributions of fruit consumption for each of the three physical activity levels. For each activity level, the highest percent is for students who consume low amounts of fruit. For low physical activity, there is a clear decrease in the percent when moving from low to medium to high fruit consumption. The patterns for moderate physical activity and vigorous physical activity are similar. Low fruit consumption is still dominant, but the percents for medium and high fruit consumption are about the same for the moderate and vigorous activity levels. The percent of low fruit consumption is highest for the low physical activity students compared with those who have moderate or vigorous physical activity. These plots suggest that there is an association between these two variables.

Figure 9.7: FIGURE 9.7 Comparison of the distribution of fruit consumption for different levels of physical activity, Example 9.10.

539

USE YOUR KNOWLEDGE

Question 9.4

9.4 Examine the row percents. Refer to the health habits data that we examined in Example 9.9 (page 537). For the row percents, make a table similar to the one in Example 9.10 (page 537).

Question 9.5

9.5 Make some plots. Refer to the previous exercise. Make plots of the row percents similar to those in Figure 9.7.

Question 9.6

9.6 Compare the conditional distributions. Compare the plots you made in the previous exercise with those given in Figure 9.7. Which set of plots do you think gives a better graphical summary of the relationship between these two categorical variables? Give reasons for your answer. Note that there is not a clear right or wrong answer for this exercise. You need to make a choice and to explain your reasons for making it.

We observe a clear relationship between physical activity and fruit consumption in this study. The chi-square test assesses whether this observed association is statistically significant, that is, too strong to occur often just by chance. The test confirms only that there is some relationship. The percents we have compared describe the nature of the relationship.

The chi-square test does not in itself tell us what population our conclusion describes. The subjects in this study were college students from four midwestern universities. The researchers could argue that these findings apply to college students in general. This type of inference is important, but it is based on expert judgment and is beyond the scope of the statistical inference that we have been studying.

EXAMPLE 9.11

The chi-square significance test for health habits of college students. The first step in performing the significance test is to calculate the expected cell counts. Let’s start with the cell for students with low fruit consumption and low physical activity. Using the formula on page 533, we need three quantities: (1) the corresponding row total, 569, the number of students who have low fruit consumption; (2) the column total, 108, the number of students who have low physical activity; and (3) the total number of students, 1184. The expected cell count is, therefore,

Note that although any observed count of the number of students must be a whole number, an expected count need not be.

Calculations for the other eight cells in the table are performed in the same way. With these nine expected counts, we are now ready to use the formula for the statistic on page 534. The first term in the sum comes from the cell for students with low fruit consumption and low physical activity. The observed count is 69 and the expected count is 51.90. Therefore, the contribution to the statistic for this cell is

540

When we add the terms for each of the nine cells, the result is

Because there are levels of fruit consumption and levels of physical activity, the degrees of freedom for this statistic are

Under the null hypothesis that fruit consumption and physical activity are independent, the test statistic has a distribution. To obtain the P-value, look at the df = 4 row in Table F.

df = 4
p	0.01	0.005
	13.28	14.86

The calculated value lies between the critical points for probabilities 0.01 and 0.005. The P-value is, therefore, between 0.01 and 0.005. (Software gives the value as 0.0068.) There is strong evidence (, , ) that there is a relationship between fruit consumption and physical activity.

We can check our work by adding the expected counts to obtain the row and column totals, as in the table. These totals are the same as those in the table of observed counts except for small roundoff errors.

USE YOUR KNOWLEDGE

Question 9.7

9.7 Find the expected counts. Refer to Example 9.11. Compute the expected counts and display them in a table. Check your work by adding the expected counts to obtain row and column totals. These should be the same as those in the table of observed counts except for small roundoff errors.

Question 9.8

9.8 Find the statistic. Refer to the previous exercise. Use the formula on page 534 to compute the contributions to the chi-square statistic for each cell in the table. Verify that their sum is 14.15.

Question 9.9

9.9 Find the -value. For each of the following give the degrees of freedom and an appropriate bound on the -value for the statistic.

(a) for a table.
(b) for a table.
(c) for a table.
(d) for a table.

Question 9.10

9.10 Instagram users: The chi-square test. Refer to Example 9.2 (page 526). Use the chi-square test to assess the relationship between sex and Instagram use. State your conclusion.

The chi-square test and the z test

A comparison of the proportions of “successes” in two populations leads to a table. We can compare two population proportions either by the chi-square test or by the two-sample test from Section 8.2. In fact, these tests always give exactly the same result because the statistic is equal to the square of the statistic and critical values are equal to the squares of the corresponding critical values. The advantage of the test is that we can test either one-sided or two-sided alternatives. The chi-square test always tests the two-sided alternative. Of course, the chi-square test can compare more than two populations, whereas the test compares only two.

541

USE YOUR KNOWLEDGE

Question 9.11

9.11 Comparison of conditional distributions. Consider the following table.

Observed counts
	Explanatory variable
Response variable	1	2	Total
Yes	75	95	170
No	135	115	250
Total	210	210	420

(a) Compute the conditional distribution of the response variable for each of the two explanatory-variable categories.
(b) Display the distributions graphically.
(c) Write a short paragraph describing the two distributions and how they differ.

Question 9.12

9.12 Expected cell counts and the chi-square test. Refer to Exercise 9.11. You consider using the chi-square test to compare these two conditional distributions.

(a) Find the expected counts for all cells. Are they large enough to justify use of the chi-square test for these data?
(b) Computer software gives you X²= 3.95. What are the degrees of freedom for this statistic?
(c) Using Table F, give an appropriate bound on the P-value.

Question 9.13

9.13 Compare the chi-square test with the z test. Refer to the previous two exercises and the significance test for comparing two proportions (page 512).

(a) Set up the problem as a comparison between two proportions. Describe the population proportions, state the null and alternative hypotheses, and give the sample proportions.
(b) Carry out the significance test to compare the two proportions. Report the z statistic, the P-value, and your conclusion.
(c) Compare the P-value for this significance test with the one that you reported in the previous exercise.
(d) Verify that the square of the z statistic is the X² statistic given in the previous exercise.

542

BEYOND THE BASICS

Meta-Analysis

Policymakers wanting to make decisions based on research are sometimes faced with the problem of summarizing the results of many studies. These studies may show effects of different magnitudes, some highly significant and some not significant. What overall conclusion can we draw? Meta-analysismeta-analysis is a collection of statistical techniques designed to combine information from different but similar studies. Each individual study must be examined with care to ensure that its design and data quality are adequate. The basic idea is to compute a measure of the effect of interest for each study. These are then combined, usually by taking some sort of weighted average, to produce a summary measure for all of the studies. Of course, a confidence interval for the summary is included in the results. Here is an example.

EXAMPLE 9.12

Do we eat too much salt? Evidence from a variety of sources suggests that diets high in salt are associated with risks to human health. To investigate the relationship between salt intake and stroke, information from 14 studies was combined in a meta-analysis.⁴ Subjects were classified based on the amount of salt in their normal diet. They were followed for several years and then classified according to whether or not they had developed cardiovascular disease (CVD). A total of 104,933 subjects were studied, and 5161 of them developed CVD. Here are the data from one of the studies:⁵

	Low salt	High salt
CVD	88	112
No CVD	1081	1134
Total	1169	1246

relative risk, p. 518

Let’s look at the relative risk for this study. We first find the proportion of subjects who developed CVD in each group. For the subjects with a low salt intake, the proportion who developed CVD is

or 75 per thousand; for the high-salt group, the proportion is

or 90 per thousand. We can now compute the relative risk as the ratio of these two proportions. We choose to put the high-salt group in the numerator. The relative risk is

Relative risk greater than 1 means that the high-salt group developed more CVD than the low-salt group. For this study, the association is not statistically significant.

543

When the data from all 14 studies were combined, the relative risk was reported as 1.17 with a 95% confidence interval of (1.02, 1.32). Because this interval does not include the value 1, corresponding to equal proportions in the two groups, we conclude that the higher CVD rates are not the same for the two diets (). The high-salt diet is associated with a 17% higher rate of CVD than the low-salt diet. Note that the relative risk for the individual study in this example was not statistically significant, even though it was higher than the overall estimate (1.19 versus 1.17). This illustrates the value of the meta analysis where the conclusion is based on combining results from several studies.

USE YOUR KNOWLEDGE

Question 9.14

9.14 A different view of the relative risk. In the previous example, we computed the relative risk for the high-salt group relative to the low-salt group. Now, compute the relative risk for the low-salt group relative to the high-salt group by inverting the relative risk reported in the meta-analysis in Example 9.15—that is, compute 1/1.17. Then restate the last paragraph of the exercise with this change. (Hint: For the lower confidence limit, use 1 divided by the upper limit for the original ratio and do a similar calculation for the upper limit.)