Budgets and Optimal Consumption
The principle of diminishing marginal utility explains why most people eventually reach a limit, even at an all-
What do we mean by cost? As always, the fundamental measure of cost is opportunity cost. Because the amount of money a consumer can spend is limited, a decision to consume more of one good is also a decision to consume less of some other good.
Budget Constraints and Budget Lines
Consider Sammy, whose appetite is exclusively for clams and potatoes. (There’s no accounting for tastes.) He has a weekly income of $20 and since, given his appetite, more of either good is better than less, he spends all of it on clams and potatoes. We will assume that clams cost $4 per pound and potatoes cost $2 per pound. What are his possible choices?
Whatever Sammy chooses, we know that the cost of his consumption bundle cannot exceed the amount of money he has to spend. That is,
(51-
A budget constraint limits the cost of a consumer’s consumption bundle to no more than the consumer’s income.
A consumer’s consumption possibilities is the set of all consumption bundles that are affordable, given the consumer’s income and prevailing prices.
Consumers always have limited income, which constrains how much they can consume. So the requirement illustrated by Equation 51-
Figure 51.2 shows Sammy’s consumption possibilities. The quantity of clams in his consumption bundle is measured on the horizontal axis and the quantity of potatoes on the vertical axis. The downward-
| Figure 51.2 | The Budget Line |
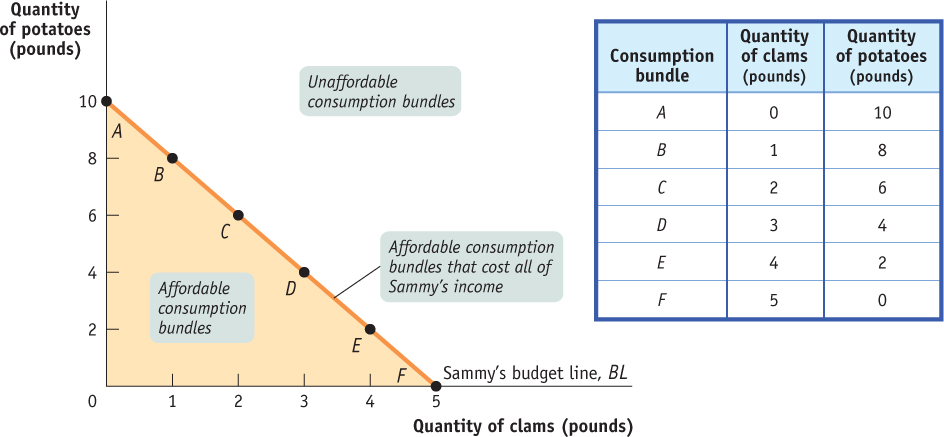
A consumer’s budget line shows the consumption bundles available to a consumer who spends all of his or her income.
The downward-
Do we need to consider the other bundles in Sammy’s consumption possibilities—
Given that $20 per week budget, next we can consider the culinary dilemma of what point on his budget line Sammy will choose.
The Optimal Consumption Bundle
A consumer’s optimal consumption bundle is the consumption bundle that maximizes the consumer’s total utility given his or her budget constraint.
Because Sammy’s budget constrains him to a consumption bundle somewhere along the budget line, a choice to consume a given quantity of clams also determines his potato consumption, and vice versa. We want to find the consumption bundle—
Table 51.1 shows hypothetical levels of utility Sammy gets from consuming various quantities of clams and potatoes, respectively. According to the table, Sammy has a healthy appetite; the more of either good he consumes, the higher his utility. But because he has a limited budget, he must make a trade-
Table 51.1Sammy’s Utility from Clam and Potato Consumption
| Utility from clam consumption | Utility from potato consumption | ||
| Quantity of clams (pounds) | Utility from clams (utils) | Quantity of potatoes (pounds) | Utility from potatoes (utils) |
| 0 | 0 | 0 | 0 |
| 1 | 15 | 1 | 11.5 |
| 2 | 25 | 2 | 21.4 |
| 3 | 31 | 3 | 29.8 |
| 4 | 34 | 4 | 36.8 |
| 5 | 36 | 5 | 42.5 |
| 6 | 47.0 | ||
| 7 | 50.5 | ||
| 8 | 53.2 | ||
| 9 | 55.2 | ||
| 10 | 56.7 | ||
Table 51.2 shows how his total utility varies for the different consumption bundles along his budget line. Each of six possible consumption bundles, A through F from Figure 51.2, is given in the first column. The second column shows the level of clam consumption corresponding to each choice. The third column shows the utility Sammy gets from consuming those clams. The fourth column shows the quantity of potatoes Sammy can afford given the level of clam consumption; this quantity goes down as his clam consumption goes up because he is sliding down the budget line. The fifth column shows the utility he gets from consuming those potatoes. And the final column shows his total utility. In this example, Sammy’s total utility is the sum of the utility he gets from clams and the utility he gets from potatoes.
Table 51.2Sammy’s Budget and Total Utility
| Consumption bundle | Quantity of clams (pounds) | Utility from clams (utils) | Quantity of potatoes (pounds) | Utility from potatoes (utils) | Total utility (utils) |
| A | 0 | 0 | 10 | 56.7 | 56.7 |
| B | 1 | 15 | 8 | 53.2 | 68.2 |
| C | 2 | 25 | 6 | 47.0 | 72.0 |
| D | 3 | 31 | 4 | 36.8 | 67.8 |
| E | 4 | 34 | 2 | 21.4 | 55.4 |
| F | 5 | 36 | 0 | 0 | 36.0 |
Figure 51.3 gives a visual representation of the data shown in Table 51.2. Panel (a) shows Sammy’s budget line, to remind us that when he decides to consume more clams he is also deciding to consume fewer potatoes. Panel (b) then shows how his total utility depends on that choice. The horizontal axis in panel (b) has two sets of labels: it shows both the quantity of clams, increasing from left to right, and the quantity of potatoes, increasing from right to left. The reason we can use the same axis to represent consumption of both goods is, of course, that he is constrained by the budget line: the more pounds of clams Sammy consumes, the fewer pounds of potatoes he can afford, and vice versa.
| Figure 51.3 | Optimal Consumption Bundle |

Clearly, the consumption bundle that makes the best of the trade-
As always, we can find the top of the curve by direct observation. We can see from Figure 51.3 that Sammy’s total utility is maximized at point C—that his optimal consumption bundle contains 2 pounds of clams and 6 pounds of potatoes. But we know that we usually gain more insight into “how much” problems when we use marginal analysis. So in the next section we turn to representing and solving the optimal consumption choice problem with marginal analysis.