As we’ve just seen, we can find Sammy’s optimal consumption choice by finding the total utility he receives from each consumption bundle on his budget line and then choosing the bundle at which total utility is maximized. But we can use marginal analysis instead, turning Sammy’s problem of finding his optimal consumption choice into a “how much” problem. How do we do this? By thinking about choosing an optimal consumption bundle as a problem of how much to spend on each good. That is, to find the optimal consumption bundle with marginal analysis we ask the question of whether Sammy can make himself better off by spending a little bit more of his income on clams and less on potatoes, or by doing the opposite—spending a little bit more on potatoes and less on clams. In other words, the marginal decision is a question of how to spend the marginal dollar—how to allocate an additional dollar between clams and potatoes in a way that maximizes utility.

Our first step in applying marginal analysis is to ask if Sammy is made better off by spending an additional dollar on either good; and if so, by how much is he better off. To answer this question we must calculate the marginal utility per dollar spent on either clams or potatoes—how much additional utility Sammy gets from spending an additional dollar on either good.

We’ve already introduced the concept of marginal utility, the additional utility a consumer gets from consuming one more unit of a good or service; now let’s see how this concept can be used to derive the related measure of marginal utility per dollar.

Table 51.3 shows how to calculate the marginal utility per dollar spent on clams and potatoes, respectively.

522

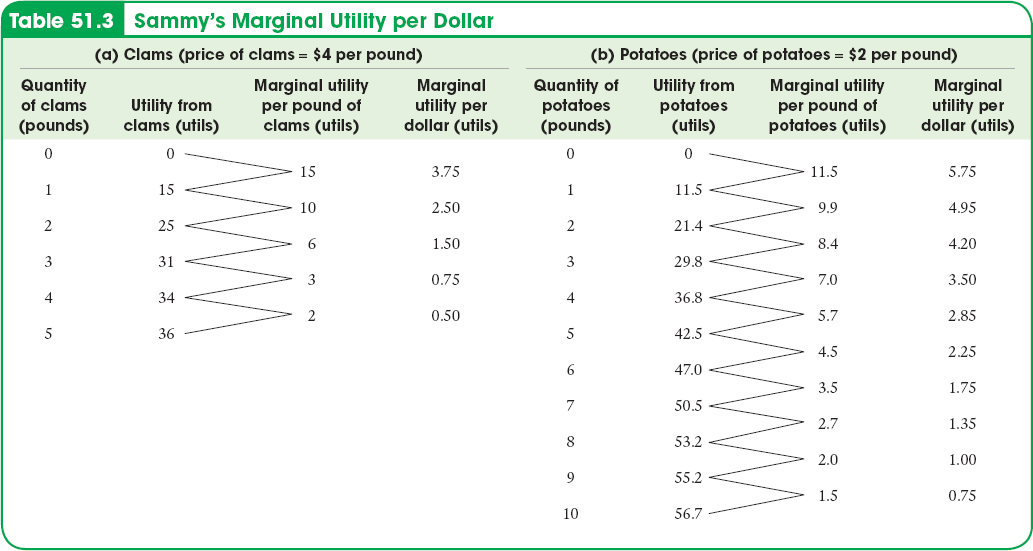
In panel (a) of the table, the first column shows different possible amounts of clam consumption. The second column shows the utility Sammy derives from each amount of clam consumption; the third column then shows the marginal utility, the increase in utility Sammy gets from consuming an additional pound of clams. Panel (b) provides the same information for potatoes. The next step is to derive marginal utility per dollar for each good. To do this, we just divide the marginal utility of the good by its price in dollars.

To see why we divide by the price, compare the third and fourth columns of panel (a). Consider what happens if Sammy increases his clam consumption from 2 pounds to 3 pounds. This raises his total utility by 6 utils. But he must spend $4 for that additional pound, so the increase in his utility per additional dollar spent on clams is 6 utils/$4 = 1.5 utils per dollar. Similarly, if he increases his clam consumption from 3 pounds to 4 pounds, his marginal utility is 3 utils but his marginal utility per dollar is 3 utils/$4 = 0.75 utils per dollar. Notice that because of diminishing marginal utility, Sammy’s marginal utility per pound of clams falls as the quantity of clams he consumes rises. As a result, his marginal utility per dollar spent on clams also falls as the quantity of clams he consumes rises.

So the last column of panel (a) shows how Sammy’s marginal utility per dollar spent on clams depends on the quantity of clams he consumes. Similarly, the last column of panel (b) shows how his marginal utility per dollar spent on potatoes depends on the quantity of potatoes he consumes. Again, marginal utility per dollar spent on each good declines as the quantity of that good consumed rises because of diminishing marginal utility.

We will use the symbols MU_C and MU_P to represent the marginal utility per pound of clams and potatoes, respectively. And we will use the symbols P_C and P_P to represent the price of clams (per pound) and the price of potatoes (per pound), respectively. Then the marginal utility per dollar spent on clams is MU_C/P_C and the marginal utility per dollar spent on potatoes is MU_P/P_P. In general, the additional utility generated from an additional dollar spent on a good is equal to:

(51-2) Marginal utility per dollar spent on a good = Marginal utility of one unit of the good/Price of one unit of the good = MU_good/P_good

Next we’ll see how this concept helps us determine a consumer’s optimal consumption bundle using marginal analysis.

Let’s consider Figure 51.4. As in Figure 51.3, we can measure both the quantity of clams and the quantity of potatoes on the horizontal axis due to the budget constraint. Along the horizontal axis of Figure 51.4—also as in Figure 51.3—the quantity of clams increases as you move from left to right, and the quantity of potatoes increases as you move from right to left. The curve labeled MU_C/P_C in Figure 51.4 shows Sammy’s marginal utility per dollar spent on clams as derived in Table 51.3. Likewise, the curve labeled MU_P/P_P shows his marginal utility per dollar spent on potatoes. Notice that the two curves, MU_C/P_C and MU_P/P_P, cross at the optimal consumption bundle, point C, consisting of 2 pounds of clams and 6 pounds of potatoes. Moreover, Figure 51.4 illustrates an important feature of Sammy’s optimal consumption bundle: when Sammy consumes 2 pounds of clams and 6 pounds of potatoes, his marginal utility per dollar spent is the same, 2, for both goods. That is, at the optimal consumption bundle, MU_C/P_C = MU_P/P_P = 2.

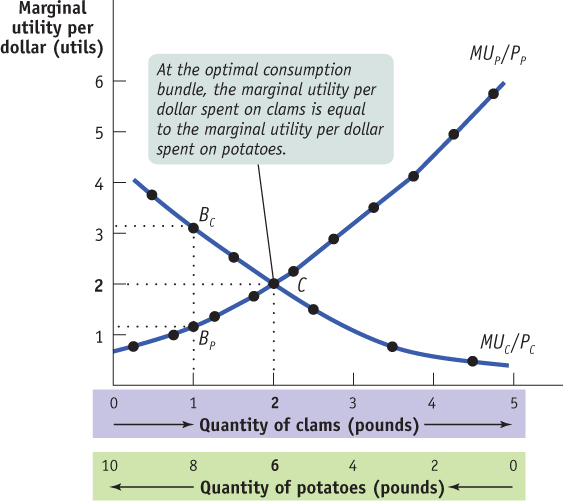
This isn’t an accident. Consider another one of Sammy’s possible consumption bundles—say, B in Figure 51.3, at which he consumes 1 pound of clams and 8 pounds of potatoes. The marginal utility per dollar spent on each good is shown by points B_C and B_P in Figure 51.4. At that consumption bundle, Sammy’s marginal utility per dollar spent on clams would be approximately 3, but his marginal utility per dollar spent on potatoes would be only approximately 1. This shows that he has made a mistake: he is consuming too many potatoes and not enough clams.

523

How do we know this? If Sammy’s marginal utility per dollar spent on clams is higher than his marginal utility per dollar spent on potatoes, he has a simple way to make himself better off while staying within his budget: spend $1 less on potatoes and $1 more on clams. By spending an additional dollar on clams, he adds about 3 utils to his total utility; meanwhile, by spending $1 less on potatoes, he subtracts only about 1 util from his total utility. Because his marginal utility per dollar spent is higher for clams than for potatoes, reallocating his spending toward clams and away from potatoes would increase his total utility. On the other hand, if his marginal utility per dollar spent on potatoes is higher, he can increase his utility by spending less on clams and more on potatoes. So if Sammy has in fact chosen his optimal consumption bundle, his marginal utility per dollar spent on clams and potatoes must be equal.

This is a general principle, known as the optimal consumption rule: when a consumer maximizes utility in the face of a budget constraint, the marginal utility per dollar spent on each good or service in the consumption bundle is the same. That is, for any two goods C and P, the optimal consumption rule says that at the optimal consumption bundle

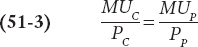
It’s easiest to understand this rule using examples in which the consumption bundle contains only two goods, but it applies no matter how many goods or services a consumer buys: the marginal utilities per dollar spent for each and every good or service in the optimal consumption bundle are equal.

The main reason for studying consumer behavior is to look behind the market demand curve. In Module 46 we explained how the substitution effect leads consumers to buy less of a good when its price increases. We used the substitution effect to explain, in general, why the individual demand curve obeys the law of demand. Marginal analysis adds clarity to the utility-maximizing behavior of individuals and explains more precisely how an increase in price leads to less marginal utility per dollar and therefore a decrease in the quantity demanded.