MODULE 78: Income Inequality and Income Distribution

Economic Inequality

The United States is a rich country. In 2012, the average U.S. household had an income of more than $71,000, far exceeding the poverty threshold. How is it possible, then, that so many Americans still live in poverty? The answer is that income is unequally distributed, with many households earning much less than the average and others earning much more.

Table 78.2 shows the distribution of pre-tax income among U.S. families in 2012—income before federal income taxes are paid—as estimated by the Census Bureau. Households are grouped into quintiles, each containing 20% or one-fifth of the population. The first, or bottom, quintile contains households whose income put them below the 20th percentile in income, the second quintile contains households whose income put them between the 20th and 40th percentiles, and so on. The Census Bureau also provides data on the 5% of families with the highest incomes.

Table 78.2U.S. Income Distribution in 2012

Income group	Income range	Average income	Percent of total income
Bottom quintile	Less than $20,599	$11,490	3.2%
Second quintile	$20,599 to $39,764	29,696	8.3
Third quintile	$39,764 to $64,582	51,179	14.4
Fourth quintile	$64,582 to $104,096	82,098	23.0
Top quintile	More than $104,096	181,905	51.0
Top 5%	More than $191,156	318,052	22.3
Mean Income = $71,274		Median Income = $51,017
Source: U.S. Census Bureau.

Table 78.2: Table 78.2 U.S. Income Distribution in 2012

774

For each group, Table 78.2 shows three numbers. The second column shows the range of incomes that define the group. For example, in 2012, the bottom quintile consisted of households with annual incomes of less than $20,599; the next quintile of households with incomes between $20,599 and $39,764; and so on. The third column shows the average income in each group, ranging from $11,490 for the bottom fifth to $318,052 for the top 5 percent. The fourth column shows the percentage of total U.S. income received by each group.

Mean household income is the average income across all households.

Median household income is the income of the household lying in the middle of the income distribution.

At the bottom of Table 78.2 are two useful numbers for thinking about the incomes of American households. Mean household income, also called average household income, is the total income of all U.S. households divided by the number of households. Median household income is the income of a household in the exact middle of the income distribution—the level of income at which half of all households have lower income and half have higher income. It’s very important to realize that these two numbers do not measure the same thing. Economists often illustrate the difference by asking people first to imagine a room containing several dozen more or less ordinary wage-earners and then to think about what happens to the mean and median incomes of the people in the room if a billionaire Wall Street tycoon walks in. The mean income soars, because the tycoon’s income pulls up the average, but median income hardly rises at all. This example helps explain why economists generally regard median income as a better guide to the economic status of typical American families than mean income: mean income is strongly affected by the incomes of a relatively small number of very-high-income Americans, who are not representative of the population as a whole; median income is not.

AP® Exam Tip

The Course Description published for AP^® Economics teachers by the College Board recommends coverage of the Lorenz curve and the Gini coefficient. Although you will not need to calculate the Gini coefficient, you may need to interpret Gini coefficient values for the AP^® exam.

What we learn from Table 78.2 is that income in the United States is quite unequally distributed. The average income of the poorest fifth of families is less than a quarter of the average income of families in the middle, and the richest fifth have an average income more than three times that of families in the middle. On average, the incomes of the richest fifth of the population are about 15 times as high as those of the poorest fifth. In fact, the distribution of income in America has become more unequal since 1980, rising to a level that has made it a significant political issue. The FYI at the end of this section discusses long-term trends in U.S. income inequality, which declined in the 1930s and 1940s, was stable for more than 30 years after World War II, but began rising again in the late 1970s.

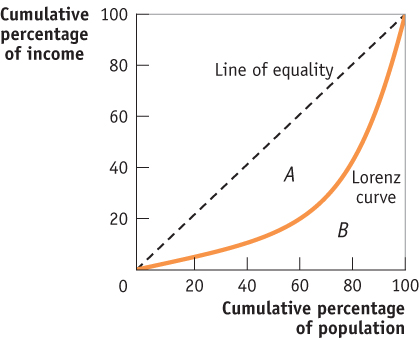
The Lorenz curve shows the percentage of all income received by the poorest members of the population, from the poorest 0% to the poorest 100%.

We can visualize income inequality with the Lorenz curve as shown in Figure 78.2. The Lorenz curve indicates the percentage of all income received by the poorest members of the population, starting from the poorest 0% who receive 0% of the income and ending with the poorest 100% who receive 100% of the income. If income were equally distributed—that is, if the poorest 20% of the population received 20% of the income, the poorest 40% of the population received 40% of the income, and so on—the Lorenz curve would coincide with the line of equality. However, from the data in Table 78.2, we know, for example, that the poorest 20% receive 3.2% of the income and the poorest 40% receive 3.2% + 8.4% = 11.6% percent of the income, so the Lorenz curve falls below the line of equality.

Figure 78.2: The Lorenz CurveThe Lorenz curve indicates the percentage of all income received by the poorest members of the population, starting from the poorest 0% who receive 0% of the income and ending with the poorest 100% who receive 100% of the income. If everyone received the same income, the Lorenz curve would follow the line of equality. Income inequality causes the Lorenz curve to fall below the line of equality.

The Gini coefficient is a number that summarizes a country’s level of income inequality based on how unequally income is distributed.

775

It’s often convenient to have a single number that summarizes a country’s level of income inequality. The Gini coefficient, the most widely used measure of inequality, is the ratio of area A in Figure 78.2, between the line of equality and the Lorenz curve, to area B, below the line of equality. So we have

Gini coefficient = A/(A + B)

A country with a perfectly equal distribution of income would have a Gini coefficient of 0, because the Lorenz curve would follow the line of equality, and area A would be zero. At the other extreme, the highest possible value for the Gini coefficient is 1—the level it would attain if all of a country’s income went to just one person. In that case, area A would equal area A + B, because the Lorenz curve would lie along the horizontal axis until the richest person was included, at which point it would jump up to a height of 100%.

One way to get a sense of what Gini coefficients mean in practice is to look at international comparisons. Figure 78.3 shows the most recent estimates of the Gini coefficient for many of the world’s countries. Aside from a few countries in Africa, the highest levels of income inequality are found in Latin America; countries with a high degree of inequality, such as Brazil, have Gini coefficients close to 0.6. The most equal distributions of income are in Europe, especially in Scandinavia; countries with very equal income distributions, such as Sweden, have Gini coefficients around 0.25. Compared to other wealthy countries, the United States, with a Gini coefficient of 0.477 in 2012, has unusually high inequality, though it isn’t as unequal as in Latin America.

Figure 78.3: Income Inequality Around the WorldThe highest levels of income inequality are found in Africa and Latin America. The most equal distributions of income are in Europe, especially in Scandinavia. Compared to other wealthy countries, the United States, with a Gini coefficient of 0.477 in 2012, has unusually high inequality.

Sources: World Bank, CIA World Factbook, various years depending on data availability.

776

Long-Term Trends in Income Inequality in the United States

Does inequality tend to rise, fall, or stay the same over time? The answer is yes—all three. Over the course of the past century, the United States has gone through periods characterized by all three trends: an era of falling inequality during the 1930s and 1940s, an era of stable inequality for about 35 years after World War II, and an era of rising inequality over the past generation.

Detailed U.S. data on income by quintiles, as shown in Table 78.2, are only available starting in 1947. The figure shows the annual rate of growth of income, adjusted for inflation, for each quintile over two periods: from 1947 to 1980, and from 1980 to 2012. There’s a clear difference between the two periods. In the first period, income within each group grew at about the same rate—that is, there wasn’t much change in the inequality of income, just growing incomes across the board. After 1980, however, incomes grew much more quickly at the top than in the middle, and more quickly in the middle than at the bottom. So inequality has increased substantially since 1980. Overall, inflation-adjusted income for the top quintile rose 48% between 1980 and 2012, but it rose only 0.5% for the bottom quintile.

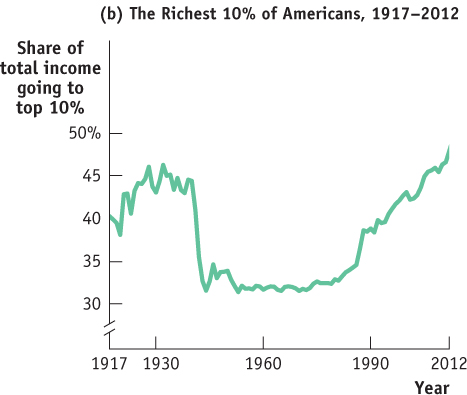
Although detailed data on income distribution aren’t available before 1947, economists have instead used other information including income tax data to estimate the share of income going to the top 10% of the population all the way back to 1917. Panel (b) of the figure shows this measure from 1917 to 2012. These data, like the more detailed data available since 1947, show that American inequality was more or less stable between 1947 and the late 1970s but has risen substantially since. The longer-term data also show, however, that the relatively equal distribution of 1947 was something new. In the late nineteenth century, often referred to as the Gilded Age, American income was very unequally distributed; this high level of inequality persisted into the 1930s. But inequality declined sharply between the late 1930s and the end of World War II. In a famous paper, Claudia Goldin and Robert Margo, two economic historians, dubbed this narrowing of income inequality “the Great Compression.”

The Great Compression roughly coincided with World War II, a period during which the U.S. government imposed special controls on wages and prices. Evidence indicates that these controls were applied in ways that reduced inequality—for example, it was much easier for employers to get approval to increase the wages of their lowest-paid employees than to increase executive salaries. What remains puzzling is that the equality imposed by wartime controls lasted for decades after those controls were lifted in 1946.

Since the 1970s, as we’ve already seen, inequality has increased substantially. In fact, pre-tax income appears to be as unequally distributed in America today as it was in the 1920s, prompting many commentators to describe the current state of the nation as a new Gilded Age—albeit one in which the effects of inequality are moderated by taxes and the existence of the welfare state. There is intense debate among economists about the causes of this widening inequality. The most popular explanation is rapid technological change, which has increased the demand for highly skilled or talented workers more rapidly than the demand for other workers, leading to a rise in the wage gap between the highly skilled and other workers. Growing international trade may also have contributed by allowing the United States to import labor-intensive products from low-wage countries rather than making them domestically, reducing the demand for less skilled American workers and depressing their wages. Rising immigration may be yet another source. On average, immigrants have lower education levels than native-born workers and increase the supply of low-skilled labor while depressing low-skilled wages.

All of these explanations, however, fail to account for one key feature: much of the rise in inequality doesn’t reflect a rising gap between highly educated workers and those with less education, but rather growing differences among highly educated workers themselves. For example, schoolteachers and top business executives have similarly high levels of education, but executive paychecks have risen dramatically and teachers’ salaries have not. For some reason, the economy now pays a few “superstars”—a group that includes literal superstars in the entertainment world but also such groups as Wall Street traders and top corporate executives—much higher incomes than it did a generation ago. It’s still not entirely clear what caused the change.

Source: census.gov

Source: “Income Inequality in the United States, 1913–1998” with Thomas Piketty. Tables and FIGUREs updated in 2012.

777

How serious an issue is income inequality? In a direct sense, high income inequality means that some people don’t share in a nation’s overall prosperity. As we’ve seen, rising inequality explains how it’s possible that the U.S. poverty rate has failed to fall for the past 35 years even though the country as a whole has become considerably richer. Also, extreme inequality, as found in Latin America, is often associated with political instability, because of tension between a wealthy minority and the rest of the population.

It’s important to realize, however, that the data shown in Table 78.2 overstate the true degree of inequality in America, for several reasons. One is that the data represent a snapshot for a single year, whereas the incomes of many individual families fluctuate over time. That is, many of those near the bottom in any given year are having an unusually bad year and many of those at the top are having an unusually good one. Over time, their incomes will revert to a more normal level. So a table showing average incomes within quintiles over a longer period, such as a decade, would not show as much inequality. Furthermore, a family’s income tends to vary over its life cycle: most people earn considerably less in their early working years than they will later in life, and then experience a considerable drop in income when they retire. Consequently, the numbers in Table 78.2, which combine young workers, mature workers, and retirees, show more inequality than would a table that compares families of similar ages.

Despite these qualifications, there is a considerable amount of genuine inequality in the United States. Moreover, the fact that families’ incomes fluctuate from year to year isn’t entirely good news. Measures of inequality in a given year do overstate true inequality. But those year-to-year fluctuations are part of a problem that worries even affluent families—economic insecurity.