Graphs That Depict Numerical Information
Graphs can also be used as a convenient way to summarize and display data without assuming some underlying causal relationship. Graphs that simply display numerical information are called numerical graphs. Here we will consider four types of numerical graphs: time-
Source: Statistics Canada.
Types of Numerical Graphs
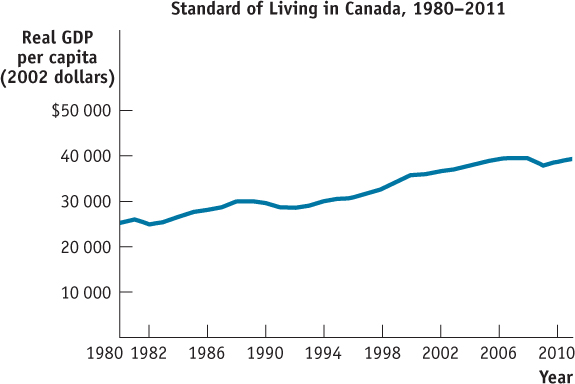
A time-series graph has dates on the horizontal axis and values of a variable that occurred on those dates on the vertical axis.
You have probably seen graphs in newspapers that show what has happened over time to economic variables such as the unemployment rate or stock prices. A time-series graph has successive dates on the horizontal axis and the values of a variable that occurred on those dates on the vertical axis. For example, Figure 2A-8 shows real gross domestic product (GDP) per capita—
Source: OECD Factbook, 2012.
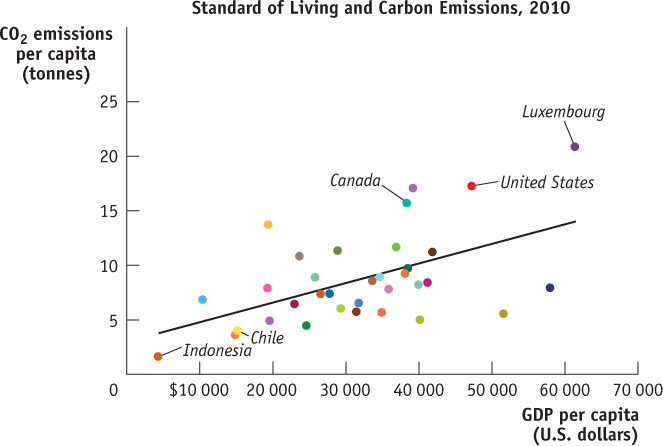
A scatter diagram shows points that correspond to actual observations of the x- and y-variables. A curve is usually fitted to the scatter of points.
Figure 2A-9 is an example of a different kind of numerical graph. It represents information from a sample of 34 countries in a single year on the standard of living, again measured by GDP per capita, and the amount of carbon emissions per capita, a measure of environmental pollution. Each point here indicates an average resident’s standard of living and his or her annual carbon emissions for a given country. The points lying in the upper right of the graph, which show combinations of a high standard of living and high carbon emissions, represent economically advanced countries such as Canada. Points lying in the bottom left of the graph, which show combinations of a low standard of living and low carbon emissions, represent economically less developed countries such as Indonesia and Chile. The pattern of points indicates that there is generally a positive relationship between living standard and carbon emissions per capita: on the whole, people create more pollution in countries with a higher standard of living. This type of graph is called a scatter diagram, a diagram in which each point corresponds to an actual observation of the x-variable and the y-variable. In scatter diagrams, a curve is typically fitted to the scatter of points; that is, a curve is drawn that approximates as closely as possible the general relationship between the variables. As you can see, the fitted line in Figure 2A-9 is upward sloping, indicating the underlying positive relationship between the two variables. Scatter diagrams are often used to show how a general relationship can be inferred from a set of data.
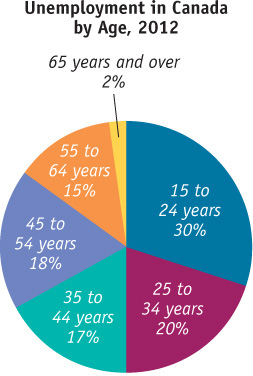
A pie chart shows how some total is divided among its components, usually expressed in percentages.
A pie chart shows the share of a total amount that is accounted for by various components, usually expressed in percentages. For example, Figure 2A-10 is a pie chart that depicts what percentage of all unemployed in Canada in 2012 came from different age groups. The fraction of unemployed is the highest among people in the 15 to 24 years age group; about 30% of the unemployed in 2012 fell into this age group.
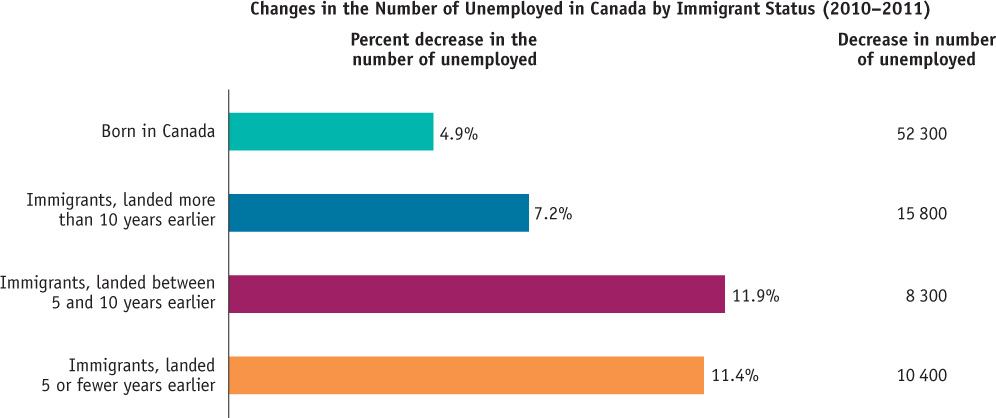
Bar graphs use bars of various heights or lengths to indicate values of a variable. In the bar graph in Figure 2A-11, the bars show the percent change in the number of unemployed workers in Canada between 2010 and 2011 by different immigrant status—
Source: Statistics Canada.
A bar graph uses bars of varying height or length to show the comparative sizes of different observations of a variable.
Problems in Interpreting Numerical Graphs Although the beginning of this appendix emphasized that graphs are visual images that make ideas or information easier to understand, graphs can be constructed (intentionally or unintentionally) in ways that are misleading and can lead to inaccurate conclusions. This section raises some issues that you should be aware of when you interpret graphs.
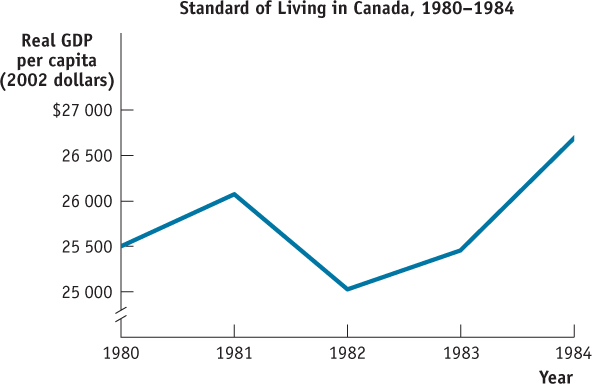
Features of Construction Before drawing any conclusions about what a numerical graph implies, you should pay attention to the scale, or size of increments, shown on the axes. Small increments tend to visually exaggerate changes in the variables, whereas large increments tend to visually diminish them. So the scale used in construction of a graph can influence your interpretation of the significance of the changes it illustrates—
Take, for example, Figure 2A-12, which shows real GDP per capita in Canada from 1980 to 1984 using increments of $500. You can see that real GDP per capita fell from $26 081 in 1981 to $25 035 in 1982. A decrease, sure, but is it as enormous as the scale chosen for the vertical axis makes it seem? If you go back and re-
Source: Statistics Canada.
An axis is truncated when some of the values on the axis are omitted, usually to save space or to make changes to a variable appear larger.
Related to the choice of scale is the use of truncation in constructing a graph. An axis is truncated when part of the range is omitted. This is indicated by two slashes (//) in the axis near the origin. You can see that the vertical axis of Figure 2A-12 has been truncated—
You must also pay close attention to exactly what a graph is illustrating. For example, in Figure 2A-11, you should recognize that what is being shown here are percentage changes in the number of unemployed, not numerical changes. The percentage change in the number of unemployed immigrants landed between 5 and 10 years earlier decreased by the highest percentage, 11.9% in this example. If you were to confuse numerical changes with percentage changes, you would erroneously conclude that the largest absolute reduction of unemployed workers were immigrants landed between 5 and 10 years earlier. But, in fact, Figure 2A-11 shows that the greatest reduction of unemployed workers were those who were born in Canada: the total number of Canadian-
An omitted variable is an unobserved variable that, through its influence on other variables, may create the erroneous appearance of a direct causal relationship among those variables.
Omitted Variables From a scatter diagram that shows two variables moving either positively or negatively in relation to each other, it is easy to conclude that there is a causal relationship. But relationships between two variables are not always due to direct cause and effect. Quite possibly an observed relationship between two variables is due to the unobserved effect of a third variable on each of the other two variables. An unobserved variable that, through its influence on other variables, creates the erroneous appearance of a direct causal relationship among those variables is called an omitted variable. For example, in Manitoba, a greater amount of snowfall during a given week will typically cause people to buy more snow shovels. It will also cause people to buy more lock de-
The error of reverse causality is committed when the true direction of causality between two variables is reversed.
Reverse Causality Even when you are confident that there is no omitted variable and that there is a causal relationship between two variables shown in a numerical graph, you must also be careful that you don’t make the mistake of reverse causality—coming to an erroneous conclusion about which is the dependent and which is the independent variable by reversing the true direction of causality between the two variables. For example, imagine a scatter diagram that depicts the grade point averages (GPAs) of 20 of your classmates on one axis and the number of hours that each of them spends studying on the other. A line fitted between the points will probably have a positive slope, showing a positive relationship between GPA and hours of studying. We could reasonably infer that hours spent studying is the independent variable and that GPA is the dependent variable. But you could make the error of reverse causality: you could infer that a high GPA causes a student to study more, whereas a low GPA causes a student to study less.
The significance of understanding how graphs can mislead or be incorrectly interpreted is not purely academic. Policy decisions, business decisions, and political arguments are often based on interpretation of the types of numerical graphs that we’ve just discussed. Problems of misleading features of construction, omitted variables, and reverse causality can lead to very important and undesirable consequences.