11.4 The Income—Expenditure Model
Earlier in this chapter, we described how autonomous changes in spending—
Before we begin, let’s quickly recap the assumptions underlying the multiplier process.
Changes in overall expenditure (spending) lead to changes in aggregate output. We assume that producers are willing to supply additional output at a fixed price level. As a result, changes in spending translate into changes in output rather than moves of the overall price level up or down. A fixed aggregate price level also implies that there is no difference between nominal GDP and real GDP.1 So we can use the two terms interchangeably in this chapter.
The interest rate is fixed. We’ll take the interest rate as predetermined and unaffected by the factors we analyze in the model. As in the case of the aggregate price level, what we’re really doing here is leaving the determinants of the interest rate outside the model. As we’ll see, the model can still be used to study the effects of a change in the interest rate.
Taxes, government transfers, and government purchases are all zero.
Exports and imports are both zero.
In all subsequent chapters, we will drop the assumption that the aggregate price level is fixed. Appendix 13A addresses how taxes affect the multiplier process. We’ll explain how the interest rate is determined in Chapter 15 and bring foreign trade back into the picture in Chapter 19.
Planned Aggregate Expenditure and Real GDP
In an economy with no government and no foreign trade, there are only two sources of aggregate expenditure: consumer spending, C, and investment spending, I. And since we assume that there are no taxes or transfers, aggregate disposable income, YD, is equal to nominal GDP (which, since the aggregate price level is fixed, is proportional to real GDP): the total value of final sales of goods and services ultimately accrues to households as income. So in this highly simplified economy, there are two basic equations of national income accounting:
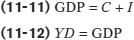
As we learned earlier in this chapter, the aggregate consumption function shows the relationship between disposable income and consumer spending. Let’s continue to assume that the aggregate consumption function is of the same form as in Equation 11-9:
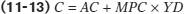
In our simplified model, we will also assume planned investment spending, IPlanned, is autonomous or fixed.
We need one more concept before putting the model together: planned aggregate expenditure, the total amount of planned spending in the economy. Unlike firms, households don’t take unintended actions like unplanned inventory investment. So planned aggregate expenditure is equal to the sum of consumer spending and planned investment spending. We denote planned aggregate expenditure by AEPlanned, so:
Planned aggregate expenditure is the total amount households, businesses, and governments planned to spend.

Substituting in the aggregate consumption, this becomes:

This can be rewritten as:
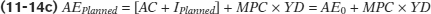
where AE0 represents autonomous planned aggregate expenditure, which collects all of the components of aggregate expenditure that are assumed to be autonomous or fixed. This is the intercept in the planned expenditure line—
The level of planned aggregate expenditure in a given year depends on the level of real GDP in that year. To see why, let’s look at a specific example, shown in Table 11-3. We assume that the aggregate consumption function is:
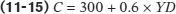
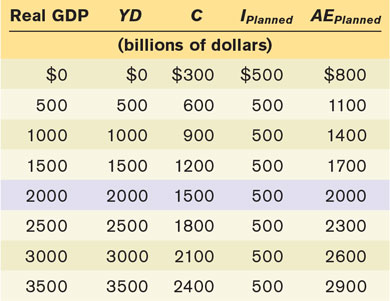
Real GDP, YD, C, IPlanned, and AEPlanned are all measured in billions of dollars, and we assume that the level of planned investment, IPlanned, is fixed at $500 billion per year. The first column shows possible levels of real GDP. The second column shows disposable income, YD, which in our simplified model is equal to real GDP. The third column shows consumer spending, C, equal to $300 billion plus 0.6 times disposable income, YD. The fourth column shows planned investment spending, IPlanned, which we have assumed is $500 billion regardless of the level of real GDP. Finally, the last column shows planned aggregate expenditure, AEPlanned, the sum of aggregate consumer spending, C, and planned investment spending, IPlanned. (To economize on notation, we’ll assume that it is understood from now on that all the variables in Table 11-3 are measured in billions of dollars per year.) As you can see, a higher level of real GDP leads to a higher level of disposable income: every 500 increase in real GDP raises YD by 500, which in turn raises C by 500 × 0.6 = 300 and AEPlanned by 300.
Figure 11-8 illustrates the information in Table 11-3 graphically. Real GDP is measured on the horizontal axis. CF is the aggregate consumption function; it shows how consumer spending depends on real GDP. AEPlanned, the planned aggregate expenditure line, corresponds to the aggregate consumption function shifted up by 500 (the amount of IPlanned). It shows how planned aggregate expenditure depends on real GDP. Both lines have a slope of 0.6, equal to MPC, the marginal propensity to consume.

But this isn’t the end of the story. Table 11-3 reveals that real GDP equals planned aggregate expenditure, AEPlanned, only when the level of real GDP is at 2000. Real GDP does not equal AEPlanned at any other level. Is that possible? Didn’t we learn in Chapter 7, with the circular-
Income–Expenditure Equilibrium
For all but one value of real GDP shown in Table 11-3, real GDP is either more or less than AEPlanned, the sum of consumer spending and planned investment spending. For example, when real GDP is 1000, consumer spending, C, is 900 and planned investment spending is 500, making planned aggregate expenditure 1400. This is 400 more than the corresponding level of real GDP. Now consider what happens when real GDP is 2500; consumer spending, C, is 1800 and planned investment spending is 500, making planned aggregate expenditure only 2300, which is 200 less than real GDP.
As we’ve just explained, planned aggregate expenditure can be different from real GDP only if there is unplanned inventory investment, IUnplanned, in the economy. Let’s examine Table 11-4, which includes the numbers for real GDP and for planned aggregate expenditure from Table 11-3. It also includes the levels of unplanned inventory investment, IUnplanned, that each combination of real GDP and planned aggregate expenditure implies. For example, if real GDP is 2500, planned aggregate expenditure is only 2300. This 200 excess of real GDP over AEPlanned must consist of positive unplanned inventory investment. This can happen only if firms have overestimated sales and produced too much, leading to unintended additions to inventories. More generally, any level of real GDP in excess of 2000 corresponds to a situation in which firms are producing more than consumers and other firms want to purchase, creating an unintended increase in inventories.
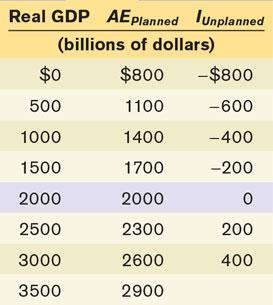
Conversely, a level of real GDP below 2000 implies that planned aggregate expenditure is greater than real GDP. For example, when real GDP is 1000, planned aggregate expenditure is much larger, at 1400. The 400 excess of AEPlanned over real GDP corresponds to negative unplanned inventory investment equal to −400. More generally, any level of real GDP below 2000 implies that firms have underestimated sales, leading to a negative level of unplanned inventory investment in the economy.
By putting together Equations 11-10, 11-11, and 11-14a, we can summarize the general relationships among real GDP, planned aggregate expenditure, and unplanned inventory investment as follows:
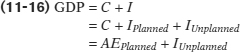
So whenever real GDP exceeds AEPlanned, IUnplanned is positive; whenever real GDP is less than AEPlanned, IUnplanned is negative.
But firms will act to correct their mistakes. We’ve assumed that they don’t change their prices, but they can adjust their output. Specifically, they will reduce production if they have experienced an unintended rise in inventories or increase production if they have experienced an unintended fall in inventories. And these responses will eventually eliminate the unanticipated changes in inventories and move the economy to a point at which real GDP is equal to planned aggregate expenditure. Staying with our example, if real GDP is 1000, negative unplanned inventory investment will lead firms to increase production (by hiring additional workers if necessary), leading to a rise in real GDP. In fact, this will happen whenever real GDP is less than 2000—that is, whenever real GDP is less than planned aggregate expenditure. Conversely, if real GDP is 2500, positive unplanned inventory investment will lead firms to reduce production (perhaps by laying off some of their workers), leading to a fall in real GDP. This will happen whenever real GDP is greater than planned aggregate expenditure.
The economy is in income–expenditure equilibrium when aggregate output, measured by real GDP, is equal to planned aggregate expenditure.
The only situation in which firms won’t have an incentive to change output in the next period is when aggregate output, measured by real GDP, is equal to planned aggregate expenditure in the current period, an outcome known as income–expenditure equilibrium. In Table 11-4, income–
Income–expenditure equilibrium GDP is the level of real GDP at which real GDP equals planned aggregate expenditure.
Figure 11-9 illustrates the concept of income–
Now consider what happens if the economy isn’t in income–
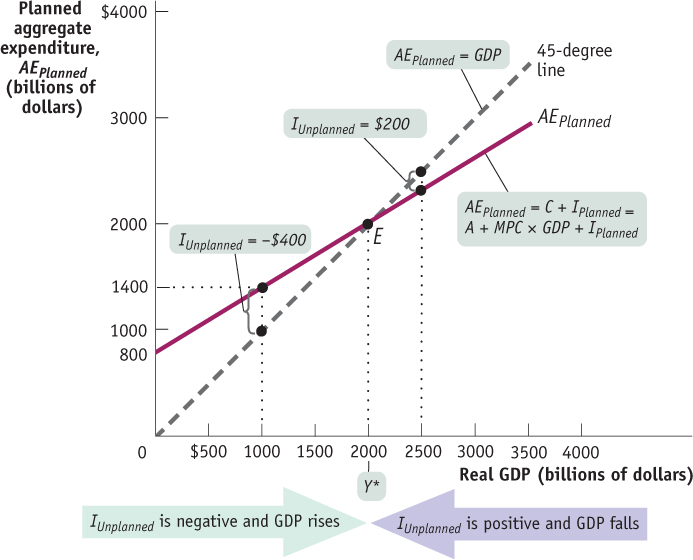
The Keynesian cross diagram identifies income–
The type of diagram shown in Figure 11-9, which identifies income–
The Multiplier Process and Inventory Adjustment
We’ve just learned about a very important feature of the macroeconomy: when planned spending by households and firms does not equal the current aggregate output by firms, this difference shows up as (unplanned) changes in inventories. The response of firms to those inventory changes moves real GDP over time to the point at which real GDP and planned aggregate expenditure are equal. That’s why, as we mentioned earlier, changes in inventories are considered a leading indicator of future economic activity.
Now that we understand how real GDP moves to achieve income–expenditure equilibrium for a given level of planned aggregate expenditure, let’s turn to understanding what happens when there is a shift of the planned aggregate expenditure line. How does the economy move from the initial point of income–expenditure equilibrium to a new point of income–expenditure equilibrium? And what are the possible sources of changes in planned aggregate expenditure?
In our simple model there are only two possible sources of a shift of the planned aggregate expenditure line: a change in planned investment spending, IPlanned, or a shift of the aggregate consumption function, CF. For example, a change in IPlanned can occur because of a change in the interest rate. (Remember, we’re assuming that the interest rate is fixed by factors that are outside the model. But we can still ask what happens when the interest rate changes.) A shift of the aggregate consumption function (that is, a change in its vertical intercept, AC) can occur because of a change in aggregate wealth—say, due to a rise in house prices. When there is a change in autonomous planned aggregate expenditure—when the planned expenditure line shifts (in a parallel manner)—this represents a change in the level of planned aggregate expenditure at any given level of real GDP. Recall from earlier in this chapter that an autonomous change in planned aggregate expenditure is a change in the desired level of spending by firms, households, and government at any given level of real GDP (although we’ve assumed away the government for the time being). How does an autonomous change in planned aggregate expenditure affect real GDP in income–expenditure equilibrium?
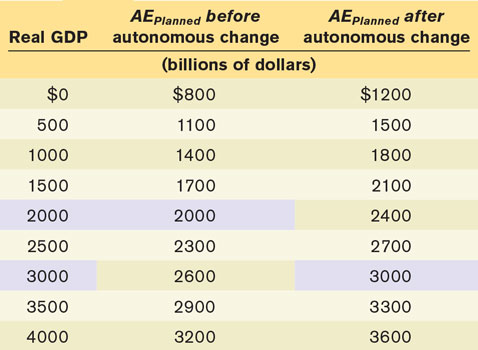
Table 11-5 and Figure 11-10 start from the same numerical example we used in Table 11-4 and Figure 11-9. They also show the effect of an autonomous increase in planned aggregate expenditure of 400, which is what happens when planned aggregate expenditure is 400 higher at each level of real GDP. Look first at Table 11-5. Before the autonomous increase in planned aggregate expenditure, the level of real GDP at which planned aggregate expenditure is equal to real GDP, Y*, is 2000. After the autonomous change, Y* has risen to 3000. The same result is visible in Figure 11-10. The initial income–expenditure equilibrium is at E1, where 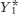 is 2000. The autonomous rise in planned aggregate expenditure shifts the planned aggregate expenditure line up, leading to a new income–expenditure equilibrium at E2, where
is 2000. The autonomous rise in planned aggregate expenditure shifts the planned aggregate expenditure line up, leading to a new income–expenditure equilibrium at E2, where  is 3000.
is 3000.
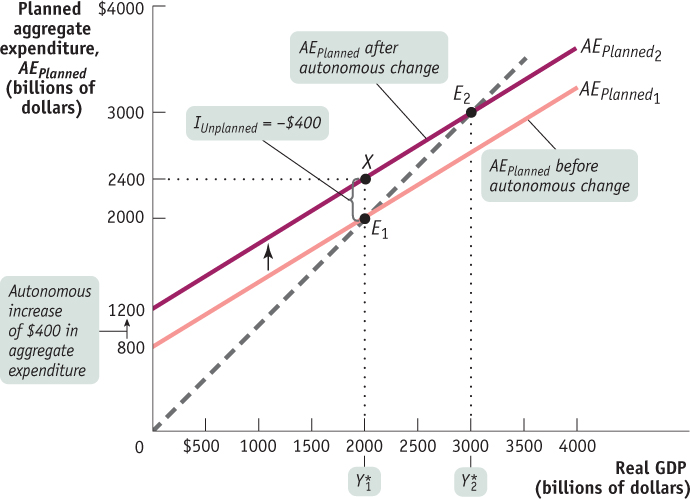
 , equal to 2000. An auton-omous increase in AEPlanned of 400 shifts the planned aggregate expenditure line upward by 400. The economy is no longer in income–expenditure equilibrium: real GDP is equal to 2000 but AEPlanned is now 2400, represented by point X. The vertical distance between the two planned aggregate expenditure lines, equal to 400, represents IUnplanned = −400—the negative inventory investment that the economy now experiences. respond by increasing production, and the economy eventually reaches a new income–expenditure equilibrium at E2 with a higher level of income–expenditure equilibrium GDP,
, equal to 2000. An auton-omous increase in AEPlanned of 400 shifts the planned aggregate expenditure line upward by 400. The economy is no longer in income–expenditure equilibrium: real GDP is equal to 2000 but AEPlanned is now 2400, represented by point X. The vertical distance between the two planned aggregate expenditure lines, equal to 400, represents IUnplanned = −400—the negative inventory investment that the economy now experiences. respond by increasing production, and the economy eventually reaches a new income–expenditure equilibrium at E2 with a higher level of income–expenditure equilibrium GDP, 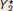 , equal to 3000.
, equal to 3000.The fact that the rise in income–expenditure equilibrium GDP, from 2000 to 3000, is much larger than the autonomous increase in aggregate expenditure, which is only 400, has a familiar explanation: the multiplier process. In the specific example we have just described, an autonomous increase in planned aggregate expenditure of 400 leads to an increase in Y* from 2000 to 3000, a rise of 1000. So the multiplier in this example is 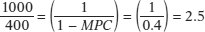 .
.
We can examine in detail what underlies the multi-stage multiplier process by looking more closely at Figure 11-10. First, starting from E1, the autonomous increase in planned aggregate expenditure leads to a gap between planned aggregate expenditure and real GDP. This is represented by the vertical distance between X, at 2400, and E1, at 2000. This gap illustrates an unplanned fall in inventory investment: IUnplanned = −400. Firms respond by increasing production, leading to a rise in real GDP from 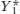 . The rise in real GDP translates into an increase in disposable income, YD. That’s the first stage in the chain reaction. But it doesn’t stop there—the increase in YD leads to a rise in consumer spending, C, which sets off a second-round rise in real GDP. This in turn leads to a further rise in disposable income and consumer spending, and so on. And we could play this process in reverse: an autonomous fall in aggregate expenditure will lead to a chain reaction of reductions in production, causing a fall in real GDP and consumer spending.
. The rise in real GDP translates into an increase in disposable income, YD. That’s the first stage in the chain reaction. But it doesn’t stop there—the increase in YD leads to a rise in consumer spending, C, which sets off a second-round rise in real GDP. This in turn leads to a further rise in disposable income and consumer spending, and so on. And we could play this process in reverse: an autonomous fall in aggregate expenditure will lead to a chain reaction of reductions in production, causing a fall in real GDP and consumer spending.
We can summarize these results in an equation, where ΔAE0 represents a change in the autonomous portion of planned expenditure, AEPlanned, and 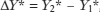 , the subsequent change in income–expenditure equilibrium GDP:
, the subsequent change in income–expenditure equilibrium GDP:
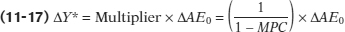
Recalling that the multiplier, 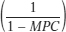 , is greater than 1, Equation 11-17 tells us that the change in income–expenditure equilibrium GDP, ΔY*, is several times as large as the autonomous change in planned aggregate expenditure, ΔAE0. It also helps us recall an important point: because the marginal propensity to consume is less than 1, each increase in disposable income and each corresponding increase in consumer spending is smaller than in the previous round. That’s because at each round some of the increase in disposable income leaks out into savings. As a result, although real GDP grows at each round, the increase in real GDP diminishes from each round to the next. At some point the increase in real GDP is negligible, and the economy converges to a new income–expenditure equilibrium GDP at
, is greater than 1, Equation 11-17 tells us that the change in income–expenditure equilibrium GDP, ΔY*, is several times as large as the autonomous change in planned aggregate expenditure, ΔAE0. It also helps us recall an important point: because the marginal propensity to consume is less than 1, each increase in disposable income and each corresponding increase in consumer spending is smaller than in the previous round. That’s because at each round some of the increase in disposable income leaks out into savings. As a result, although real GDP grows at each round, the increase in real GDP diminishes from each round to the next. At some point the increase in real GDP is negligible, and the economy converges to a new income–expenditure equilibrium GDP at  .
.
The Paradox of Thrift You may recall that in Chapter 6 we mentioned the paradox of thrift to illustrate the fact that in macroeconomics the outcome of many individual actions can generate a result that is different from and worse than the simple sum of those individual actions. In the paradox of thrift, when households and firms anticipate tough(er) economic times, they attempt to save more. These actions depress the economy, leaving households and firms worse off than if they hadn’t acted virtuously to prepare for tough times. It is called a paradox because what’s usually “good” (saving to provide for your family in hard times) is “bad” (because it can make everyone worse off).
Using the multiplier, we can now see exactly how this scenario unfolds. Suppose that there is a slump in consumer spending or investment spending, or both, just like the slump in residential construction investment spending leading up to the 2008–2009 recession. This causes a fall in income–expenditure equilibrium GDP that is several times larger than the original fall in spending. The fall in real GDP leaves consumers and producers worse off than they would have been if they hadn’t cut their spending. Conversely, prodigal behaviour is rewarded: if consumers or producers increase their spending, the resulting multiplier process makes the increase in income–expenditure equilibrium GDP several times larger than the original increase in spending. So prodigal spending makes consumers and producers better off than if they had been cautious spenders.

It’s important to realize that our result that the multiplier is equal to 1/(1 − MPC) depends on the simplifying assumptions that there are no taxes or transfers and that planned investment does not depend directly on GDP, so that disposable income is equal to real GDP. In Appendix 13A, we’ll bring taxes into the picture, which makes the expression for the multiplier more complicated and the multiplier itself smaller. But the general principle we have just learned—an autonomous change in planned aggregate expenditure leads to a change in income–expenditure equilibrium GDP, both directly and through an induced change in consumer spending—remains valid.
As we noted earlier in this chapter, declines in planned investment spending are usually the major factor causing recessions, because historically they have been the most common source of autonomous reductions in aggregate expenditure. The tendency of the consumption function to shift upward over time, which we pointed out earlier in Economics in Action, “Famous First Forecasting Failures,” means that autonomous changes in both planned investment spending and consumer spending play important roles in expansions. But regardless of the source, there are multiplier effects in the economy that magnify the size of the initial change in aggregate expenditure.
INVENTORIES AND THE END OF A RECESSION
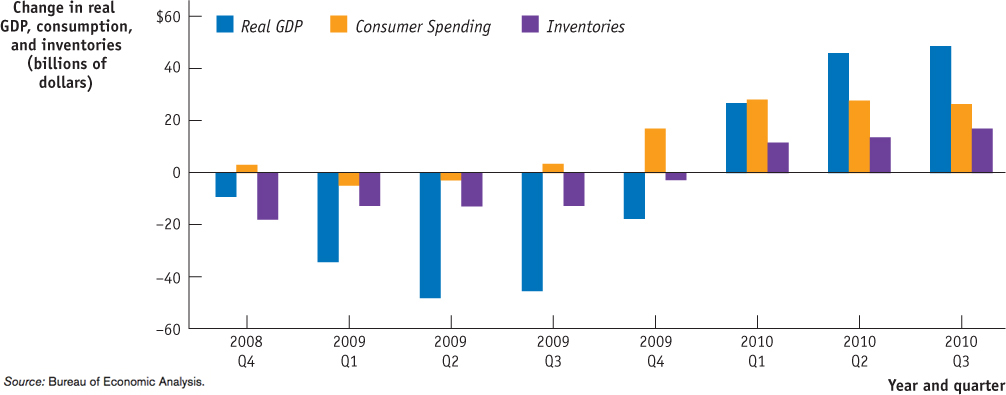
A very clear example of the role of inventories in the multiplier process took place in the 2008–2009 recession. One of the driving forces behind the recession was a slump in business investment spending. It took several quarters before investment spending bounced back in the form of a renewed housing boom and the building of infrastructure funded under the Economic Action Plan.
Source: Bureau of Economic Analysis.
Figure 11-11 shows changes in real GDP, real consumer spending, and real inventories by quarter from the fourth quarter of 2008 to the third quarter of 2010. Notice in the last quarter of 2008 how the fall in inventories exceeded the drop in real GDP, showing that this decrease was a driving force behind the recession. Consumer spending began to increase in the second quarter of 2009, but it was not until the first quarter of 2010 that GDP was positive. You might ask, why was that the case? The answer is rather simple. In the third quarter of 2009, the recession was still in full force and suppliers were reluctant to ramp up production too quickly and get caught in a difficult position. It wasn’t until the first quarter of 2010 that inventories were positive.

Quick Review
The economy is in income–expenditure equilibrium when planned aggregate expenditure is equal to real GDP.
At any output level greater than income–expenditure equilibrium GDP, real GDP exceeds planned aggregate expenditure and inventories are rising. At any lower output level, real GDP falls short of planned aggregate expenditure and inventories are falling.
After an autonomous change in planned aggregate expenditure, the economy moves to a new income–expenditure equilibrium through the inventory adjustment process, as illustrated by the Keynesian cross. Because of the multiplier effect, the change in income– expenditure equilibrium GDP is a multiple of the autonomous change in aggregate expenditure.
Check Your Understanding 11-4
CHECK YOUR UNDERSTANDING 11-4
Although economists believe that recessions typically begin as slumps in investment spending, they also believe that consumer spending eventually slumps during a recession. Explain why.
A slump in planned investment spending will lead to a fall in real GDP in response to an unanticipated increase in inventories. The fall in real GDP will translate into a fall in households’ disposable income, and households will respond by reducing consumer spending. The decrease in consumer spending leads producers to further decrease output, further lowering disposable income and leading to further reductions in consumer spending. So although the slump originated in investment spending, it will cause a reduction in consumer spending.
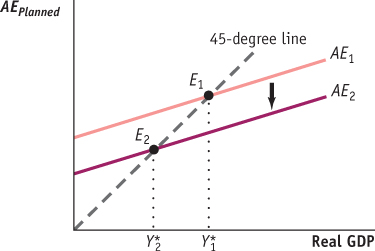
Use a diagram like Figure 11-10 to show what happens when there is an autonomous fall in planned aggregate expenditure. Describe how the economy adjusts to a new income–expenditure equilibrium.
Suppose Y* is originally $500 billion, the autonomous reduction in planned aggregate expenditure is $300 million ($0.3 billion), and MPC = 0.5. Calculate Y* after such a change.
After an autonomous fall in planned aggregate expenditure, the economy is no longer in equilibrium: real GDP is greater than planned aggregate expenditure. The accompanying figure shows this autonomous fall in planned aggregate expenditure by the shift of the aggregate expenditure curve from AE1 to AE2. The difference between the two results in positive unplanned inventory investment: there is an unanticipated increase in inventories. Firms will respond by reducing production. This will eventually move the economy to a new equilibrium. In the accompanying figure, this is illustrated by the movement from the initial income–expenditure equilibrium at E1 to the new income–expenditure equilibrium at E2. As the economy moves to its new equilibrium, real GDP falls from its initial income–expenditure equilibrium level at
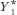 to its new lower level,
to its new lower level, 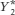 .
.
We know that the change in income–expenditure equilibrium GDP is given by Equation 11-17: ΔY* = Multiplier × ΔAAEPlanned. Here, the multiplier = 1/(1 – 0.5) = 1/0.5 = 2. So a $300 million autonomous reduction in planned aggregate expenditure will lead to a 2 × $300 million = $600 million ($0.6 billion) fall in income–expenditure equilibrium GDP. The new Y* will be $500 billion – $0.6 billion = $499.4 billion.
Keeping Afloat in Newfoundland and Labrador

St. John’s, the capital of Newfoundland and Labrador, is a large city with many stores and industries that are not related directly to the cod industry. So you might think that the local businesses in St. John’s would have been less affected by the moratorium than the small outport fishing communities.
In fact, all of St. John’s suffered. Many stores went out of business, and others came close to it. Consider Templeton’s, a local family-owned store that has been in operation in St John’s for almost a century and a half. Originally an importer of dry goods from Europe and the United States (remember, Newfoundland did not join Canada until 1949), Templeton’s decided to specialize in 1922, and since that time it has been the place to shop for paint, wallpaper, and floor coverings. But despite its history and longevity, Templeton’s sales fell drastically during the moratorium, and the situation was dire.
The story does have a happy ending though. Templeton’s raised its sales by introducing a popular new line of paint in unique colours that reflected the heritage of the province, such as Dory Buff, Iceberg Alley, and Mussels in the Corner. Similarly, other entrepreneurs looked to tourism opportunities in response to the cod moratorium, starting iceberg and whale-watching tours and opening shops featuring local jams and heritage crafts. These businesses have also prospered. But of course the main reason for the economic boom in Newfoundland and Labrador is the development of the huge oil deposits off the coast. In 2012, St. John’s economy was described as “sizzling,” with a GDP of nearly $52 000 per capita, the second best in Canada.2 And housing starts, a sure indicator of prosperity, had risen, from a low of 1371 in 1999 to 3488 in 2011.3
QUESTIONS FOR THOUGHT
Why did a moratorium on cod fishing affect stores like Templeton’s, which sells paint and flooring?
Why did a moratorium on cod fishing affect stores like Templeton’s, which sells paint and flooring?
Why would the number of housing starts be related to the new economic developments in oil and tourism?
Why would the number of housing starts be related to the new economic developments in oil and tourism?
