1.2 Module 9: Interpreting Price Elasticity of Demand

iStockphoto/Thinkstock

A Closer Look at the Price Elasticity of Demand

Med-Stat and other pharmaceutical distributors believed they could sharply drive up flu vaccine prices in the face of a shortage because the price elasticity of vaccine demand was low. But what does that mean? How low does a price elasticity have to be for us to classify it as low? How high does it have to be for us to consider it high? And what determines whether the price elasticity of demand is high or low, anyway? To answer these questions, we need to look more deeply at the price elasticity of demand.

How Elastic Is Elastic?

As a first step toward classifying price elasticities of demand, let’s look at the extreme cases.

First, consider the demand for a good when people pay no attention to the price of, say, shoelaces. Suppose that consumers would buy 1 billion pairs of shoelaces per year regardless of the price. If that were true, the demand curve for shoelaces would look like the curve shown in panel (a) of Figure 9-1: it would be a vertical line at 1 billion pairs of shoelaces. Since the percent change in the quantity demanded is zero for any change in the price, the price elasticity of demand in this case is zero. The case of a zero price elasticity of demand is known as perfectly inelastic demand.

Panel (a) shows a perfectly inelastic demand curve, which is a vertical line. The quantity of shoelaces demanded is always 1 billion pairs, regardless of price. As a result, the price elasticity of demand is zero—the quantity demanded is unaffected by the price. Panel (b) shows a perfectly elastic demand curve, which is a horizontal line. At a price of $5, consumers will buy any quantity of pink tennis balls, but will buy none at a price above $5. If the price falls below $5, they will buy an extremely large number of pink tennis balls and none of any other color.

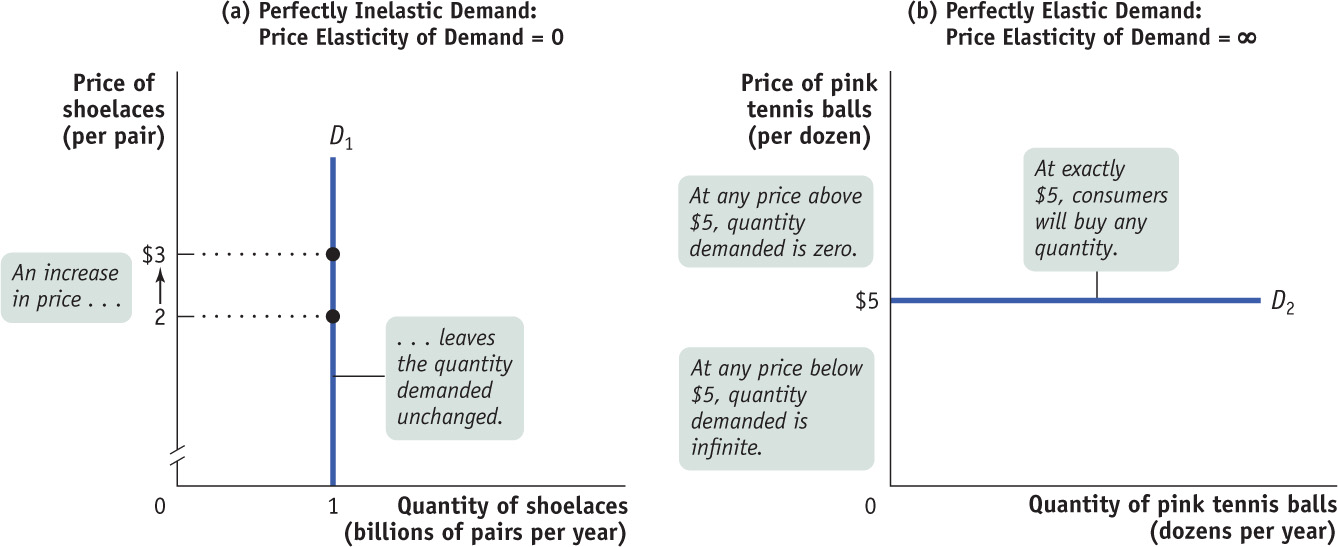
The opposite extreme occurs when even a tiny rise in the price will cause the quantity demanded to drop to zero or even a tiny fall in the price will cause the quantity demanded to get extremely large.

Panel (b) of Figure 9-1 shows the case of pink tennis balls; we suppose that tennis players really don’t care what color their balls are and that other colors, such as neon green and vivid yellow, are available at $5 per dozen balls. In this case, consumers will buy no pink balls if they cost more than $5 per dozen but will buy only pink balls if they cost less than $5. The demand curve will therefore be a horizontal line at a price of $5 per dozen balls. As you move back and forth along this line, there is a change in the quantity demanded but no change in the price. When you divide a number by zero, you get infinity, denoted by the symbol ∞. So a horizontal demand curve implies an infinite price elasticity of demand. When the price elasticity of demand is infinite, economists say that demand is perfectly elastic.

The price elasticity of demand for the vast majority of goods is somewhere between these two extreme cases. Economists use one main criterion for classifying these intermediate cases: they ask whether the price elasticity of demand is greater or less than 1. When the price elasticity of demand is greater than 1, economists say that demand is elastic. When the price elasticity of demand is less than 1, they say that demand is inelastic. The borderline case is unit-elastic demand, where the price elasticity of demand is—surprise—exactly 1.

Knowing the price elasticity of demand allows the highway department to determine the drop in bridge use that would result from higher tolls.

©Rorem/Dreamstime.com

To see why a price elasticity of demand equal to 1 is a useful dividing line, let’s consider a hypothetical example: a toll bridge operated by the state highway department. Other things being equal, the number of drivers who use the bridge depends on the toll, the price the highway department charges for crossing the bridge: the higher the toll, the fewer the drivers who use the bridge.

Figure 9-2 shows three hypothetical demand curves—one in which demand is unit-elastic, one in which it is inelastic, and one in which it is elastic. In each case, point A shows the quantity demanded if the toll is $0.90 and point B shows the quantity demanded if the toll is $1.10. An increase in the toll from $0.90 to $1.10 is an increase of 20% if we use the midpoint method to calculate percent changes.

Panel (a) shows a case of unit-elastic demand: a 20% increase in price generates a 20% decline in quantity demanded, representing a price elasticity of demand of 1. Panel (b) shows a case of inelastic demand: a 20% increase in price generates a 10% decline in quantity demanded, representing a price elasticity of demand of 0.5. A case of elastic demand is shown in Panel (c): a 20% increase in price causes a 40% decline in quantity demanded, representing a price elasticity of demand of 2. All percentages are calculated using the midpoint method.

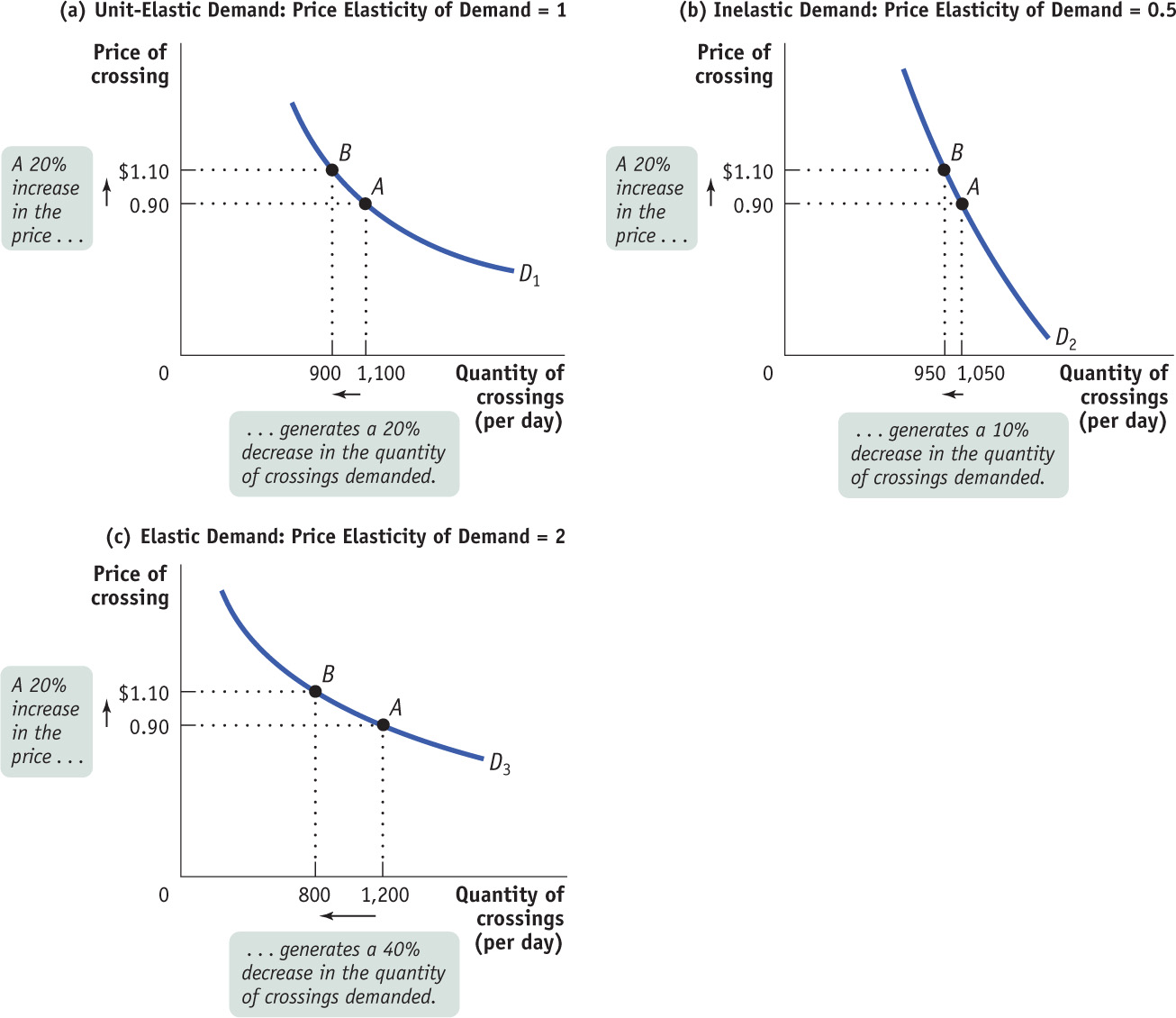
Panel (a) shows what happens when the toll is raised from $0.90 to $1.10 and the demand curve is unit-elastic. Here the 20% price rise leads to a fall in the quantity of cars using the bridge each day from 1,100 to 900, which is a 20% decline (again using the midpoint method). So the price elasticity of demand is 20%/20% = 1.

Panel (b) shows a case of inelastic demand when the toll is raised from $0.90 to $1.10. The same 20% price rise reduces the quantity demanded from 1,050 to 950. That’s only a 10% decline, so in this case the price elasticity of demand is 10%/20% = 0.5.

Panel (c) shows a case of elastic demand when the toll is raised from $0.90 to $1.10. The 20% price increase causes the quantity demanded to fall from 1,200 to 800, a 40% decline, so the price elasticity of demand is 40%/20% = 2.

Why does it matter whether demand is unit-elastic, inelastic, or elastic? Because this classification predicts how changes in the price of a good will affect the total revenue earned by producers from the sale of that good. In many real-life situations, such as the one faced by Med-Stat, it is crucial to know how price changes affect total revenue. Total revenue is defined as the total value of sales of a good or service: the price multiplied by the quantity sold.

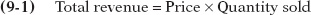
Total revenue has a useful graphical representation that can help us understand why knowing the price elasticity of demand is crucial when we ask whether a price rise will increase or reduce total revenue. Panel (a) of Figure 9-3 shows the same demand curve as panel (a) of Figure 9-2. We see that 1,100 drivers will use the bridge if the toll is $0.90. So the total revenue at a price of $0.90 is $0.90 × 1,100 = $990. This value is equal to the area of the green rectangle, which is drawn with the bottom left corner at the point (0, 0) and the top right corner at (1,100, 0.90). In general, the total revenue at any given price is equal to the area of a rectangle whose height is the price and whose width is the quantity demanded at that price.

The green rectangle in panel (a) represents total revenue generated from 1,100 drivers who each pay a toll of $0.90. Panel (b) shows how total revenue is affected when the price increases from $0.90 to $1.10. Due to the quantity effect, total revenue falls by area A. Due to the price effect, total revenue increases by area C. In general, the overall effect can go either way, depending on the price elasticity of demand.

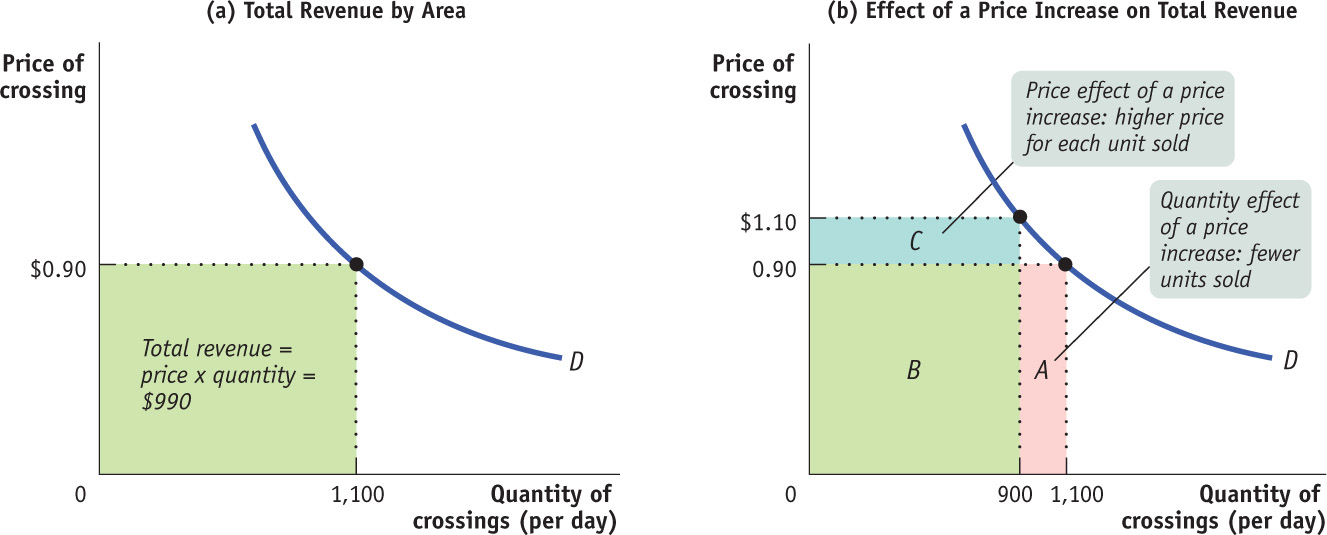
To get an idea of why total revenue is important, consider the following scenario. Suppose that the toll on the bridge is currently $0.90 but that the highway department must raise extra money for road repairs. One way to do this is to raise the toll on the bridge. But this plan might backfire, since a higher toll will reduce the number of drivers who use the bridge. And if traffic on the bridge dropped a lot, a higher toll would actually reduce total revenue instead of increasing it. So it’s important for the highway department to know how drivers will respond to a toll increase.

We can see graphically how the toll increase affects total bridge revenue by examining panel (b) of Figure 9-3. At a toll of $0.90, total revenue is given by the sum of the areas A and B. After the toll is raised to $1.10, total revenue is given by the sum of areas B and C. So when the toll is raised, revenue represented by area A is lost but revenue represented by area C is gained.

These two areas have important interpretations. Area C represents the revenue gain that comes from the additional $0.20 paid by drivers who continue to use the bridge. That is, the 900 drivers who continue to use the bridge contribute an additional $0.20 × 900 = $180 per day to total revenue, represented by area C. But 200 drivers who would have used the bridge at a price of $0.90 no longer do so, generating a loss to total revenue of $0.90 × 200 = $180 per day, represented by area A. (In this particular example, because demand is unit-elastic between the two points—the same as in panel (a) of Figure 9-2—the rise in the toll has no effect on total revenue; areas A and C are the same size.)

Except in the rare case of a good with perfectly elastic or perfectly inelastic demand, when a seller raises the price of a good, two countervailing effects are present:

• A price effect. After a price increase, each unit sold sells at a higher price, which tends to raise revenue.
• A quantity effect. After a price increase, fewer units are sold, which tends to lower revenue.

But then, you may ask, what is the net ultimate effect on total revenue: does it go up or down? The answer is that, in general, the effect on total revenue can go either way—a price rise may either increase total revenue or lower it. If the price effect, which tends to raise total revenue, is the stronger of the two effects, then total revenue goes up. If the quantity effect, which tends to reduce total revenue, is the stronger, then total revenue goes down. And if the strengths of the two effects are exactly equal—as in our toll bridge example, where a $180 gain offsets a $180 loss—total revenue is unchanged by the price increase.

The price elasticity of demand tells us what happens to total revenue when price changes: its size determines which effect—the price effect or the quantity effect—is stronger. Specifically:

• If demand for a good is unit-elastic (the price elasticity of demand is 1), an increase in price does not change total revenue. In this case, the quantity effect is weaker than the price effect.
• If demand for a good is inelastic (the price elasticity of demand is less than 1), a higher price increases total revenue. In this case, the quantity effect is weaker than the price effect.
• If demand for a good is elastic (the price elasticity of demand is greater than 1), an increase in price reduces total revenue. In this case, the quantity effect is stronger than the price effect.

Table 9-1 shows how the effect of a price increase on total revenue depends on the price elasticity of demand, using the same data as in Figure 9-2. An increase in the price from $0.90 to $1.10 leaves total revenue unchanged at $990 when demand is unit--elastic. When demand is inelastic, the quantity effect is dominated by the price effect; the same price increase leads to an increase in total revenue from $945 to $1,045. And when demand is elastic, the quantity effect dominates the price effect; the price increase leads to a decline in total revenue from $1,080 to $880.

The price elasticity of demand also predicts the effect of a fall in price on total revenue. When the price falls, the same two countervailing effects are present, but they work in the opposite directions as compared to the case of a price rise. There is the price effect of a lower price per unit sold, which tends to lower revenue. This is countered by the quantity effect of more units sold, which tends to raise revenue. Which effect dominates depends on the price elasticity. Here is a quick summary:

• When demand is unit-elastic, the two effects exactly balance each other out; so a fall in price has no effect on total revenue.
• When demand is inelastic, the quantity effect is dominated by the price effect; so a fall in price reduces total revenue.
• When demand is elastic, the quantity effect dominates the price effect; so a fall in price increases total revenue.

Price Elasticity Along the Demand Curve

Suppose an economist says that “the price elasticity of demand for coffee is 0.25.” What he or she means is that at the current price the elasticity is 0.25. In the previous discussion of the toll bridge, what we were really describing was the elasticity at a specific price. Why this qualification? Because for the vast majority of demand curves, the price elasticity of demand at one point along the curve is different from the price elasticity of demand at other points along the same curve.

To see this, consider the table in Figure 9-4, which shows a hypothetical demand schedule. It also shows in the last column the total revenue generated at each price and quantity combination in the demand schedule. The upper panel of the graph in Figure 9-4 shows the corresponding demand curve. The lower panel illustrates the same data on total revenue: the height of a bar at each quantity demanded—which corresponds to a particular price—measures the total revenue generated at that price.

The upper panel shows a demand curve corresponding to the demand schedule in the table. The lower panel shows how total revenue changes along that demand curve: at each price and quantity combination, the height of the bar represents the total revenue generated. You can see that at a low price, raising the price increases total revenue. So demand is inelastic at low prices. At a high price, however, a rise in price reduces total revenue. So demand is elastic at high prices.

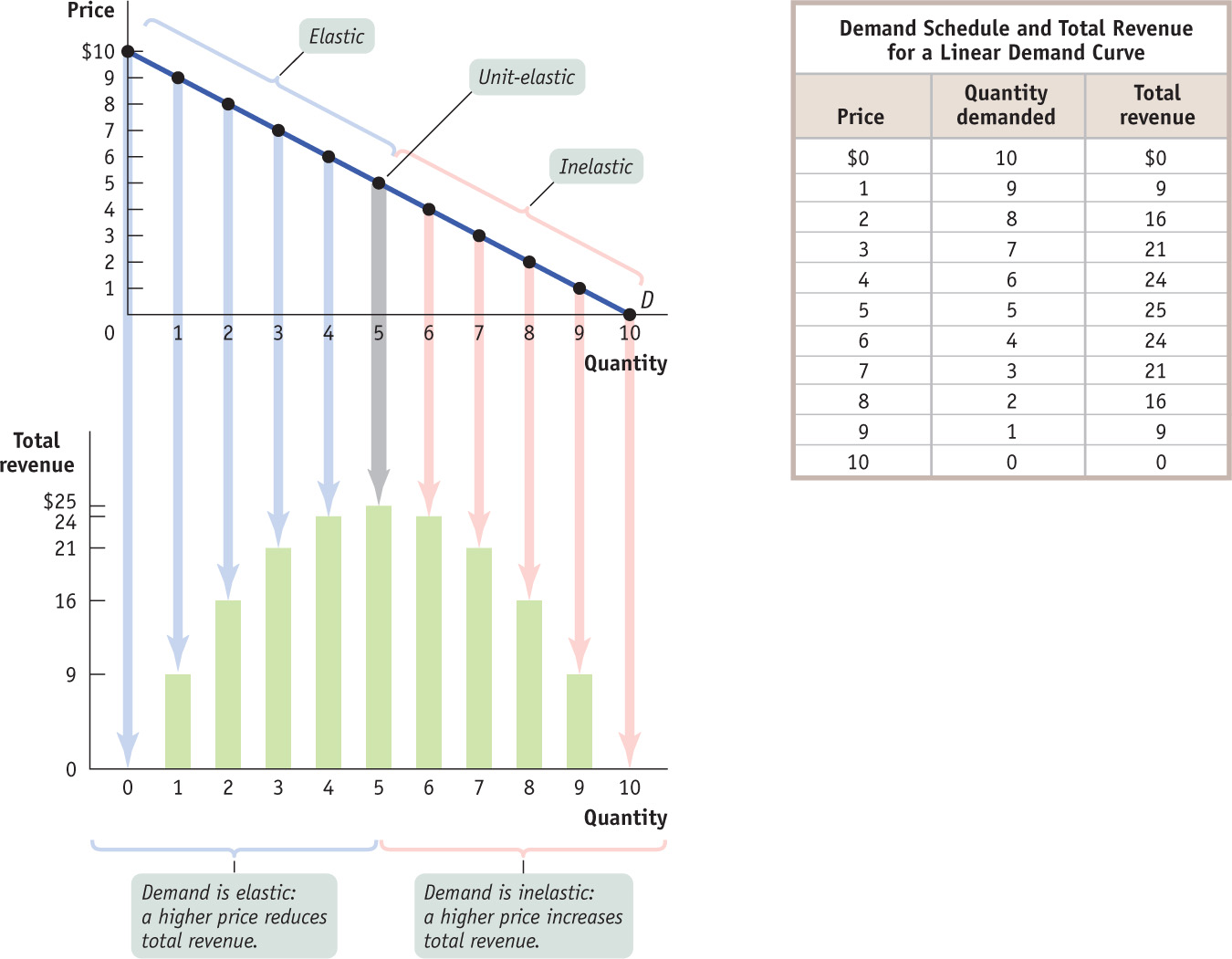
In Figure 9-4, you can see that when the price is low, raising the price increases total revenue: starting at a price of $1, raising the price to $2 increases total revenue from $9 to $16. This means that when the price is low, demand is inelastic. Moreover, you can see that demand is inelastic on the entire section of the demand curve from a price of $0 to a price of $5.

When the price is high, however, raising it further reduces total revenue: starting at a price of $8, for example, raising the price to $9 reduces total revenue, from $16 to $9. This means that when the price is high, demand is elastic. Furthermore, you can see that demand is elastic over the section of the demand curve from a price of $5 to $10.

For the vast majority of goods, the price elasticity of demand changes along the demand curve. So whenever you measure a good’s elasticity, you are really measuring it at a particular point or section of the good’s demand curve.

What Factors Determine the Price Elasticity of Demand?

The flu vaccine shortfall of 2004–2005 allowed vaccine distributors to significantly raise their prices for two important reasons: there were no substitutes, and for many people the vaccine was a medical necessity.

People responded in various ways. Some paid the high prices, and some traveled to Canada and other countries to get vaccinated. Some simply did without (and over time often changed their habits to avoid catching the flu, such as eating out less often and avoiding mass transit). This experience illustrates the four main factors that determine elasticity: whether close substitutes are available, whether the good is a necessity or a luxury, the share of income a consumer spends on the good, and how much time has elapsed since the price change. We’ll briefly examine each of these factors.

Whether Close Substitutes are AvailableThe price elasticity of demand tends to be high if there are other goods that consumers regard as similar and would be willing to consume instead. The price elasticity of demand tends to be low if there are no close substitutes.

Whether the Good is a Necessity Or a LuxuryThe price elasticity of demand tends to be low if a good is something you must have, like a life-saving medicine. The price elasticity of demand tends to be high if the good is a luxury—something you can easily live without.

Share of Income Spent on the GoodThe price elasticity of demand tends to be low when spending on a good accounts for a small share of a consumer’s income. In that case, a significant change in the price of the good has little impact on how much the consumer spends. In contrast, when a good accounts for a significant share of a consumer’s spending, the consumer is likely to be very responsive to a change in price. In this case, the price elasticity of demand is high.

TimeIn general, the price elasticity of demand tends to increase as consumers have more time to adjust to a price change. This means that the long-run price elasticity of demand is often higher than the short-run elasticity.

David Sipress/The New Yorker Collection/www.cartoonbank.com

A good illustration of the effect of time on the elasticity of demand is drawn from the 1970s, the first time gasoline prices increased dramatically in the United States. Initially, consumption fell very little because there were no close substitutes for gasoline and because driving their cars was necessary for people to carry out the ordinary tasks of life. Over time, however, Americans changed their habits in ways that enabled them to gradually reduce their gasoline consumption (by buying more fuel-efficient cars and forming carpools, for example). The result was a steady decline in gasoline consumption over the next decade, even though the price of gasoline did not continue to rise, confirming that the long-run price elasticity of demand for gasoline was indeed much larger than the short-run elasticity.

RESPONDING TO YOUR TUITION BILL

College costs more than ever—and not just because of overall inflation. Tuition has been rising faster than the overall cost of living for years. But does rising tuition keep people from going to college? Two studies found that the answer depends on the type of college. Both studies assessed how responsive the decision to go to college is to a change in tuition.

A 1988 study found that a 3% increase in tuition led to an approximately 2% fall in the number of students enrolled at four-year institutions, giving a price elasticity of demand of 0.67 (2%/3%). In the case of two-year institutions, the study found a significantly higher response: a 3% increase in tuition led to a 2.7% fall in enrollments, giving a price elasticity of demand of 0.9. In other words, the enrollment decision for students at two-year colleges was significantly more responsive to price than for students at four-year colleges. The result: students at two-year colleges are more likely to forgo getting a degree because of tuition costs than students at four-year colleges.

How responsive are college enrollment rates to changes in tuition?

Photodisc

A 1999 study confirmed this pattern. In comparison to four-year colleges, it found that two-year college enrollment rates were significantly more responsive to changes in state financial aid (a decline in aid leading to a decline in enrollments), a predictable effect given these students’ greater sensitivity to the cost of tuition. Another piece of evidence suggests that students at two-year colleges are more likely to be paying their own way and making a trade-off between attending college and working: the study found that enrollments at two-year colleges are much more responsive to changes in the unemployment rate (an increase in the unemployment rate leading to an increase in enrollments) than enrollments at four-year colleges. So is the cost of tuition a barrier to getting a college degree in the United States? Yes, but more so at two-year colleges than at four-year colleges.

Interestingly, the 1999 study found that for both two-year and four-year colleges, price sensitivity of demand had fallen somewhat since the 1988 study. One possible explanation is that because the value of a college education has risen considerably over time, fewer people forgo college, even if tuition goes up.

Module 9 Review

Check Your Understanding

Draw a correctly labeled graph illustrating a demand curve that is a straight line and is neither perfectly elastic nor perfectly inelastic.