In the example discussed in the preceding paragraphs, an initial population of 80 individuals increased by 20 per year over 2 years, for a per capita rate of increase of 0.25 per year. If this per capita rate of increase were to continue, how large would the population be after 10 years? We can answer this question using the following formula:

N_t = N₀ (1 + r)^t

Solving the equation for our example shows that in 10 years the population size would be 745 (1.25 raised to the 10th power, times 80). After 15 years, the population would swell to 2273.

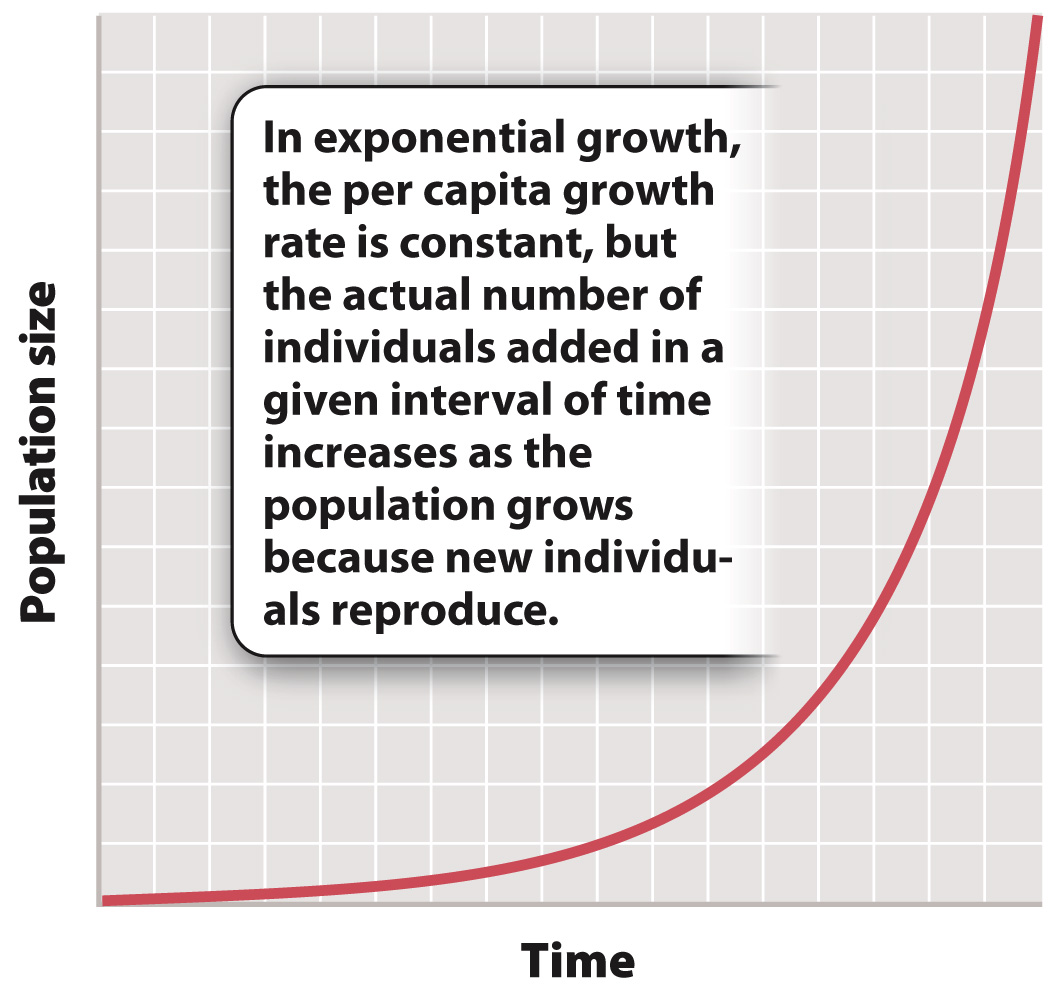
This example illustrates exponential growth, the pattern of population increase that results when r is constant through time. A prominent feature of exponential growth is that the number of individuals added to the population in any time interval is proportional to the size of the population at the start of the interval. That is, while the per capita growth rate remains constant, the actual number of individuals added per time unit increases as the population grows. This is because the individuals added also reproduce, so through time more and more individuals contribute to the growing population. Fig. 46.5 shows the characteristic shape of an exponential growth curve.

A second example brings home the remarkable consequences of exponential growth. Suppose we place one grain of wheat on the first square of an 8 × 8 chessboard that has 64 squares, two on the second square, four on the third, and keep doubling the number at each successive square. By the time we reach the 64th square, the total number of grains on the board is 18,446,744,073,709,551,615, more than 80 times what Earth could produce in a year if wheat were planted on every square inch of farmland, and about a million times the number of stars in the Milky Way galaxy.

Quick Check 2 Would you rather have a million dollars today, or start with one cent and double the amount each day for a month? Why?

The per capita growth rate, r, at any instant is the intrinsic growth rate of a population, the maximum rate of growth when no environmental factors limit population increase. Intrinsic growth rates in mammals range from 82% per year in muskrats to 50% in snowshoe hares and 10% in moose.

Malthus recognized that exponential growth cannot continue for long in nature because the number of individuals eventually outstrips the resources available to support the population. Darwin, in turn, recognized that when the number of young produced at birth exceeds the number of adults that can be supported by available resources, individuals within the population compete to obtain the resources needed for growth and reproduction. This intraspecific (within-species) competition results in natural selection (Chapter 21).

Individuals can also compete for resources with individuals from different species. Such interspecific (between-species) competition can result in an increase or decrease in population size. We focus for the most part on intraspecific competition in this chapter, reserving a detailed discussion of the effects of interspecific competition until Chapter 47.