What is a two-way ANOVA?

What is a factor?

In your own words, define the word cell, first as you would use it in everyday conversation and then as a statistician would use it.

What is a four-way within-groups ANOVA?

What is the difference in information provided when we say two-way ANOVA versus 2 × 3 ANOVA?

What are the three different F statistics in a two-way ANOVA?

What is a marginal mean?

What are the three ways to identify a statistically significant interaction?

How do bar graphs help us identify and interpret interactions? Explain how adding lines to the bar graph can help.

How do we calculate the between-groups degrees of freedom for an interaction?

In step 6 of hypothesis testing for a two-way between-groups ANOVA, we make a decision for each F statistic. What are the three possible outcomes with respect to the overall pattern of results?

When are post hoc tests needed for a two-way between-groups ANOVA?

Explain the following formula in your own words: SS_interaction = SS_total − (SS_rows + SS_columns + SS_within).

In your own words, define the word interaction, first as you would use it in everyday conversation and then as a statistician would use it.

What effect-size measure is used with two-way ANOVA?

For each of the following scenarios, what are two names for the ANOVA that would be conducted to analyze the data?

Identify the factors and their levels in the following research designs.

State how many cells there should be for each of these studies. Then, create an empty grid to represent those cells.

Use these “enjoyment” data to perform the following:

Use these data—incidents of reports of underage drinking—to perform the following:

“Dry” campus, state school: 47, 52, 27, 50

“Dry” campus, private school: 25, 33, 31

“Wet” campus, state school: 77, 61, 55, 48

“Wet” campus, private school: 52, 68, 60

Using what you know about the expanded source table, fill in the missing values in the table shown here:

Using the information in the source table provided here, compute R² values for each effect. Using Cohen’s conventions, explain what these values mean.

Using the information in the source table provided here, compute R² values for each effect. Using Cohen’s conventions, explain what these values mean.

Football, eye glare, and ANOVA: In Exercise 11.67 (page 322), we described a Yale University study. Let’s consider a redesign in which researchers randomly assigned 46 participants to place one of three substances below their eyes: black grease, black antiglare stickers, or petroleum jelly. They assessed eye glare using a contrast chart that gives a value for each participant, a scale measure. Black grease led to a reduction in glare compared with the two other conditions, antiglare stickers or petroleum jelly (DeBroff & Pahk, 2003). Imagine that every participant was tested twice, once in broad daylight and again under the artificial lights used at night.

Health-related myths and the type of ANOVA: Consider the study we used as an example for a two-way between-groups ANOVA. Older and younger people were randomly assigned to hear either one repetition or three repetitions of a health-related myth, accompanied by the accurate information that “busted” the myth.

Memory and choosing the type of ANOVA: In a fictional study, a cognitive psychologist studied memory for names after a group activity. The researcher randomly assigned 120 participants to one of three conditions: (1) group members introduced themselves once, (2) group members were introduced by the experimenter and by themselves, and (3) group members were introduced by the experimenter and themselves, and they wore name tags throughout the group activity.

Age, online dating, and choosing the type of ANOVA: A researcher wondered about the degree to which age was a factor for those posting personal ads on Match.com. He randomly selected 200 ads and examined data about the posters (the people who posted the ads). Specifically, for each ad, he calculated the difference between the poster’s age and the oldest acceptable age in a romantic prospect. So, if someone were 23 years old and would date someone as old as 30, his or her score would be 7; if someone were 25 and would date someone as old as 23, his or her score would be −2. The researcher then categorized the scores into male versus female and seeking a same-sex date versus seeking an opposite-sex date.

Racism, juries, and interactions: In a study of racism, Nail, Harton, and Decker (2003) had participants read a scenario in which a police officer assaulted a motorist. Half the participants read about an African American officer who assaulted a European American motorist, and half read about a European American officer who assaulted an African American motorist. Participants were categorized based on political orientation: liberal, moderate, or conservative. Participants were told that the officer was acquitted of assault charges in state court but was found guilty of violating the motorist’s rights in federal court. Double jeopardy occurs when an individual is tried twice for the same crime. Participants were asked to rate, on a scale of 1–7, the degree to which the officer had been placed in double jeopardy by the second trial.

The researchers reported the interaction as F(2, 58) = 10.93, p < 0.0001. The means for the liberal participants were 3.18 for those who read about the African American officer and 1.91 for those who read about the European American officer. The means for the moderate participants were 3.50 for those who read about the African American officer and 3.33 for those who read about the European American officer. The means for the conservative participants were 1.25 for those who read about the African American officer and 4.62 for those who read about the European American officer.

Self-interest, ANOVA, and interactions: Ratner and Miller (2001) wondered whether people are uncomfortable when they act in a way that’s not obviously in their own self-interest. They randomly assigned 33 women and 32 men to read a fictional passage saying that federal funding would soon be cut for research into a gastrointestinal illness that mostly affected either (1) women or (2) men. They were then asked to rate, on a 1–7 scale, how comfortable they would be “attending a meeting of concerned citizens who share your position” on this cause (p. 11). A higher rating indicates a greater degree of comfort. The journal article reported the statistics for the interaction as F(1, 58) = 9.83, p < 0.01. Women who read about women had a mean of 4.88, whereas those who read about men had a mean of 3.56. Men who read about women had a mean of 3.29, whereas those who read about men had a mean of 4.67.

Gender, negotiating a salary, and an interaction: Eleanor Barkhorn (2012) reported in the Atlantic about differences in women’s and men’s negotiating styles. She first explained that researchers did not find a significant difference in how likely women and men are to negotiate salaries. But this did not tell the whole story. Barkhorn wrote: “Women are more likely to negotiate when an employer explicitly says that wages are negotiable. Men, on the other hand, are more likely to negotiate when the employer does not directly state that they can negotiate.”

For each of the following, state whether the finding is a result of examining a main effect or examining an interaction. Explain your answer.

The cross-race effect, main effects, and interactions: Hugenberg, Miller, and Claypool (2007) conducted a study to better understand the cross-race effect, in which people have a difficult time recognizing members of different racial groups—colloquially known as the “they all look the same to me” effect. In a variation on this study, white participants viewed either 20 black faces or 20 white faces for 3 seconds each. Half the participants were told to pay particular attention to distinguishing features of the faces. Later, participants were shown 40 black faces or 40 white faces (the same race that they were shown in the prior stage of the experiment), 20 of which were new. Each participant received a score that measured his or her recognition accuracy.

The researchers reported two effects, one for the race of the people in the pictures, F(1, 136) = 23.06, p <0.001, such that white faces were more easily recognized, on average, than black faces. There also was a significant interaction of the race of the people in the pictures and the instructions, F(1, 136) = 5.27, p < 0.05. When given no instructions, the mean recognition scores were 1.46 for white faces and 1.04 for black faces. When given instructions to pay attention to distinguishing features, the mean recognition scores were 1.38 for white faces and 1.23 for black faces.

Grade point average, fraternities, sororities, and two-way between-groups ANOVA: A sample of students from our statistics classes reported their GPAs, indicated their genders, and stated whether they were in the university’s Greek system (i.e., in a fraternity or sorority). Following are the GPAs for the different groups of students:

Men in a fraternity: 2.6, 2.4, 2.9, 3.0

Men not in a fraternity: 3.0, 2.9, 3.4, 3.7, 3.0

Women in a sorority: 3.1, 3.0, 3.2, 2.9

Women not in a sorority: 3.4, 3.0, 3.1, 3.1

Age, online dating, and two-way between-groups ANOVA: The data below were from the same 25-year-old participants described in How It Works 12.1, but now the scores represent the oldest age that would be acceptable in a dating partner.

25-year-old women seeking men: 40, 35, 29, 35, 35

25-year-old men seeking women: 26, 26, 28, 28, 28

25-year-old women seeking women: 35, 35, 30, 35, 45

25-year-old men seeking men: 33, 35, 35, 36, 38

Helping, payment, and two-way between-groups ANOVA: Heyman and Ariely (2004) were interested in whether effort and willingness to help were affected by the form and amount of payment offered in return for effort. They predicted that when money was used as payment, in what is called a money market, effort would increase as a function of payment level. On the other hand, if effort were performed out of altruism, in what is called a social market, the level of effort would be consistently high and unaffected by level of payment. In one of their studies, college students were asked to estimate another student’s willingness to help load a sofa into a van in return for a cash payment or candy of equivalent value. Willingness to help was assessed using an 11-point scale ranging from “Not at all likely to help” to “Will help for sure.” Data are presented here to re-create some of their findings.

Cash payment, low amount of $0.50: 4, 5, 6, 4

Cash payment, moderate amount of $5.00: 7, 8, 8, 7

Candy payment, low amount valued at $0.50: 6, 5, 7, 7

Candy payment, moderate amount valued at $5.00: 8, 6, 5, 5

Helping, payment, and interactions: Expanding on the work of Heyman and Ariely (2004) as described in the previous exercise, let’s assume a higher level of payment was included and the following data were collected. (Notice that all data are the same as earlier, with the addition of new data under a high payment amount.)

Cash payment, low amount of $0.50: 4, 5, 6, 4

Cash payment, moderate amount of $5.00: 7, 8, 8, 7

Cash payment, high amount of $50.00: 9, 8, 7, 8

Candy payment, low amount, valued at $0.50: 6, 5, 7, 7

Candy payment, moderate amount, valued at $5.00: 8, 6, 5, 5

Candy payment, high amount, valued at $50.00: 6, 7, 7, 6

Exercise, well-being, and type of ANOVA: Cox, Thomas, Hinton, and Donahue (2006) studied the effects of exercise on well-being. There were three independent variables: age (18–20 years old, 35–45 years old), intensity of exercise (low, moderate, high), and time point (15, 20, 25, and 30 minutes). The dependent variable was positive well-being. Every participant was assessed at all intensity levels and all time points. (Generally, moderate-intensity exercise and high-intensity exercise led to higher levels of positive well-being than did low-intensity exercise.) What type of ANOVA would the researchers conduct?

Negotiation, an interaction, and a graph: German psychologist David Loschelder and his colleagues conducted an experiment on negotiations (2014). They cited tennis player Andy Roddick’s agent who thought it was always detrimental to make an initial offer, saying “The first offer gives you an insight into their [the other party’s] thought process.” The researchers wondered if this was always true. So, they conducted an experiment with two independent variables. One independent variable was the person’s role in the negotiations—either the person starting the negotiation (the sender) or the person being targeted (the receiver). The second independent variable was the type of information in the initial offer—different or the same. That is, the sender was either asking for something that is different from what the other partner wants or asking for something that the other person also wants. For example, if you are negotiating with a new employer, you might ask for five weeks of vacation and a higher salary than you think you can get. And maybe the employer was already prepared to give you five weeks vacation. So, the researchers thought the type of information that matches what the other person wants (like the information about vacation time) might give the receiver a bargaining chip. Knowing what the sender really wants might let you lowball on other aspects of the negotiation. So, the employer can then grant the vacation time, and perhaps not have to offer the higher salary. The graph here depicts the results of this experiment, in which success in the negotiation was measured in the percentage of a pool of money that could be earned.

361

Skepticism, self-interest, and two-way ANOVA: A study on motivated skepticism examined whether participants were more likely to be skeptical when it served their self-interest (Ditto & Lopez, 1992). Ninety-three participants completed a fictitious medical test that told them they had high levels of a certain enzyme, TAA. Participants were randomly assigned to be told either that high levels of TAA had potentially unhealthy consequences or potentially healthy consequences. They were also randomly assigned to complete a dependent measure before or after the TAA test. The dependent measure assessed their perception of the accuracy of the TAA test on a scale of 1 (very inaccurate) to 9 (very accurate). Ditto and Lopez found the following means for those who completed the dependent measure before taking the TAA test: unhealthy result, 6.6; healthy result, 6.9. They found the following means for those who completed the dependent measure after taking the TAA test: unhealthy result, 5.6; healthy result, 7.3. From their ANOVA, they reported statistics for two findings. For the main effect of test outcome, they reported the following statistic: F(1,73) = 7.74, p < 0.01. For the interaction of test outcome and timing of the dependent measure, they reported the following statistic: F(1, 73) = 4.01, p < 0.05.

Feedback and ANOVA: Stacey Finkelstein and Ayelet Fishbach (2012) examined the impact of feedback in the learning process. The following is an excerpt from their abstract: “This article explores what feedback people seek and respond to. We predict and find a shift from positive to negative feedback as people gain expertise. We document this shift in a variety of domains, including feedback on language acquisition, pursuit of environmental causes, and use of consumer products. Across these domains, novices sought and responded to positive feedback, and experts sought and responded to negative feedback” (p. 22).
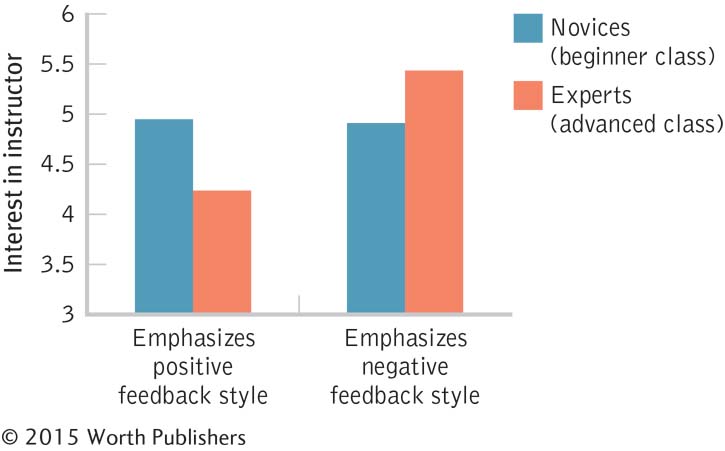