nolanessentials3e

Inferential Statistics

In Chapter 1, we introduced the two main branches of statistics—descriptive statistics and inferential statistics. The link that connects the two branches is probability. Descriptive statistics allow us to summarize characteristics of the sample, but we must use probability with inferential statistics when we apply what we’ve learned from the sample, such as in an exit poll, to the larger population. Inferential statistics, also referred to as hypothesis testing, helps us to determine the probability of a given outcome.

Developing Hypotheses

We informally develop and test hypotheses all the time. I hypothesize that the traffic will be heavy on Western Avenue, so I take a parallel street to work and keep looking down each block to see if my hypothesis is being supported. In a science blog, TierneyLab, reporter John Tierney and his collaborators asked people to estimate the number of calories in a meal pictured in a photograph (Tierney, 2008a, 2008b). One group was shown a photo of an Applebee’s Oriental Chicken Salad and a Pepsi. Another group was shown a photo of the same salad and Pepsi, but it also included a third item—Fortt’s crackers, with a label that clearly stated “Trans Fat Free.” The researchers hypothesized that the addition of the “healthy” food item would affect people’s calorie estimates of the entire meal. They tested a sample and used probability to apply their findings from the sample to the population.

Using a Sample to Make Probability-Based Judgments About the Population Does the presence of a low-calorie item, such as a diet soda, make a higher-calorie item, such as french fries, seem healthier? Researchers use samples to test hypotheses such as this about a population.

110

Let’s put this study in the language of sampling and probability. The sample was comprised of people living in the Park Slope neighborhood of Brooklyn in New York City, an area that Tierney terms “nutritionally correct” because of the abundance of organic food in local stores. The population would include all the residents of Park Slope who could have been part of this study. The driving concern behind this research was the increasing levels of obesity in many wealthier countries (something that Tierney explored in a follow-up study). For now, however, we can only infer that the results may apply to the residents of Park Slope and similar neighborhoods. The independent variable in this case is the presence or absence of the healthy crackers in the photo of the meal. The dependent variable is the number of calories estimated.

A control group is a level of the independent variable that does not receive the treatment of interest in a study. It is designed to match an experimental group in all ways but the experimental manipulation itself.

An experimental group is a level of the independent variable that receives the treatment or intervention of interest in an experiment.

The group that viewed the photo without the healthy crackers is the control group, a level of the independent variable that does not receive the treatment of interest in a study. It is designed to match the experimental group—a level of the independent variable that receives the treatment or intervention of interest—in all ways but the experimental manipulation itself. In this example, the experimental group would be those viewing the photo that included the healthy crackers.

MASTERING THE CONCEPT

5-5: Many experiments have an experimental group in which participants receive the treatment or intervention of interest, and a control group in which participants do not receive the treatment or intervention of interest. Aside from the intervention with the experimental group, the two groups are treated identically.

The null hypothesis is a statement that postulates that there is no difference between populations or that the difference is in a direction opposite of that anticipated by the researcher.

The next step is the development of the hypotheses to be tested. Ideally, this is done before the data from the sample are actually collected; you will see this pattern of developing hypotheses and then collecting data repeated throughout this book. When we calculate inferential statistics, we’re actually comparing two hypotheses. One is the null hypothesis—a statement that postulates that there is no difference between populations or that the difference is in a direction opposite to that anticipated by the researcher. In most circumstances, we can think of the null hypothesis as the boring hypothesis because it proposes that nothing will happen. In the healthy food study, the null hypothesis is that the average (mean) calorie estimate is the same for both populations, which are comprised of all the people in Park Slope who either view or do not view the photo with the healthy crackers.

The research hypothesis is a statement that postulates that there is a difference between populations or sometimes, more specifically, that there is a difference in a certain direction, positive or negative; also called an alternative hypothesis.

MASTERING THE CONCEPT

5-6: Hypothesis testing allows us to examine two competing hypotheses. The first, the null hypothesis, posits that there is no difference between populations or that any difference is in the opposite direction from what is predicted. The second, the research hypothesis, posits that there is a difference between populations (or that the difference between populations is in a predicted direction—either higher or lower).

In contrast to the null hypothesis, the research hypothesis is usually the exciting hypothesis. The research hypothesis (also called the alternative hypothesis) is a statement that postulates a difference between populations. In the healthy food study, the research hypothesis would be that, on average, the calorie estimate is different for those viewing the photo with the healthy crackers than for those viewing the photo without the healthy crackers. It also could specify a direction—that the mean calorie estimate is higher (or lower) for those viewing the photo with the healthy crackers than for those viewing the photo with just the salad and Pepsi. Notice that, for all hypotheses, we are very careful to state the comparison group. We do not say merely that the group viewing the photo with the healthy crackers has a higher (or lower) average calorie estimate. We say that it has a higher (or lower) average calorie estimate than the group that views the photo without the healthy crackers.

We formulate the null hypothesis and research hypothesis to set them up against each other. We use statistics to determine the probability that there is a large enough difference between the means of the samples that we can conclude there’s likely a difference between the means of the underlying populations. So, probability plays into the decision we make about the hypotheses.

Making a Decision About the Hypothesis

111

When we make a conclusion at the end of a study, the data lead us to conclude one of two things:

We decide to reject the null hypothesis.
We decide to fail to reject the null hypothesis.

We always begin our reasoning about the outcome of an experiment by reminding ourselves that we are testing the (boring) null hypothesis. In terms of the healthy food study, the null hypothesis is that there is no mean difference between groups. In hypothesis testing, we determine the probability that we would see a difference between the means of the samples, given that there is no actual difference between the underlying population means.

EXAMPLE 5.2

After we analyze the data, we do one of two things:

Reject the null hypothesis. “I reject the idea that there is no mean difference between populations.” When we reject the null hypothesis that there is no mean difference, we can even assert what we believe the difference to be, based on the actual findings. We can say that it seems that people who view a photo of a salad, Pepsi, and healthy crackers estimate a lower (or higher, depending on what we found in our study) number of calories, on average, than those who view a photo with only the salad and Pepsi.
Fail to reject the null hypothesis. “I do not reject the idea that there is no mean difference between populations.” In this case, we can only say that we do not have evidence to support our hypothesis.

Let’s take the first possible conclusion, to reject the null hypothesis. If the group that viewed the photo that included the healthy crackers has a mean calorie estimate that is a good deal higher (or lower) than the control group’s mean calorie estimate, then we might be tempted to say that we accept the research hypothesis that there is such a mean difference in the populations—that the addition of the healthy crackers makes a difference. Probability plays a central role in determining that the mean difference is large enough that we’re willing to say it’s real. But rather than accept the research hypothesis in this case, we reject the null hypothesis, the one that suggests there is nothing going on. We repeat: When the data suggest that there is a mean difference, we reject the idea that there is no mean difference.

The second possible conclusion is failing to reject the null hypothesis. There’s a very good reason for thinking about this in terms of failing to reject the null hypothesis rather than accepting the null hypothesis. Let’s say there’s a small mean difference, and we conclude that we cannot reject the null hypothesis (remember, rejecting the null hypothesis is what we want to do!). We determine that it’s just not likely enough—or probable enough—that the difference between means is real. It could be that a real difference between means didn’t show up in this particular sample just by chance. There are many ways in which a real mean difference in the population might not get picked up by a sample. We repeat: When the data do not suggest a difference, we fail to reject the null hypothesis, which is that there is no mean difference.

The way we decide whether to reject the null hypothesis is based directly on probability. We calculate the probability that the data would produce a difference between means this large and in a sample of this size if there was nothing going on.

112

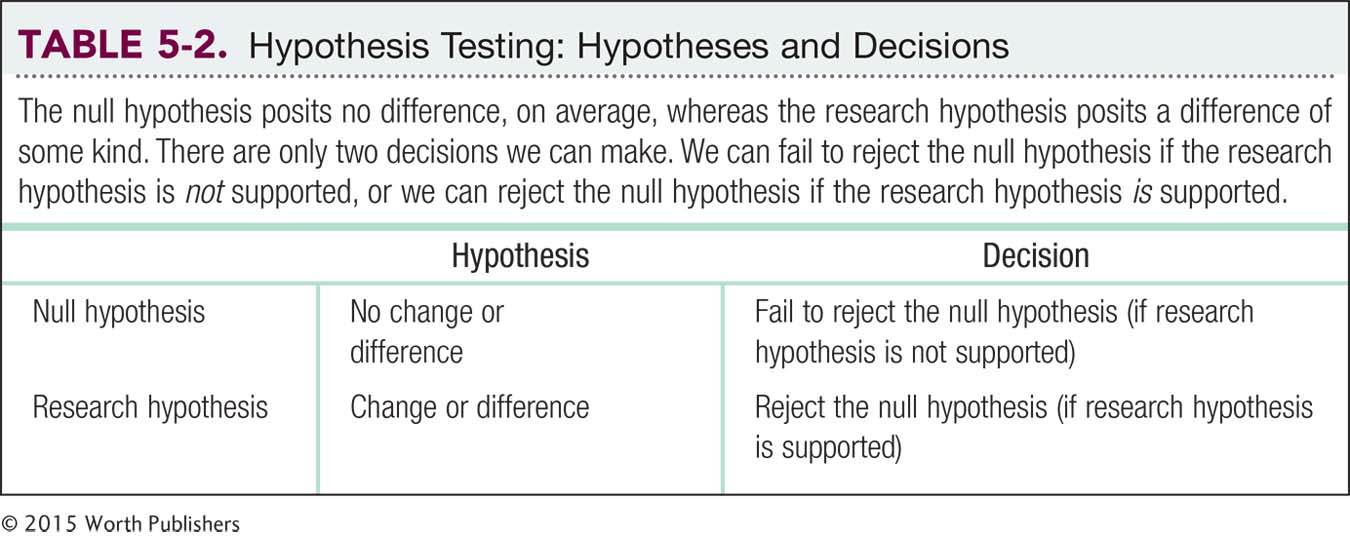
We will be giving you many more opportunities to get comfortable with the logic of formal hypothesis testing before we start applying numbers to it, but here are three easy rules and a table (Table 5-2) that will help keep you on track.

Remember: The null hypothesis is that there is no difference between groups, and usually the hypotheses explore the possibility of a mean difference.
We either reject or fail to reject the null hypothesis. There are no other options.
We never use the word accept in reference to formal hypothesis testing.

Hypothesis testing is exciting when you care about the results. You may wonder what happened in Tierney’s study. Well, people who saw the photo with just the salad and the Pepsi estimated, on average, that the 934-calorie meal contained 1011 calories. When the 100-calorie crackers were added, the meal actually increased from 934 calories to 1034 calories; however, those who viewed this photo estimated, on average, that the meal contained only 835 calories! Tierney referred to this effect as “a health halo that magically subtracted calories from the rest of the meal.” Interestingly, he replicated this study with mostly foreign tourists in New York’s Times Square and did not find this effect. He concluded that health-conscious people like those living in Park Slope were more susceptible to the magical health halo bias than were other people.

CHECK YOUR LEARNING

Reviewing the Concepts		In experiments, we typically compare the average of the responses of those who receive the treatment or manipulation (the experimental group) with the average of the responses of similar people who do not receive the manipulation (the control group). Researchers develop two hypotheses: a null hypothesis, which theorizes that there is no average difference between levels of an independent variable in the population, and a research hypothesis, which theorizes that there is an average difference of some kind in the population. Researchers can draw two conclusions: They can reject the null hypothesis and conclude that they have supported the research hypothesis or they can fail to reject the null hypothesis and conclude that they have not supported the research hypothesis.
Clarifying the Concepts	5-8	At the end of a study, what does it mean to reject the null hypothesis?
Calculating the Statistics	5-9	State the difference that might be expected, based on the null hypothesis, between the average test grades of students who attend review sessions versus those who do not.
Applying the Concepts	5-10	A university lowers the heat during the winter to save money, and professors wonder whether students will perform more poorly, on average, under cold conditions. Cite the likely null hypothesis for this study. Cite the likely research hypothesis. If the cold temperature appears to decrease academic performance, on average, what will the researchers conclude in terms of formal hypothesis-testing language? If the researchers do not gather sufficient evidence to conclude that the cold temperature leads to decreased academic performance, on average, what will they conclude in terms of formal hypothesis-testing language?

Solutions to these Check Your Learning questions can be found in Appendix D.

113