nolanessentials3e

Type I and Type II Errors

Wrong decisions can be the result of unrepresentative samples. However, even when sampling has been properly conducted, there are still two ways to make a wrong decision: 1) We can reject the null hypothesis when we should not have rejected it, or 2) we can fail to reject the null hypothesis when we should have rejected it. So let’s consider the two types of errors using statistical language.

Type I Errors

A Type I error involves rejecting the null hypothesis when the null hypothesis is correct.

Type I and Type II Errors The results of a home pregnancy test are either positive (indicating pregnancy) or negative (indicating no pregnancy). If the test is positive, but the woman is not pregnant, this would be a Type I error. If the test is negative, but the woman is pregnant, this would be a Type II error. With pregnancy tests, as with hypothesis testing, people are more likely to act on a Type I error than on a Type II error. In the photo, the line on the left is lighter than the line on the right, so the pregnancy test seems to indicate that this woman is pregnant, which could be a Type I error.

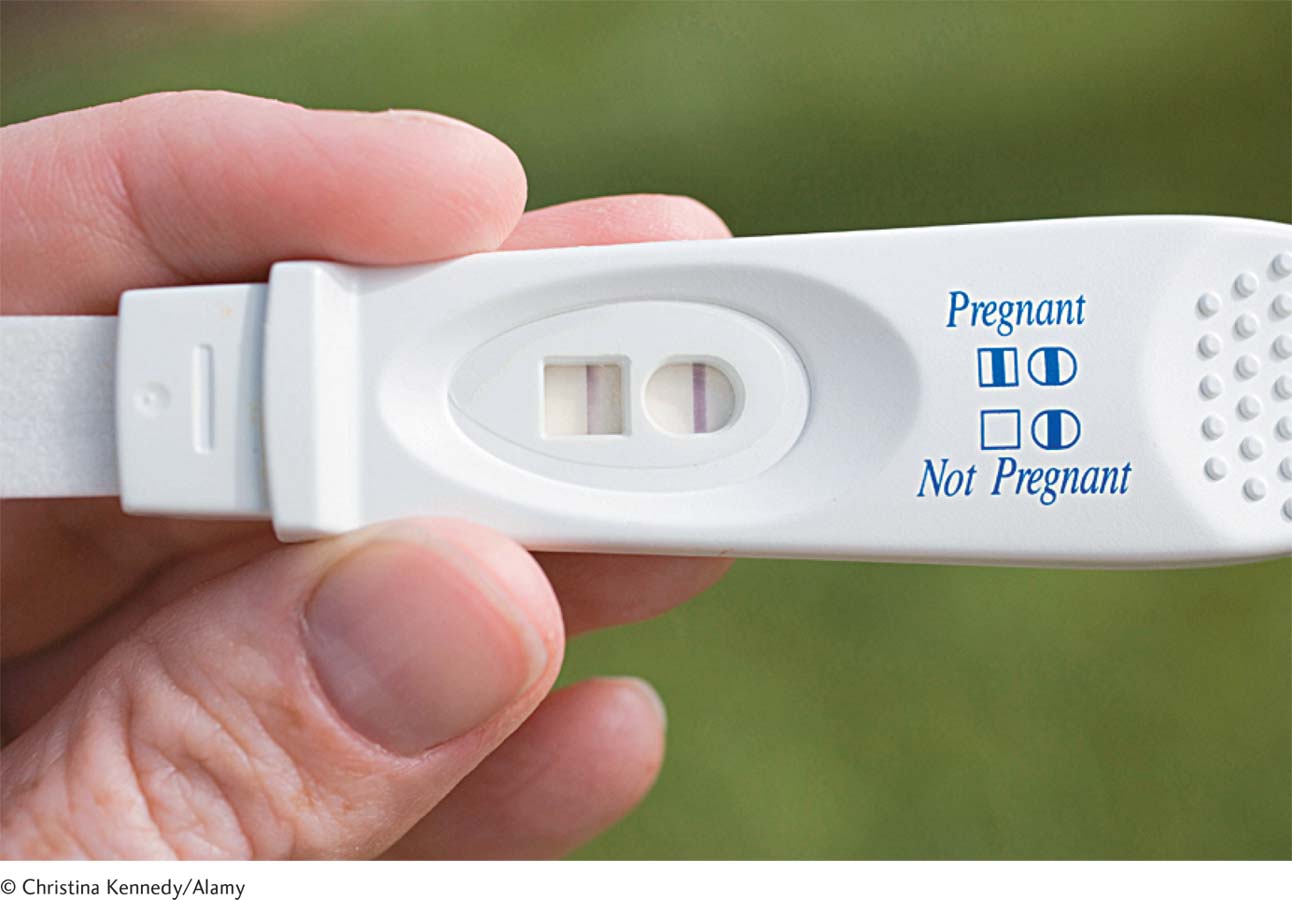
If we reject the null hypothesis, but it was a mistake to do so, then we have made a Type I error. Specifically, we commit a Type I error when we reject the null hypothesis but the null hypothesis is correct. A Type I error is like a false positive in a medical test. For example, if a woman believes she might be pregnant, then she might buy a home pregnancy test. In this case, the null hypothesis would be that she is not pregnant, and the research hypothesis would be that she is pregnant. If the test is positive, the woman rejects the null hypothesis—the one in which she theorizes that she is not pregnant. Based on the test, the woman believes she is pregnant. Pregnancy tests, however, are not perfect. If the woman tests positive and rejects the null hypothesis, it is possible that she is wrong and it is a false positive. Based on the test, the woman believes she is pregnant even though she is not pregnant. A false positive is equivalent to a Type I error.

A Type I error indicates that we rejected the null hypothesis falsely. As you might imagine, the rejection of the null hypothesis typically leads to action, at least until we discover that it is an error. For example, the woman with a false-positive pregnancy test might announce the news to her family and start buying baby clothes. Many researchers consider the consequences of a Type I error to be particularly detrimental because people often take action based on a mistaken finding.

Type II Errors

A Type II error involves failing to reject the null hypothesis when the null hypothesis is false.

114

MASTERING THE CONCEPT

5-7: In hypothesis testing, there are two types of errors that we risk making. Type I errors, in which we reject the null hypothesis when the null hypothesis is true, are like false positives on a medical test; we think someone has a disease, but they really don’t. Type II errors, in which we fail to reject the null hypothesis when the null hypothesis is not true, are like false negatives on a medical test; we think someone does not have a disease, but they really do.

If we fail to reject the null hypothesis but it was a mistake to fail to do so, then we have made a Type II error. Specifically, we commit a Type II error when we fail to reject the null hypothesis but the null hypothesis is false. A Type II error is like a false negative in medical testing. In the pregnancy example earlier, the woman might get a negative result on the test and fail to reject the null hypothesis, the one that says she’s not pregnant. In this case, she would conclude that she’s not pregnant when she really is. A false negative is equivalent to a Type II error.

We commit a Type II error when we incorrectly fail to reject the null hypothesis. A failure to reject the null hypothesis typically results in a failure to take action—for instance, a research intervention is not performed or a diagnosis is not given—which is generally less dangerous than incorrectly rejecting the null hypothesis. Yet there are cases in which a Type II error can have serious consequences. For example, the pregnant woman who does not believe she is pregnant because of a Type II error may drink alcohol in a way that unintentionally harms her fetus.

CHECK YOUR LEARNING

Reviewing the Concepts		When we draw a conclusion from inferential statistics, there is always a chance that we are wrong. When we reject the null hypothesis, but the null hypothesis is true, we have committed a Type I error. When we fail to reject the null hypothesis, but the null hypothesis is not true, we have committed a Type II error.
Clarifying the Concepts	5-11	Explain how Type I and Type II errors both relate to the null hypothesis.
Calculating the Statistics	5-12	If 7 out of every 280 people in prison are innocent, what is the rate of Type I errors?
	5-13	If the court system fails to convict 11 out of every 35 guilty people, what is the rate of Type II errors?
Applying the Concepts	5-14	Researchers conduct a study on perception by having participants throw a ball at a target first while wearing virtual-reality glasses and then while wearing glasses that allow normal viewing. The null hypothesis is that there is no difference in performance when wearing the virtual-reality glasses versus when wearing the glasses that allow normal viewing. The researchers reject the null hypothesis, concluding that the virtual-reality glasses lead to a worse performance than do the normal glasses. What error might the researchers have made? Explain. The researchers fail to reject the null hypothesis, concluding that it is possible that the virtual-reality glasses have no effect on performance. What error might the researchers have made? Explain.

Solutions to these Check Your Learning questions can be found in Appendix D.